한담객설 2015년 11월 29일 <목 차> I. 청천낙성 우리 존재의 위치 찾기 (5)
(1) 구상성단 안시밝기를 이용한 거리측정이 가능할까 ? (2) 구상성단 안시밝기 통계 만들 때 필요한 사항 1. 가우스 절대값 및 가우스 함수 2. 정규분포그래프 해석방법 예시 (3) 우리은하 및 M31 구상성단 광도그래프 그리기 1. 각 은하내부 구상성단
갯수 2. 구상성단 광도함수 (4) 구상성단 안시밝기 광도함수로 거리 계산하기 1. NGC
4494 2. NGC
4565 (5) 구상성단 광도함수 적용가능 한계거리 (6)
Face-On, Edge-On 나선은하의 구상성단 (7) 타원은하의 구상성단 (8) 아이디어의 Shapley, 액션의 Baum
II. 담천잡담 다른 문화 다른 별자리
(5) – 북극권 원주민의 Orion Belt (1) 북극권이란 ? (2) 헷갈리는
북극권의 낮과 밤 (3) 원인은
지구자전축 기울기 (4) 북극권
경계선에 서서 1. 하지의
태양궤적 2. 동지의
태양궤적 (5) 단순명쾌한 Inuit 전설
III. 월하산책 잃어버린
별자리를 찾아서 (22) – 작은삼각형 Triangulum Minus
(1) 작은삼각형 – 나
만든 사람 나와 봐 ! (2) 삼각형 – 내 나이는 2,300 살
(3) 남쪽삼각형
– 아빠 찾아 삼만리
<본 문> I. 청천낙성 우리
존재의 위치 찾기 (5)
(1) 구상성단 안시밝기를 이용한 거리측정이 가능할까 ? 지난 8월 이후로 5 개월 동안이나 계속 “거리” 운운하고 있습니다. 한가지 소재로 지루하게 시간을 너무 끄는 것 같습니다. 그렇더라도 이번 기회에 우주거리 측정방법에
대해 가능한한 다양하고 정확하게 살펴본다고 생각해 주시면 감사하겠습니다. 여기서도 거리계산식은 지난 8월 16일자 내용에 따르겠습니다. 또한 이 칼럼에 표기된 모든 거리는 우주팽창이 감안된 Light Travel Distance 입니다. 이번에
알아볼 내용은 “구상성단 (Globular Cluster)” 을
이용한 방법입니다. 지난 한담객설 8월 30일자에선 Harlow
Shapley (할로우 섀플리 1885~1972. 미국)
가 우리은하 내부 75 개 구상성단까지 거리를 쟀다고 말씀 드렸습니다. 당시 사용된 방법은 구상성단에 존재하는
Cepheid 변광 성 중에서 특히 RR Lyrae 변광성을
이용한 방법이었습니다. 그러나
이번에 말씀드리는 방법은 “구상성단 자체의 안시밝기 (B. Apparent Brightness)” 를 이용합니다. 거리측정의
기본사항은 그 대상까지의 본래광도 (L. Intrinsic Luminosity) 를 알아내는 것입니다. 우선 여러가지 은하내부의 구상성단 자체
안시밝기 (B) 를 측정해서 통계를 낸 다음, 그 통계들에서
특정한 규칙성을 도출합니다. 그
규칙성이 이미 거리를 알고 있는 어떤 은하내부 구상성단에도 적용가능하다면, 해당 규칙성으로부터 거리를
측정하려는 구상성단의 본래광도 (L) 를 알 수 있게되어 거리를 계산할 수 있습니다. 그런데
구상성단의 지름은 보통 150~200 광년이고, 그 내부
별들 갯수는 대략 1,000~1,500 만개 정도입니다. 발견된 구상성단 중에서 직경이 가장 크다고 알려진 NGC 2419 (Hercules 자리) 직경은 무려 260 광년이나 되므로, 비례적으로 계산한다면 그 내부엔 3,000 만개 이상 별들이 존재합니다 (구체의 부피는 반지름의 세제곱에
비례. V = 4/3 π r 3 승수). 별이 많은
구상성단은 별이 적은 구상성단보다 본래광도가 당연히 더 클 것입니다. 이렇게 본래광도가 천차만별인 구상성단들의 안시밝기도 제각각일텐데, 거기서 어떻게 규칙성을 찾아내고 거리를 계산할 수 있을까요 ? (2) 구상성단 안시밝기 통계 만들 때 필요한 사항 1. 가우스 절대값 및
가우스 함수 서로 다른
형태를 가진 구성요소들의 전체적 형태를 파악할 때는 통계가 사용됩니다. 구상성단으로 거리를 측정하는 방법도 기본적으론 Cepheid 변광성을 이용한 방법 또는 Tully-Fisher 통계와
동일한 경험적, 통계적 방법입니다. 그런데 구상성단들 안시밝기로 통계를 낼 때는 통계에 관련된 몇가지 기법이
필요합니다. 구상성단의
안시밝기 (또는 안시등급) 단위를 가우스 (Gauss) 절대값을 사용해서 표시하고, 도출된 그래프를 분석하면
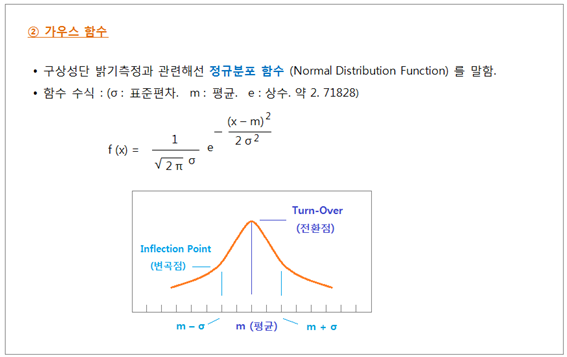
가우스 함수를 이용한 정규분포 곡선으로 나타납니다. 가우스 절대값 및 가우스 함수는 예전에 배웠다고 어렴풋이 기억됩니다. 모르셔도 지장없으나, 아래 단락들에서 이들 용어를 사용해야하므로 내용을 간단히 정리해 보았습니다. 수식은 참고만 하시면 되며, “정규분포그래프
모양” 과 “평균의 위치”
를 보시기 바랍니다. <그림 1/2 가우스 절대값 및 가우스 함수> 정규분포그래프에선 y 축 값이 가장 커지는 전환점 (Turn-Over) 이 x 축 값의 평균 (m) 이 됩니다. 따라서 어떤 분포도가 정규분포 곡선을 이루고 있으면, x 축 값의 평균은 항상 산 (山) 모양 꼭대기 (頂點) 지점입니다. 표준편차
σ (시그마) 는
y 축 값이 x 축 평균
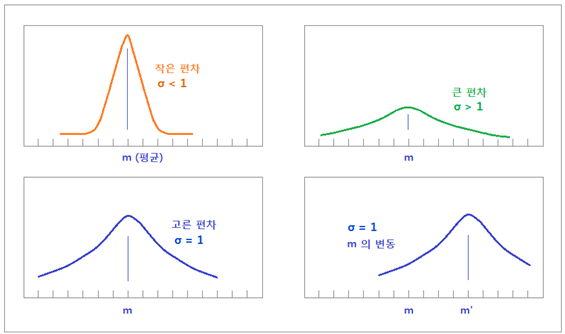
(m) 에 얼마나 집중되어있는지 나타냅니다. y 축 값이 x 축 평균 (m) 에 많이 집중되어 있다면 뾰족한 산이 될 겁니다. 이 경우는 “편차가 작다” 라고 표현되며, 표준편차 σ 가 1 보다
작을 때입니다. 반대로 평균에서
산만하게 퍼져 있다면 “편차가 크다” 라고 표현되고, 표준편차 σ 는 1 보다 큽니다. 표준편차 σ 가 1 일때는
y 축 값이 x 축 값 평균을 중심으로 “고르게 분포” 되어 있는 상태입니다.
<그림 3 표준편차 σ 크기에 따른 정규분포 그래프 변화> 2. 정규분포그래프 해석방법
예시 가우스
절대값을 사용해서 만든 통계가 가우스 함수인 정규분포 그래프가 될 경우에, 해당 그래프를 해석하는 방법에
대한 예를 들어 보겠습니다. 서울의
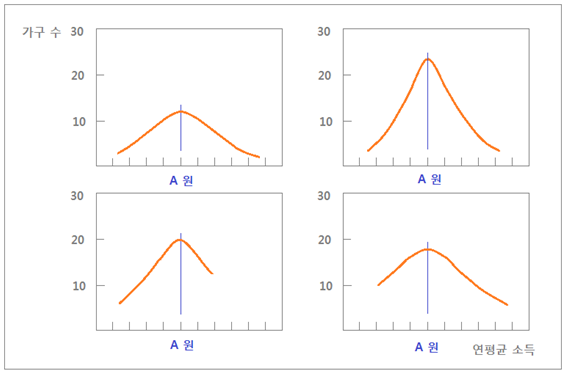
여러 개 동을 무작위 추출해서 가구별 연 (年) 소득을 그래프로 그린다고 가정해 봅니다. 여기서 연 소득을 가우스 절대값처럼 1 만원이하 소숫점은 절사한다고 생각해 보겠습니다. 그러면 1. 3 만원은 1 만원이 되고, 1. 9 만원도
1 만원이 됩니다. 이런
분류로 만들어진 Histogram 을 연결한 그래프가 산 (山) 모양의 정규분포가 되었다고 가정해 보겠습니다. <그림 4 네 개 동 (洞) 의 연평균 소득과 가구 수 그래프 예시>
위쪽 두
개 동은 저소득부터 고소득 가구들이 고르게 분포하지만, 오른쪽 동이 평균소득 A 원에 더 많은 가구들이 집중되어 있을을 나타냅니다. 아래 왼쪽은 고소득 가구가 없는 동이며,
오른쪽은 저소득 가구가 없습니다. 그러나 네 개 동 모두 A 원에서
곡선의 전환점 (Turn-Over) 을 보입니다. 아래쪽
두 개동은 고소득과 저소득층이 없어 평균에 다소 차이가 있겠지만, 네 개 동 전부를 대상으로 한다면, 네 개동 모든 가구들의 평균소득은 A 원이라고 할 수 있습니다. 따라서 어떤 동 전체가구들의 연평균 소득을
구하려면, (해당 동 내부 전체 가구숫자 x A 원) 으로 계산하면 될 겁니다. (3) 우리은하 및 M31 구상성단 광도그래프 그리기 1. 각 은하내부 구상성단
갯수 그러면
우리은하와 M31 (Andromeda 은하) 내부 구상성단
그래프는 어떻게 그려지는지 살펴보겠습니다. 우선 이들 은하 내부에는 구상성단이 과연 몇 개나 살고 있는지
알아야 그래프를 보아도 감이 잡힐 것 같습니다.
우리은하는 우리 동네이니 당연히 정확히 알면 좋고, M31 도 조만간 40 억년 후부터는 우리은하와 합쳐질 것이므로 같이 알아봅니다. <그림 5 우리은하 내부의 확인된 구상성단 갯수. 출처 : SEDS 웹사이트. 논문주소 : spider.seds.org/spider/MWGC/mwgc.html> <그림 6 M31 내부의 확인된 구상성단 갯수. 출처 : 미국천문학회
(American Astronomical Society) 발행 The Astronomical
Journal. July. 2001. 논문주소 : iopscience.iop.org/article/10.1086/323457/pdf>
두가지
인용문 보시면 우리은하엔 최소 157 개, M31 에는 460 ± 70 개 정도가 있다고
합니다. 각 논문은 2011 년과 2001 년에 작성되었지만, 2015 년 현재까지 이 수치에는 변동없는 것으로 보입니다. 지난 한담객설 8월 30일자에서 우리은하 구상성단 갯수를 최소 158 개로 말씀 드렸으나 157 개로 수정해 놓았습니다. 2. 구상성단 광도함수
이젠 각
은하에 존재하는 모든 구상성단의 안시밝기 (또는 안시등급) 를
측정합니다. 우리은하 내부 모든
구상성단까지 거리는 이미 측정되었으므로 이를 거리관계식에 적용하면 절대등급을 알 수 있습니다. 한편 M31 까지 거리도 이미
알고 있고, 그 내부에 있는 구상성단까지 거리는 모두 같다고 전제하면
M31 내부 구상성단의 절대등급도 구할 수 있습니다. 이들을
가우스 절대값을 이용한 Histogram 으로 나타내고, 그것을
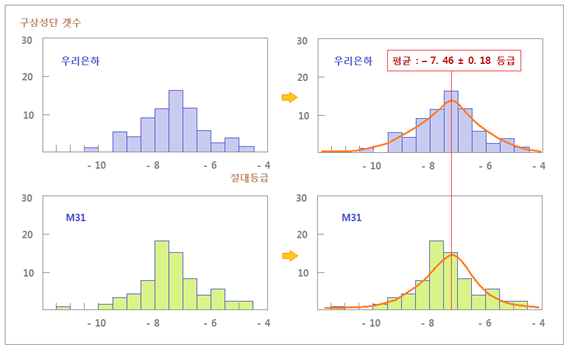
다시 가우스 함수를 이용한 정규분포 그래프로 나타낸 것이 아래 그림입니다. <그림 7 우리은하와 M31 구상성단 광도함수. 아래 출처내용으로 다시 그림. 출처 : NASA/IPAC Extragalactic
Database. 주소
: ned.ipac.caltech.edu. Cornell University Library. 주소 : arxiv.org/abs/1201.3936 등> 오른쪽
두 가지 그림을 보시면 그래프는 정규분포 곡선이 되며, 전환점
(Turn-Over, TO) 에서의 절대등급은 “– 7. 46 ± 0. 18” 이라고 합니다. 자료에 따라 조금씩 차이는 있으나, 오차범위를
포함하면 모두 거의 비슷한 수치가 됩니다.
이 수치를 간단히 – 7. 50 등급으로 표현하기도 합니다. 위 단락에서 말씀드린 것처럼, 이 절대등급이 바로 우리은하와 M31 내부 구상성단들의 “평균 절대등급” 입니다. 또한 이
곡선의 표준편차 (σ) 는 대략 1. 4 정도 입니다. <그림 2> 의 정규분포
함수를 적용하면, 절대등급을 x 축으로하고 구상성단 갯수를
y 축으로한 정규분포 곡선을 그릴 수 있게 됩니다. 거리가 알려진 여러가지 은하내부 구상성단들로 통계를 만든 결과, 모두 유사한 형태를 보였습니다. 따라서 이 광도함수를 다른 은하내부의 구상성단에도 적용할 수 있다는 논리가
성립됩니다. 이런 정규분포
함수를 “구상성단 광도함수 (GCLF / Globular
Cluster Luminosity Function)” 로 부릅니다. 함수란 용어가 들어가서 머리 아프게 생각됩니다만, 단순한 정규분포 그래프를 뜻하므로 용어에 신경쓰지 않으셔도 되리라 생각합니다.
(4) 구상성단 안시밝기 광도함수로 거리 계산하기 1. NGC 4494
아직 거리를
모르는 은하의 구상성단들은 안시밝기 (B 또는 안시등급) 만
알 수 있습니다. 그러나 절대등급
차이는 안시등급 차이와 동일합니다 (1 등급 차이 = 2. 512 배). 또한 구상성단 광도함수의 절대등급 평균이
– 7. 46 ± 0. 18 이므로 이들 안시등급과 절대등급으로 거리를 계산할 수 있습니다. NGC 4494 및 NGC 4565 두가지
은하의 예를 들어 보겠습니다. 절대등급은
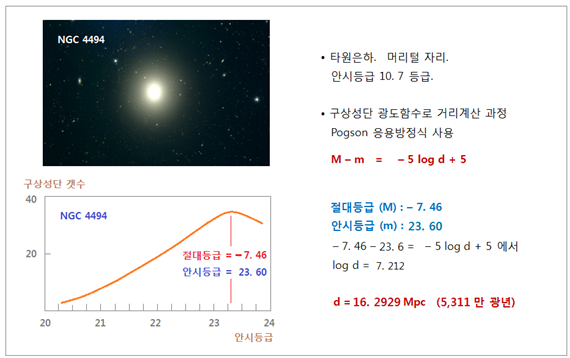
– 7. 46 등급으로 고정하고 계산합니다. <그림 8 NGC 4494 내부 구상성단 광도함수를 이용한 거리계산 과정. 그래프 출처 : Rochester Institute of Technology 내용 참고해서 다시 그림. 주소 : spiff.rit.edu/classes>
NGC 4494 는 머리털자리 (Coma Berenices) 에 있는 타원은하이며, 은하자체의 안시등급은 10. 7 등급입니다. 이 은하내부에 존재하는 구상성단들 안시등급은
20~24 등급 사이 입니다. 이들로 그래프를 만들면 정규분포 곡선이 됩니다. 인용 그래프 출처에 따르면, 안시등급 23. 60 에서 전환점 (Turn-Over. TO) 을 나타낸다고
합니다. 이는 23. 60 등급이 NGC 4494 내부 구상성단들의 “평균 안시등급” 이고, 23. 60
안시등급을 보이는 특정 구상성단의 절대등급이 바로 – 7. 46 ± 0. 18 사이가 됨을 뜻합니다.
절대등급을 – 7. 46 으로
고정해서 계산하면 16. 2929 Mpc (5,311 만 광년) 이
나옵니다. 그래프를
참조한 출처에는 평균 안시등급 수치만 제시되어있고, 거리는 계산되어 있지 않습니다. 산출된
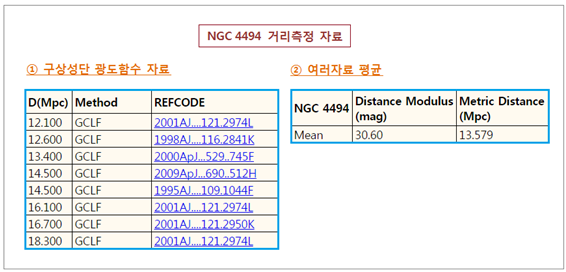
수치가 과연 어느정도 실제와 가까운지, 신뢰할 수 있는 자료를 다시 찾아 보았습니다. <그림 9 NGC 4494 거리측정 자료. 출처 :
NASA/IPAC Extragalactic Database. 주소 : ned.ipac.caltech.edu 그림에
표기된 수치들은 NASA/IPAC Extragalactic Database 에서 인용한 것입니다. 왼쪽 도표는 여러 방법으로 산출된 NGC 4494 까지 거리 중에서, 구상성단 광도함수 (GCLF) 방법으로 계산된 것들입니다. 결과는 12. 10~18. 30 Mpc 사이입니다. 일단 계산결과가 16. 2929 Mpc 이므로 다른 학자들이 계산한 범위 안에는 들어갑니다. 오른쪽
도표는 여러 방법으로 측정된 거리의 평균수치이며 13. 579 Mpc 라고 합니다. 이 거리가 가장 신뢰할 수 있는 수치가
될 겁니다. 인용 그래프로 계산한
거리는 16. 2929 Mpc 이므로, NASA/IPAC
Database 평균수치 13. 579 Mpc 에서 16.
6 % 더 멀게 나왔습니다. 참고로
오른쪽 도표에서 Distance modulus (거리지수) 는 Pogson 응용방정식 (M – m = – 5 log d + 5) 에서 M –
m 을 이항한 m – M 을 뜻합니다. 위의 NGC 4494 그래프
계산방법에 따르면, 거리지수 m – M = 23. 60 – (– 7.
46) = 31. 06 이 됩니다. 2. NGC 4565
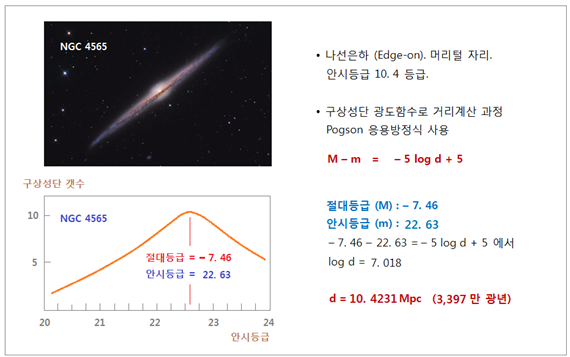
NGC 4565 도 머리털자리에 있습니다. 이 은하는 지구 시선방향에선 은하테두리 부분만 보입니다. 이렇게 은하의 옆면, 테두리만 보이는 은하를 “Edge-On (엣지 온) 은하” 라고 합니다. 이것은 나선은하로 추정되지만,
Edge-On 은하이므로 보이는 모양대로 바늘은하 (Needle Galaxy)로도 불립니다. 인용 그래프 출처에 따르면, 안시등급 23. 63 에서 전환점
(Turn-Over. TO) 을 나타낸다고 합니다. 거리계산 방법은 위의 NGC 4494 와
같습니다. <그림 10 NGC 4565 내부 구상성단 광도함수를 이용한 거리계산 과정. 그래프 출처 : 그림 8
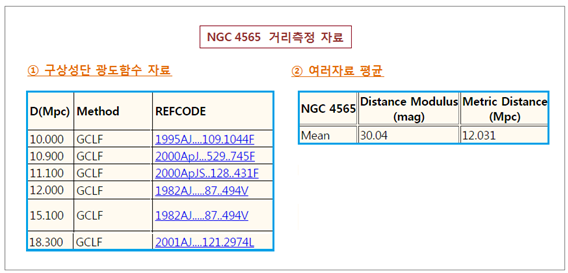
과 동일> <그림 11 NGC 4565 거리측정 자료. 자료출처 : 그림 9 와 동일> 그래프를
토대로 계산한 NGC 4565 까지 거리는 10. 4231 Mpc
(3,397 만 광년) 입니다. 이 결과도 같은 방법으로 다른 학자들이 계산한 10. 00~18.30 Mpc 범위 안에는 들어갑니다. NASA/IPAC Database 평균수치는 12. 031 Mpc (3,922 만 광년) 이므로 13. 3 % 모자라는 결과입니다. (5) 구상성단 광도함수 적용가능 한계거리 연필에는
심의 굵기, 색깔 및 부드러운 정도에 따라 헤아릴 수도 없을만큼 많은 종류가 있고, 부엌칼에도 야채용, 육류용, 생선용, 과일용 등 모양이 여러 종류가 있습니다. 이렇게 모든 도구마다 종류가 많은 이유는 한가지 도구를 여러 목표물에
대해 사용하기엔 한계가 있기 때문입니다. 구상성단
안시밝기 광도함수 방법도 우주의 모든 구상성단에 적용할 수는 없습니다. 이 단락에서는 이 방법의 대표적 한계점을 찾아 보겠습니다. 우선 어떤 은하에 존재하는
구상성단이 안시밝기가 측정될 만큼은 밝아야 할 겁니다. 은하가 너무 멀리 있어서 은하 구성원이 분해도 안되고, 분해가 되더라도 구상성단임을 확인할 수 없다면 이 방법을 적용할 순 없습니다. 그러면 현재까지 구상성단임이 확인되고,
안시밝기가 측정된 것 중, 가장 어두웠던 구상성단 안시등급은 얼마나 될까요 ? 찾아본 자료 중에선 1995 년에 Hubble 망원경이 측정한 NGC 4881 내부 구상성단의 27. 6 등급이 가장 어두운 구상성단이었습니다. 한편, 구상성단 광도함수로 거리를 재려면, 전환점 (Turn-Over. TO) 이 27. 6 등급보다 밝은 지점 (그래프의 왼쪽) 에 있어야 합니다.
이런 논리로 추정하면 구상성단 광도함수로 거리를 잴 수 있는 한계거리를 계산할 수 있습니다. 내용을 아래에 정리했습니다. <그림 12 구상성단 광도함수로 거리를 잴 수 있는 한계거리. 사진은 NGC 4881 (타원은하. 구상성단이 아님). NGC 4881 거리출처 : 그림 9 와 동일> 100 Mpc 이란 거리는 Hubble 망원경이 1995 년에 측정한 자료를 기준한 것입니다. 근래에는 다양한 우주망원경이 더 먼 은하에서 훨씬 더 어두운 구상성단의
안시등급을 측정했을 수도 있습니다. 새로운
자료가 구해지면 업데이트 하겠습니다. (6) Face-On, Edge-On 나선은하의
구상성단 위 단락들에서 인용한 먼 거리
은하는 NGC 4494 (타원), NGC 4565 (나선, Edge-On), NGC 4881 (타원) 으로, 타원은하 두 개와 Edge-On 나선은하 한 개 입니다. 이런 은하들이 인용된 이유가 우연은 아니며, 이들 은하에서 구상성단이 쉽게 관측되기 때문입니다. 예를 들면, 건물이 밀집되어 있고 형형색색 네온사인 간판이 빛나는 번화가에서 어떤 특정한 간판을 찾아내기는 어렵습니다. 다른 네온간판에서 나오는 다른 색깔 빛이
해당간판 색깔에도 영향을 줄 수도 있고, 건물창문에서 나오는 빛도 방해가 되어 그 간판의 본래밝기를
측정하기는 쉽지 않을 겁니다. 심각한
자동차 매연도 네온간판의 광도측정에 영향을 줄 수 있습니다. 그러나 조용한 시골동네 어두운 거리의 네온간판은 이런 요인들의 방해 없이
광도측정이 한결 쉬울 것입니다. 이런
예는 나선은하에서 구상상단을 관측할 때 똑같이 적용됩니다. 지구 시선방향에서 전면 (全面)
이 보이는 나선은하 (Spiral Galaxy) 를 Face-On (페이스 온) 나선은하라 합니다. 이 경우는 은하면이 시선방향과 90° 가 됩니다.
위 단락에서 은하 테두리만 보이는 나선은하를 Edge-On (엣지 온) 나선은하로 부른다고 말씀 드렸습니다. 이 경우는 은하면과 시선방향
사이의 각도가 0° 입니다. 그런데 모든 은하에서 대부분
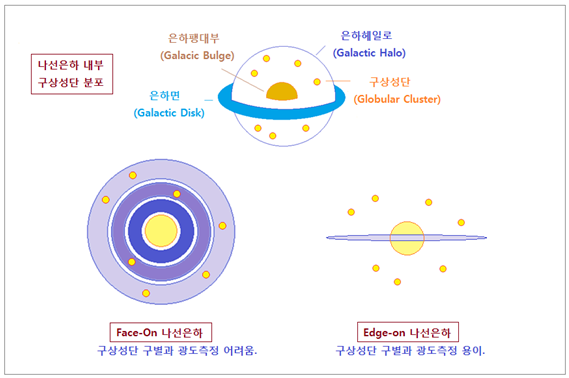
구상성단들은 은하 Halo (헤일로) 에 자리잡고 있습니다 (한담객설 2015. 8. 30 일자 참조). 따라서 Face-On 나선은하에서 구상성단을 찾아 안시밝기를 측정하는 것은 번화가에서 특정간판을 찾는 것과 비슷합니다. 그러나
Edge-On 나선은하의 뒷 배경은 캄캄한 우주이므로 훨씬 더 쉽게 찾아지고 정확하게 측정됩니다. 이런 내용을 아래에 정리했습니다. <그림 13 Face-On 나선은하와 Edge-On 나선은하에서 구상성단 구별과 광도측정 용이성 비교> (7) 타원은하의
구상성단 타원은하 (Elliptical Galaxy) 안에는 같은 지름의 나선은하, 불규칙은하에
비해 더욱 많은 구상성단이 있습니다. 또한
나선은하에선 나선팔은 밝고, 다른 부분은 어두운데 비해, 타원은하의
표면밝기는 전체적으로 거의 비슷한 수준이며, 은하내부 천체에서 방출되는 여러 종류 빛이나 전파 등 차폐물로
인한 소광 (消光. Extinction by Intervening Material) 도 적습니다. 이런 이유로 타원은하 내부 구상성단은 광도함수를 측정하기 가장 적합한
은하가 됩니다. 타원은하에서도 Halo 가 존재하지만, 구형인 은하모양 때문에 그 경계선이 나선은하처럼
확실히 구별되진 않습니다. 그렇더라도
구상성단이 주로 Halo 에 분포한다든지, 또는 구상성단
소속 별들이 타원은하 중심부 별들보다 나이가 많고, 금속함량
(Metallicity. 수소와 헬륨을 제외한 다른 원소비율) 이 적다는 사실은 나선은하
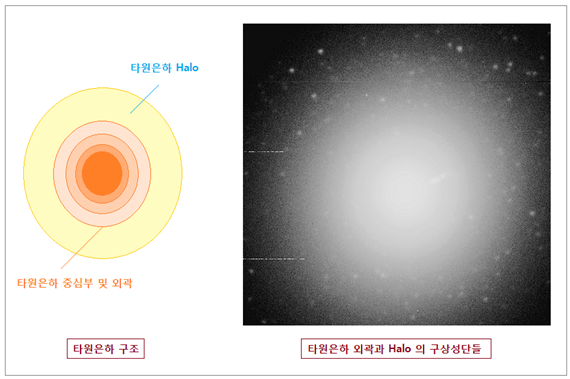
경우와 동일합니다. 아래 그림은
타원은하 구조와 특정 타원은하에 보이는 구상성단들입니다. <그림 14 타원은하에서의 구상성단 관측. 타원은하 사진출처 : spiff.rit.edu/classes. 출처에
해당 타원은하 명칭 없음> (8) 아이디어의 Shapley, 액션의 Baum 구상성단
광도함수에 대한 토대를 제공한 사람은 잘아시는 Harlow Shapley (1885~1972. 미국) 입니다.
그는 1953 년에 우리은하, M31 및 LMC 내부 구상성단들의 평균 본래광도가 일치하는 것을 발견하고, 이것이
거리측정 기준인 Standard Candle 이 될 수 있다고 제안했습니다. 당시에 구상성단 연구에 관한 한, 그를 능가할 학자는 없었던 듯 보입니다. 그러나 그가 직접 이것을 이용해서 다른 은하들까지 거리를 측정하진 않았습니다. 이런 Shapley 의 아이디어를 실행에 옮긴 사람은 William Alvin
Baum (바움. 1924~2012. 미국) 입니다. Baum 은 천문학자이지만, 고속 Spectrograph 등 몇가지 천문관측도구를 발명하거나
개선하는데도 능력을 발휘했습니다. <그림 15 William Alvin (Bill) Baum (1924~2012) 사진 및 그의
업적일부. 사진은 45 세 모습. 출처 : 미국천문학회 웹사이트.
American Astronomical Society. aas.org> 위 그림은
미국천문학회 웹사이트에 실린 그의 업적 일부입니다.
Shapley 가 아이디어를 제안한 직후로 추정되는 같은 1953 년에, Allan Sandage (1926~2010. 미국) 및 Halton Arp (1927~2013. 미국) 와 공동작업 하면서
구상성단으로 거리를 측정한 사실이 소개되어 있습니다. 또 다른 자료에선 구상성단 광도함수가
Baum 의 업적이라고만 명시된 것을 보면, Baum 이 독자적으로 진행한 연구로 추정됩니다. 이 분
업적을 살펴보니 다양한 기계를 발명하거나 개선했고, 지금은 저명한 학자 반열에 드는 여러 학자들과 같이
작업했었습니다. 그럼에도 거의
잊혀진 이름이 된 이유는 결정적 한 방이 없었기 때문이라고도 할 수 있습니다. 하지만 구상성단 광도함수에서 비롯된 “광도함수” 용어는 다른 종류 천체에도 적용되고 있고, 천문학에선 일반명사처럼
사용됩니다. 구상성단
광도함수 방법을 Baum 이 처음 개발한 것은 아닙니다. 그러나 Hubble 이 M31 은하거리를 쟀던 Cepheid 변광성 방법도 Hubble 이 개발한 것은 아닙니다. Baum 이란 이름이 현재 거의 잊혀진 까닭이 결정적 한 방이 없어서라기
보다는, 지난호에서 말씀드린 Oepik 경우처럼 자기홍보
부족에 기인하지 않을까 생각합니다. 겸손은
지역과 시대를 불문하고 미덕으로 여겨집니다. 그러나 업무에서의 지나친 겸손은 스스로 능력발휘 기회를 없애버리는 것과
같을 겁니다. Oepik 과 Baum 이 요즘같은 매스미디어 시대에 살았더라면, 상황이 어찌되었을지
생각해보게 됩니다. 다음호에서도
계속 우주거리에 대해 말씀드리겠습니다. <그림 16 배경그림출처 : 한담객설 2015. 8.16일자 그림 26 과 동일. 편집. 추가>
II. 담천잡담 다른 문화 다른 별자리
(5) – 북극권 원주민의 Orion Belt (1) 북극권이란
? 이번 담천잡담에선 북극권 원주민이 생각한 Orion Belt 세 별에 대해 알아 보겠습니다. 우선 북극권은 정확히 무슨 뜻인지부터 살펴봅니다. 보통 북극권 (Arctic Circle) 에선 태양이 지평선을 따라 움직여서 해가 지지 않는 기간이 일년에 6 개월이나 되고, 반대로 해가 뜨지 않아 밤이 지속되는 기간이 일년에 6 개월 정도 된다고 알려져 있습니다. 따라서 밤이 6 개월이나 계속되므로
그 지역에선 별자리 관련 전설이 엄청 많을 듯 생각되고, 수 많은 별들에 이름이 붙어 있을 것으로 여겨집니다. 그러나 이런 얘기는 잘못 알려진 상식이며, 실제로 밤이 지속되는 기간은 “지역에 따라” 이보다 훨씬 짧습니다. 또한 눈보라 등 날씨의 영향으로 청명한 밤하늘을 볼 수 있는 기간은 더욱
짧아지게 됩니다. 그러면 북극권에서 해가 뜨지 않고 밤이
지속되는 기간은 과연 얼마나 될까요 ? 상식적으로
생각해도 밤이 지속되는 기간이 북극권 모든 지역에서 같지는 않을 것입니다. 지역에 따라 밤의 지속기간이 얼마나 되는지 알아보려면 북극권의 정의부터
살펴보아야 할 겁니다. 남극권 (Antarctic Circle) 은 북극권 조건과 반대이므로, 여기선
북극권을 중심으로 말씀 드리겠습니다. 북극권이란, “태양이 지평선 위 또는 아래에 하루 (24 시간) 이상 머무는 지역의 남쪽한계선” 을 말합니다. 남극권인 경우는 북쪽한계선을 뜻합니다. 태양이 지평선 위 또는 아래에 하루 이상
머문다는 뜻은 어떤 날에는 하루 종일 낮이 계속되거나 (白夜. White Night) 또는 밤이 계속되며 (極夜. Polar Night),
그 한계선 북쪽으로 갈수록 하루 종일 낮이 계속되는 날 또는
밤이 계속되는 날이 점점 늘어난다는 의미입니다.
(2) 헷갈리는 북극권의 낮과 밤 이런 현상이 생기는 이유는 지구자전축이
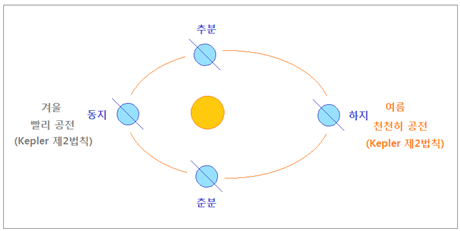
황도면 수직방향에 대해 기울어져 있고, 또한 지구가 태양을 공전하기 때문입니다. 아래 그림 보시지요. <그림 17 지구자전축 기울기 및 지구의
태양 공전> 지구자전축은 일정각도로 기운 상태로 태양을
공전하며, 이에 따라 계절 변화가 나타납니다. 공전궤도는 타원이고, 여름에는
태양으로부터 거리가 멀고 겨울에는 가까워집니다.
그런데 Kepler 제 2 법칙에
따르면 행성은 공전하면서 일정시간 동안 같은 면적을 쓸고 지나갑니다. 따라서 여름에는 공전속도가 겨울보다
느리고, 겨울에는 공전속도가 여름보다 빨라짐을 예상할 수 있습니다. 그러면 지구자전에 따른 낮과 밤 길이는
위도에 따라 어떻게 변하는지 알아 보겠습니다.
<그림 18 지구자전에 따른 위도별 낮과
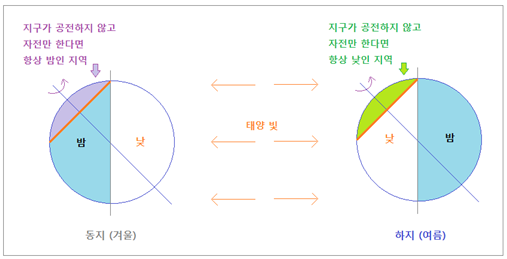
밤 길이 변화> 왼쪽 그림은 겨울의 “동지” 때의 지구자전 모습입니다. 만일 지구가 “공전궤도상에서
동지 위치에 항상 머물며 공전하지 않고 자전만 한다면”, 보라색 칠한 부분에선 지구가 자전해도 항상
밤만 계속됨을 알 수 있습니다. 동지
때의 황색선 지점의 위도에선, 지구대기 굴절현상이 없다면, 하루
동안 태양의 중심이 지평선을 잠시 스쳐 지나갈 뿐이고, 나머지 시간은 모두 밤일 될 겁니다. 그 지점의 바로 북쪽인 보라색 부분 위도부터는 지구가 공전하지 않고 자전만 한다면 영원히 태양을 볼 수 없습니다. 오른쪽 그림은 여름 “하지” 때 모습입니다. 만일 지구가 “공전궤도상에서
하지 위치에 항상 머물며 공전하지 않고 자전만 한다면”, 초록색 칠한 부분에선 항상 낮만 계속됩니다. 하지 때의 황색선 지점의 위도에선, 역시 지구대기 굴절현상이 없다는 가정 아래, 하루 동안 태양원반
중심만 고도가 낮아져 잠시 지평선을 스쳐 지나가고 나머지 시간은 모두 낮일 겁니다. 그 지점의 바로
북쪽위도부터는 지구가 공전하지 않고 자전만 한다면 태양은 영원히 지평선 위에서 움직일 겁니다. 그런데 지평선을 스쳐 지나가는 것은 태양원반의
중심이며, 태양의 윗부분 (동지) 또는 아래부분 (하지) 이
아닙니다. 따라서 동지에 태양
중심이 남쪽 지평선을 지나가는 때는 박명처럼 어느 정도 환해집니다. 하지에 태양중심이 북쪽 지평선을 지날 때는 완전히 낮이 아니라 박명처럼
어슴푸레한 상태가 됩니다. 이런
상항은 아래 단락에서 그림과 같이 다시 말씀 드리겠습니다. 또한 지구대기로 인한 굴절현상 때문에
태양 윗부분이 실제로는 지평선 조금 아래에 있어도, 지평선 위로 약간 올라온 모습으로 보입니다. 이 현상을 감안하면 <그림 18> 의 황색선은 남쪽으로 90~100 km 더 가서 그려진다고 합니다. 여기선 이 현상을 감안하지 않고 말씀 드리겠습니다. 지구대기로 인한 굴절현상에 대해선 아래
칼럼들을 참조하시기 바랍니다. • Astro News Serial No 4. 2nd
issue of Mar. 2012 (지구대기로 인한 굴절과
춘분의 낮 길이) • Astro News Serial No 9. 1st
issue of July. 2012 (지구대기로 인한 Mirage. 신기루 현상). 지구는 자전하면서 태양을 공전합니다. <그림 17> 에서 보시듯이 지구가 공전궤도를 따라 움직이면서 자전축이 태양을 향하는 방향이 시시각각 변동하며, 이에 따라 하루 중에서 낮 시간과 밤 시간에 차이가 나게 됩니다. 봄에서 여름기간에는 하루 중에 낮 시간이 더 길고, 가을에서 겨울에는 하루 중에 밤 시간이 더 길어집니다. 황색선 위도지역에선 일년 중에 밤 또는
낮만 계속되는 기간이 동지 또는 하지의 하루에 불과하지만, 위도가 점점 북쪽으로 갈수록 그 일자는 늘어나게
됩니다. 보라색 또는 초록색 지역
중간인 N 78° 부근에선 겨울 동지 전후로 밤만 계속되는
기간이 대략 90 일이고, 여름 하지 전후로 낮만 계속되는
기간은 92 일 정도입니다. 그 남쪽인 N 70 ° 부근에선
동지 전후 밤 기간이 45 일, 하지 전후 낮 기간이 47일 정도라고 합니다. 위도가
N 90° 인
북극에선 여름에 낮만 계속되는 기간이 186 일 (약 6. 2 개월) 이고 겨울에 밤만 계속되는 기간이 179 일 (5. 9 개월) 정도
입니다. 밤과 낮 기간이 정확히
일년의 반인 182~183 일이 아니라 낮 기간이 더 긴 이유는
Kepler 제 2 법칙 때문입니다. <그림 17> 보시면
여름기간에 지구는 겨울기간보다 공전궤도를 더 천천히 공전합니다. 하지만 자전속도는 계절에 관계없이 항상 동일하므로 여름기간이 약 7 일 더 길게 되고, 이에 따라 낮만 계속 되는 기간이 더 길게
됩니다. (3) 원인은 지구자전축 기울기 그림에서 보시듯이 황색선이 바로 북극권의
남쪽한계선이 되며, 그 지점의 위도는 지구가 완전한 구체라고 가정하면 (90° – 해당시점의
지구자전축 기울기) 가 됩니다. 그런데 지구자전축 기울기는 지금 이 순간에도 계속 변동되고 있습니다. 여기선 다가오는 새해를 기다리며
2016 년 1월 1일 현재 지구자전축 기울기를
찾아 보겠습니다. <그림 19 2016년 1월 1일 지구자전축기울기 (황도경사각) 출력자료. UT
0:00 기준. 출처 : PHP Science Labs. neoprogrammics.com>
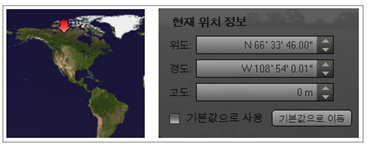
위 인용 프로그램으론 2016 년 1월 1일 지구자전축 기울기가
23. 4372 1087 69° (23° 26’ 13.
959”) 로 출력됩니다. 이
수치에 따른 북극권은 아래와 같이 정리됩니다. •
2016 년 1월 1일 현재 북극권의 남쪽한계선 (북극권 경계선) : N 66.
5627 8911 31°
(약 N 66. 56°) 또는 N 66° 33’
46. 041” (약 N
66° 33’ 46“ ) 참고로
지구자전축 기울기는 약 40,000 년 주기로
약 2° 폭으로 변동하며, 근래에는 매년 약
0. 00013° (0. 468 “ ) 씩 줄어들고 있습니다. 이는 자전축이 똑바로 서 간다는 뜻입니다. 이런 상태는 AD 8225 년경까지 계속되다가 기울기가 다시 증가하기 (눕기) 시작합니다.
미세한 장동 (章動 Nutation) 효과를 배제할 경우의 변동내역은 아래와 같습니다. 장동은 자전축 기울기가 9.
3년 동안 10~25초 사이에서 감소 또는 증가하며 한 주기가 18. 6 년인 현상입니다. 지구자전축
기울기 변동추이에 대해선 한담객설 2014 년 12월 10일자를 참조하시기 바랍니다. • 변동폭 : 22° 2’ 33” ~ 24° 30’ 16” (또는 22° 13’ 44” ~ 24° 20’ 50”) • 변동주기 : 41,040 년 (약
40,000 년 주기로 약 2° 폭으로 변동)
하여간 북극권 남쪽한계선
위도가 (90° – 해당시점의 지구자전축 기울기) 이며, 현재 지구자전축 기울기가 매년 약 0. 00013° (0. 468 “) 씩 줄어들고 있으므로 북극권
남쪽한계선 위도는 매년 그만큼씩 “북쪽으로 올라가고” 있습니다. 0. 00013° (0. 468 “) 는 지구위도상 거리로 약 14. 5 m 입니다. 따라서 북극권 경계선은 지금 위치에서 AD 8225 년까지 약 90 km 북쪽으로 올라갔다가 다시 2 만년 동안 남쪽으로 내려오고, 그 후 2 만년 후에는 다시 올라감을 반복할 겁니다 <참고> • 0.468” 의 지구 위도상 길이 : 40,007. 860 km x 0.
00013° / 360° = 0. 0144472828 km = 14.
447 m = 약 14. 5 m. • AD 8225 년까지 북극권경계선 이동거리 : (8225년 – 2015 년) x
14. 5 m = 90. 045 km. 아래 그림의 점선을 2016 년 1월 1일 현재 북극권 남쪽한계인
N 66. 5627 8911 31° (66° 33’
46. 041” ) 로 생각하시면 될 듯합니다 (약 N
66. 56°. N 66° 33’). 점선내부가 북극권입니다. <그림 20 왼쪽 북극권 범위. 출처
: smartmeetings.com> (4) 북극권 경계선에 서서
1. 하지의 태양궤적 이제는
2016 년 하지인 6월 21일에 위 그림의
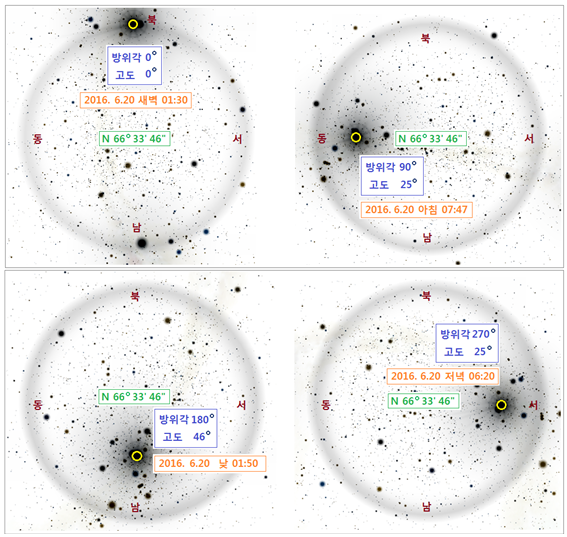
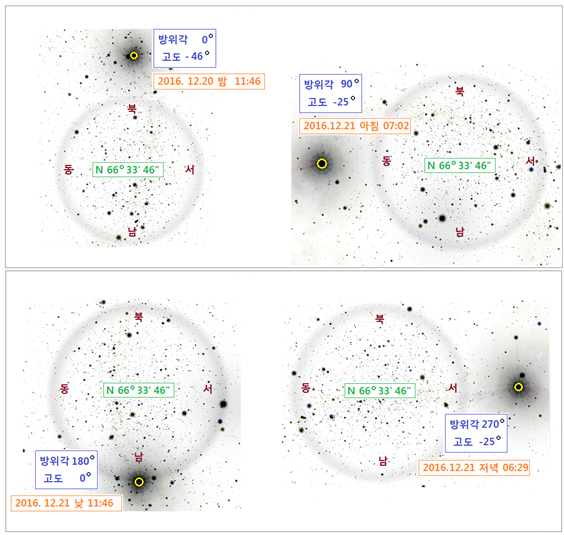
점선 표시된 북극권 남쪽한계선 위도에서 태양은 하루 동안 어떤 궤적을 그리며 이동하는지 찾아보겠습니다. 이 지점은 <그림 18> 에서 황색선 위치 및 <그림 20> 에서 점선위치가 됩니다. <그림 21/22/23 북극권 남쪽한계선
위도 (N 66° 33’ 46”) 에서 현지시간 2016 년 6월 20일 (하지) 의 태양 일주궤적.
출처 : Stellarium 화면. 편집. 추가>
태양일주 관측위치는 캐나다 북부 북극권
남쪽한계선인 N 66° 33’ 46” 입니다. 한국시간으로 2016 년 하지는 6월 21일 아침 7시 34분입니다.
위에 표시 드린 캐나다 북부 관측위치의 현지시간으론 섬머타임 (Daylight
Saving) 이 적용되어 6월 20일 오후 4시 34분이 됩니다. 이에 따라 현지의 관측일자 및 시간을
6월 20일 새벽부터 시작했습니다. 위 네 가지 그림을 <그림
18> 의 하지 경우와 비교해 보시기 바랍니다. 6월 20일 새벽 01시 30분에 태양은 정북 방향에 있으며, 이 때는 방위각 0° 고도 0° 입니다. 그런데 태양고도가 0° 라는 말은
태양의 중심이 지평선에 걸쳐 있다는 뜻이므로, 태양 원반의 윗부분 반은 지평선 위에 있게 됩니다. 따라서 지상은 아침의 박명처럼 어느 정도
밝을 것임이 예상됩니다. 이후 태양이 동쪽, 남쪽, 서쪽으로 이동하면서 태양은 항상 지평선 위에 있으므로 하루 종일 낮이 계속됩니다. 하지는 북반구에서 태양의 고도가 일년 중에 가장 높아지는 날입니다. 지구가 공전하면서 하지 이후에는 태양
고도가 점차 낮아지므로 태양은 북쪽에서 아주 가까운 북동쪽에서 뜨기 시작해서 북쪽에서 아주 가까운 북서쪽으로 지기 시작합니다. 따라서 이 위도에선 하지 하루만 하루
종일 낮이 계속 됩니다. 여기서 잠시 위 그림의 태양 남중고도가 맞는지 계산해보고 지나기겠습니다. 남중고도 수식에 대한 사항은 지난 한담객설 2014년 12월 10일자를
참조해 주십시오. • 남중고도 (h) 계산식 :
Φ : 관측지점
위도. δ : 관측일자의 태양적위
(Φ – δ) > 0 이면 : h = 90°
– (Φ – δ). (Φ – δ) < 0 이면 : h
= 90° – (δ – Φ). • 따라서 h = 90°
– (66. 5627° – 23. 4372°)
= 46. 8745° 위 그림에서 태양이 남중한 상태의 고도를
46° 로 표시 드렸습니다. 이 위치에서의 정확한 고도 및 지구자전축
기울기 (황도경사각) 는 아래와 같습니다. 위 계산결과에 거의 근접한 수치임을 알
수 있습니다. 계산결과와 Stellarium 수치차이는 위 그림의 시간이 정확한 하지시점은 아니고, 지구자전축
기울기 계산프로그램이 PHP Science Labs 와 Stellarium 에 다소 차이가 있어 생긴 것입니다. <그림 24 북극권 남쪽한계선 위도 (N 66° 33’ 46”) 에서 현지시간 2016 년 6월 20일 (하지) 의 태양
남중고도. 출처 : Stellarium 화면. 편집.
추가> 2. 동지의 태양궤적 그러면 동지 때는 태양궤적이 어떻게 되는지 알아보겠습니다. <그림 25/26 북극권 남쪽한계선 위도 (N 66° 33’ 46”) 에서 현지시간 2016 년 12월 20~21일 (동지) 의 태양 일주궤적.
출처 : Stellarium 화면. 편집. 추가>
한국시간 동지는 2016 년 12월 21일 저녁 7시 44분 입니다.
<그림 18> 황색선 위 관측위치에서의 동지시각은 섬머타임 (Daylight Saving) 이 없을 때이므로 12월 20일 새벽 3시 44분이
됩니다. 이 날짜를 전후한 태양의
궤적은 위 그림과 같습니다. 동지는 북반구에서 태양의 고도가 가장 낮은 날이므로, 이 위도에선 하지와는 반대로 하루 동안 남쪽에서 태양원반 중심만 잠시 걸칠 뿐, 태양이 지평선 위로 올라오지 않습니다. 따라서 동지 하루 동안은 종일 밤이 계속됩니다. 다만 태양원반 중심이 지평선에 걸칠 때는
위에서 말씀 드린 것처럼 박명 때문에 어느 정도 밝을 것입니다. 지구공전에 따라 동지 이후에는 해가 뜨고 지는 것이 다시 시작됩니다. 위 그림에서 태양 남중고도는 아래와 같이 계산됩니다. • h = 90°
– {66. 5627° – (
– 23. 4372°)}
= 0° 북극권 경계선 위도에서 북쪽으로 갈수록 하지 전후로 해서 낮이 계속되는
기간과 동지 전후로 밤이 계속되는 기간이 점점 늘어납니다. 원칙적으로 본다면 북극점에선 낮이
185~186 일 계속되고 밤이 179~180 일이나 지속되어야 합니다. 과연 그럴까요 ? 북극점에서 태양은 날짜별로 고도만 바뀔 뿐, 일년 내내 지평선에 평행하게 움직입니다. 춘분에는 태양중심이 하루 종일 지평선을 따라 움직이고 (고도 0 °), 매일 고도가 높아져 하지에 최고 고도 (그 때의 지구자전축 기울기) 에 이릅니다. 하지를 지나면 고도가 점차 낮아져 추분에
춘분과 동일하게 하루 종일 지평선을 따라 움직이고 (고도 0 °), 이후엔
지평선 아래로 들어가 동지에 최저 고도 (그 때의 지구자전축 기울기의 음수) 에 이릅니다. 동지 이후에는 다시 고도가 높아집니다. 한편 춘분 얼마 전 및 추분 얼마 후에, 태양의 윗부분이 하루 종일 동서남북 모든 방향의 지평선 바로 아래를 수평 이동할 때를 생각해 보겠습니다. 이 때에는 실제태양은 지평선 바로 아래에
있지만, 지구대기 굴절현상 때문에 태양 윗부분이 지평선 위로 보여서 하루 종일 어느 정도 환해지는 기간은
각각 약 3 주가 되어 모두 6 주가 됩니다. 따라서 한달 반 (45 일) 은 밤에도 어느 정도 환하므로 하루 종일 밤이 계속된다고는
말할 수 없습니다. 이런 날들을 제외하면 북극점에서 하루 종일 캄캄한 밤이 지속되는
기간은 4 개월 반 (135 일) 정도 됩니다.
그러나 이 기간 중에서도 여러 날들에서 눈보라, 오로라 등이 밤하늘 관측에
방해가 되며, 지상의 눈 때문에 달 빛 반사도 심하다고 합니다. 이 같은 기상조건까지 모두 감안한 일년 중 북극점에서의 청명한 밤 기간은
약 2 개월 반 (75 일)
에 불과합니다. 하여간
북극권에서 살려면, 일년 중 변동폭이 큰 낮과 밤 시간에 적응하는 특별한 생체리듬이 필요할 것 같습니다. (5) 단순명쾌한
Inuit 전설 보통
Eskimo (에스키모) 로 알려진 북극권 원주민을 언어에 따라 크게 분류하면 러시아 북동부와 Alaska 북서부에 사는 Yupik (유픽) 과 캐나다 북부에 사는 Inuit (이누이트) 로 구분됩니다.
Eskimo 단어의 어원은 불분명하다고 하며, 그들 언어로 “날고기를 먹는 사람들” 로 추정된다고 합니다. 그러나
Eskimo 단어는 당사자인 원주민이나 국가에서 권장하지 않는 용어이며, First Nations 또는
부족이름인 Yupik 과 Inuit 가 선호됩니다. Yupik 은 원주민 언어로 “Real People (진짜 사람들)” 뜻이고 Inuit 는 “Human (인간)”
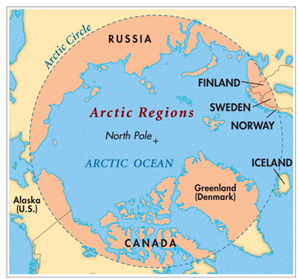
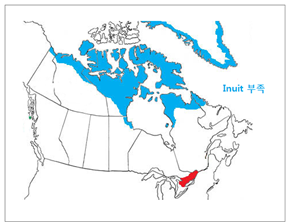
입니다. 아래 그림은 캐나다 북부 및 덴마크 소속
자치령 Greenland 의 Inuit 거주지입니다. 이들 지역 대부분이 <그림 20> 에 표시 드린 북극권 경계선 내부에 있습니다. <그림 27 캐나다 및 Greenland 의 Inuit 부족 거주지. 출처 :
Simon Fraser University. sfu.ca> Orion
Belt 세 별에 대한
Inuit 전설은 다음과 같습니다. 어느 날, Inuit 남자 네 명이 북극곰 사냥을 나갔습니다. 하루 종일 쫓기던 곰은 지평선 끝에 도달하자 더 이상 갈 곳이 없어 밤하늘로 훌쩍 뛰어 올라갔습니다. 사냥꾼들도 지평선과 밤하늘이 맞닿은 곳에서 하늘로 들어가 계속 곰을 쫓아갔습니다. 네 명 사냥꾼들이 하늘에서 곰을 쫓아가던 중에, 그 중 한 명이 한 쪽 장갑을 놓쳐 땅으로 떨어지고 말았습니다.
장갑을 놓친 사냥꾼은 손이 시려워 더 이상 곰을 쫓을 수 없었고 할 수 없이 땅으로 내려왔습니다. 나머지 세 명은 지금도 하늘에서 곰을 쫓아가고 있으며 이들이 Orion Belt 세 별이라고 합니다. 이 이야기는 땅으로 내려온 후, 다시 하늘로 올라가지 않았던 사냥꾼이 전해준 얘기라고 합니다. 이 전설에서 세 명 사냥꾼 얘기는 그럴듯합니다. 그런데 그들이 쫓아가고 있는 북극곰은
어느 별자리인지 얘기가 없어 궁금합니다. 일단 Orion 자리의 사자가죽 방패부분으로 생각하고 Inuit 별자리
그림을 그려보았습니다. <그림 28 Inuit 전설의 Orion Belt 와 북극곰. 원주민과 곰디자인 :
cliparkiscrum.com. 편집> Inuit 전설은 그리이스 버전 Orion 신화에서 Orion 이 사냥꾼인 것과 신기하게 닮았습니다. 그러나 전설이 그리이스 신화처럼 복잡하지 않고 단순하며, 외도 질투 모략 살해교사 등 그리이스 신화처럼 지저분한 내용 없이 명쾌합니다. 단순한 자연환경 속에서 오로지 생존만을 위해 투쟁해온 그들 생활을 반영한
듯 보입니다. III. 월하산책
잃어버린 별자리를 찾아서 (22) – 작은삼각형 Triangulum Minus (1) 작은삼각형 – 나
만든 사람 나와 봐 ! 이번 월하산책에선 작은삼각형 자리를 찾아보겠습니다. 현존하는 별자리로 북반구에 이미 삼각형 (Triangulum) 이 있고, 남반구에도 남쪽삼각형 (Triangulum Australe) 이 있어서 작은삼각형까지 살펴보려니 좀 헷갈립니다. 차제에 이들 세가지 모두 알아보려 합니다. 작은삼각형 자리 (Triangulum Minus) 는 1687 년에 Johannes Hevelius (1611~1687. 폴란드) 가
만든 것입니다. 그의 사후에 출판된 1690 년 성도에 처음 실렸습니다. 우선 Hevelius 의 성도부터
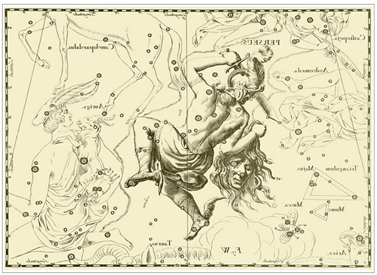
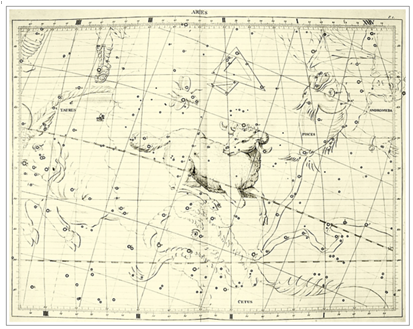
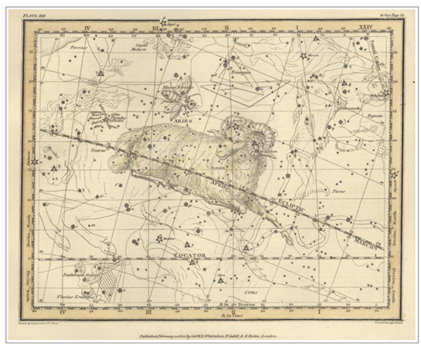
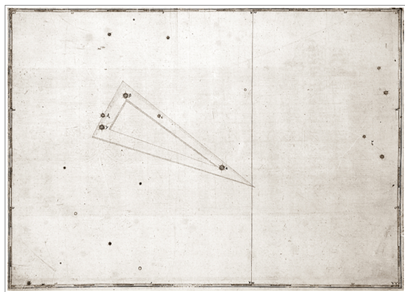
보시지요. <그림 29/30 Hevelius –
Uranographia (1690) 및 부분확대. 출처 : Tartu Observatooriumi Virtuaalne Muuseum> 1690
Hevelius 성도는 일반성도의 좌우도립 이미지 입니다. 위 그림은 Hevelius 성도를 일반성도 방향과 맞도록 다시 좌우도립 시킨 것입니다.
Hevelius 는 기존의 삼각형자리를 큰삼각형 (Triangulum Majus) 으로
이름을 바꾸고, 작은삼각형을 끼워 넣었습니다. 아래에선 작은삼각형이 실린
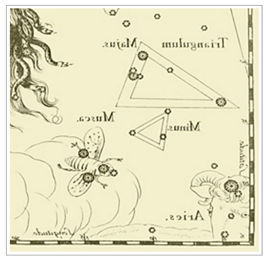
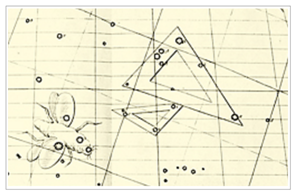
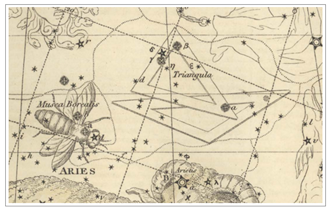
Hevelius 이후 성도 몇 개를 보여 드립니다. 모든 성도에서 양 머리 북쪽에 삼각형과 작은삼각형이 있습니다. <그림 31/32 Flamsteed – Atlas Coelestis (1753) 및 부분확대. 출처 : 그림 29 와 동일> 1753 년 Flamsteed 성도 확대부분 보시면
별자리 이름표시는 없습니다. 그러나
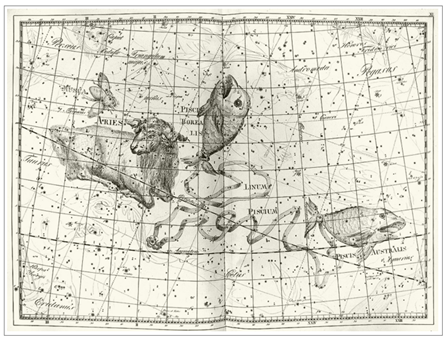
작은삼각형을 이루는 세 별이 분명히 그려져 있으므로 작은삼각형 자리를 표현했다고 보여집니다. . <그림 33/34 Bode – Uranographia
(1801) 및 부분확대. 출처 : 그림 29 와 동일> 1801 년 Bode 성도에선 삼각형이 큰삼각형 (Triangulum Majus) 으로 적혀있고, 작은삼각형은 Triangulum 이 생략되어 단순히 Minus 로 표기되어 있습니다. 그런데 아래 성도에서부턴 작은삼각형을
표시한 것인지 아닌지 헷갈리기 시작합니다.
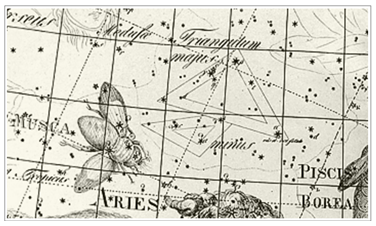
<그림 35/36 Jamieson -
Celestial Atlas (1822) 및 부분확대. 출처 :
ianridpath.com> 1822 년 Jamieson 성도는 1801 년 Bode 성도를 기초로 만들어진 것입니다. 그러나 삼각형과 작은삼각형 자리에 대해선 Bode 성도와 조금 다릅니다. Bode 성도는 Triangulum
Majus (큰삼각형) 와 Minus (작은) 로 분명히 구분되어 되어 있었으나, 여기선 삼각형 두 개를 그려
넣고, Triangula 로 적어 놓았습니다. Triangula 는 라틴어로
Triangulum 의 복수형 (삼각형들) 입니다. 또한 작은삼각형을 이루던 별 세 개는
표시되어 있지만, 다른 별들도 같이 표기되었기 때문에 작은삼각형이 별도로 구분되진 않습니다. Jamieson 생각에 작은삼각형을 이루던
세 별은 어두운 별들이라 두 개 삼각형을 삼각형들 (Triangula) 이란 단일 별자리로 통합한 것
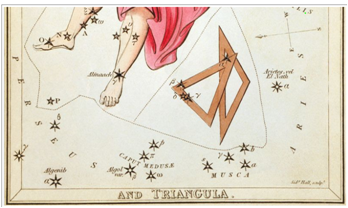
같습니다. <그림 37 Jehoshaphat Aspin –
Urania’s Mirror 일부 (1825). 영국. 수작업
채색. 출처 : commeons.wikimedia.org>
1825 년 채색성도에서도 작은삼각형은 Jamieson 성도처럼
삼각형에 통합되어 Triangular 로 그려졌습니다. 성도 아래쪽 테두리에 별자리 이름이 보입니다. 이것은 카드형 (Card) 성도로서, 별을 찾기 위한 성도라고는 볼 수 없고 대강의
별자리를 묘사한 것이라 별 위치에 큰 의미는 없을 듯합니다. 참고로 왼쪽에 보이는 사람 발은
Andromeda 의 발 입니다 그러면 밤하늘에서 작은삼각형의 정확한
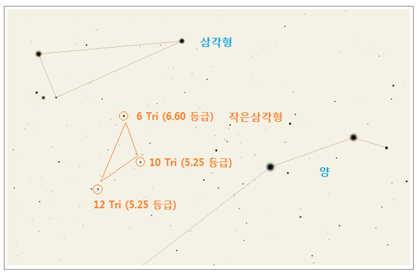
위치는 어디일까요 ? 작은삼각형을
이루는 세 별의 안시등급을 찾아보니 5. 25~6. 60 등급이었습니다. 17 세기엔 이렇게 어두운 별들로도 거리낌
없이 별자리를 만들 수 있었나 봅니다. <그림 38 작은삼각형 자리 위치. 출처 : Stellarium 화면.
편집. 추가> 이 별자리는 1687 년에 태어났으나 1822 년 Jamieson 성도에서부터 본명을 잃고 삼각형에 흡수통합되는 치욕을 맛보았습니다. 드디어
1928~1930 년에 이르러 IAU 에 의해 공식퇴출 되었으니 243 년을 산 셈입니다. 짧고 굵은 삶이 아니라, 짧고
희미한 성생 (星生) 입니다. 아래 단락에서 보시겠지만, 삼각형자리는 크기는 작지만 역사와 전통이 있는 별자리 입니다. 이런 별자리 옆에, 재미로
만들었는지 아니면 취중작품인지는 모르겠으나 Hevelius 가 쓸데없이 비슷한 별자리를 하나 더 끼워
넣어 작은삼각형만 허무하게 만들었습니다. 작은삼각형이
살아있다면 금년에 328 살이 됩니다. 이제는 결코 적은 나이가 아니므로 땅 속에서라도 이렇게 외치고 싶을지
모릅니다. “나 만든 사람 나와
봐 !” (2) 삼각형 – 내
나이는 2,300 살 삼각형자리 (Triangulum) 는 Sumer 별자리는 물론, 이를 계승한 Egypt 의
Dendera Zodiac 에도 나타나지 않습니다. 이 별자리에 대한 최초의 기록은 BC
3 세기에 그리이스에 살았던 Aratus (BC 315/310 ~ BC 240) 가 남긴
것입니다. Aratus 는 삼각형자리를
이등변삼각형 (Isosceles Triangle) 모양이라고 표현하고,
Deltoton (델토톤) 으로 불렀습니다. Deltoton 은 그리이스어의 영어표기이며, 요즘 영어로 Delta 입니다. 그리이스어 Delta 의 대문자는
Δ 이며, 모양이 이등변삼각형입니다. 위의 현대성도 보시면 삼각형자리가 완전하진 않지만 이등변삼각형임을 알
수 있습니다. 지구둘레 측정으로 유명한 그리이스계 Egypt 사람 Eratosthenes (에라토스테네스 BC 276~BC195/194) 는 삼각형자리가 Egypt Nile 강 (나일강) 의 삼각주 (Delta)
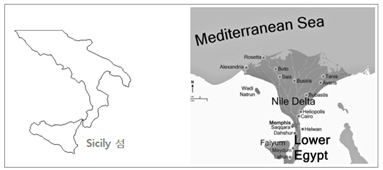
모양을 딴 별자리란 기록을 남겼다고 합니다. 로마시대 Hyginus (히기누스 BC 64~AD 17) 는 삼각형자리가 Sicily (시실리) 섬으로 불린다는 기록을 남겼습니다. Sicily 섬의 로마시대 이름은
Trinacria 이며, 삼각형이란 뜻입니다. <그림 39 Sicily 섬과 Nile 강 삼각주> 이런 기록들로 본다면, 삼각형자리는 그리이스에서 만들어진 별자리임이 분명해 보입니다. 아마 처음에는 Aratus 기록에
보이듯이 단순히 델타글자 (Δ) 를 딴 별자리로 만들어졌다가 그리이스 후기나 로마시대에 와서 Sicily 섬 또는 Nile 강 삼각주라는 해석이 덧붙여졌을 겁니다. 하여간 이 별자리는 Ptolemy
(AD 100~170. 추정. 그리이스계 Egypt 인) 의 Almagest (AD 150) 에 48 개 별자리 중의 하나로 실리게 됩니다. Almagest 에 기록된 별자리 이름은 Trigonon 입니다. 이 단어도 삼각형이란 뜻입니다. 아래 그림은 최초의 근대성도로 불리는
1603 년 Bayer 성도입니다. Ptolemy 의 48 개
별자리 중 하나라서 그런지, 도판전체에 삼각형 하나만 그려 넣고 왕 대접을 해준 것 같습니다. <그림 40 Bayer – Uranometria
(1603). 출처 : 그림 29 와 동일> (3) 남쪽삼각형 – 아빠
찾아 삼만리 남쪽삼각형 자리 (Triangulum Australe) 는 최초 제작자와 위치에 다소 논란이 있는 별자리 입니다. 시대순으로 제작자와 별자리 위치를 정리했습니다. • 남쪽삼각형은 미국대륙과 남반구를 탐사했던 Amerigo
Vespucci (1454~1512. 베스푸치. Italy) 가 1503 년에 쓴 편지에 처음 나타납니다. 그가 묘사한 삼각형 모양 별들 위치는
공작자리 (Pavo) 부근이라고 하므로 지금의 남쪽삼각형 자리 위치와 동일합니다. • 그런데 1589 년에 Petrus Plancius (플란시우스. 1552~1622. 네덜란드) 가 천구를 만들면서 남쪽삼각형 자리 위치를 Argo Navis (아르고호) 바로 남쪽으로 잘못 그려 넣게 됩니다.
• 그 후 1595 년에 남반구 탐사를 떠났던 네덜란드의 Pieter Dirkszoon Keyser (케이저 1540~1596)
와 Frederick de
Houtman (후트만 1571~1627) 이 탐사 후에 새로운 별자리라고 발표한 남반구 12 개 별자리 중에 이 별자리도 포함되어 있습니다. • Plancius 는 1598 년에 다시 천구를 만들었습니다. 여기선
1589 년의 오류를 수정해서 Vespucci
및 Keyser, Houtam 이 묘사한 위치와
같게 되어 있습니다. 이런 이유로 자료에 따라
남쪽삼각형 자리 제작자가 Vespucci, Keyser 및
Houtman 또는 Plancius 등으로 소개되고 있습니다. 지금의 별자리 위치에 따라 정확히 말한다면, 남쪽삼각형 아빠는 Vespucci 가 될 겁니다. 이 별자리가 “맞는 위치” 로 처음 묘사된 것은
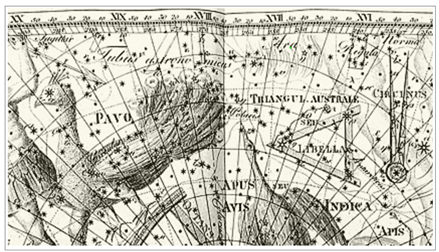
1598 년 Plancius 의 천구입니다. 성도로서는 1603 년 Bayer 성도가 됩니다. Bayer 성도를 포함해서 몇 개 성도를 아래에 올려드립니다. <그림 41 Bayer – Uranometria
(1603). 남쪽삼각형 위치
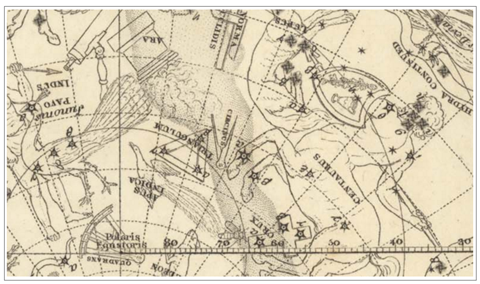
: 가운데 약간 오른쪽. 출처 : 그림 29 와 동일> <그림 42 Bode – Uranographia
(1801) 부분. 남쪽삼각형
위치 : 가운데 약간 오른쪽. 출처 : 그림 29 와 동일> <그림 43 Jamieson - Celestial
Atlas (1822) 부분. 남쪽삼각형 위치 : 그림 가운데
약간 왼쪽. 출처 : ianridpath.com> 성도에 묘사된 별자리 그림 보시면 삼각형, 남쪽삼각형 및 작은삼각형 모두 도형인 삼각형이 아니라 삼각자로 그려져 있습니다. 삼각형은 원래 그리이스 문자 Delta (Δ) 모양으로 만들어졌다가, Sicily 섬 또는
Nile 강 삼각주로 해석되기도 했다고 말씀 드렸습니다. 이후 16 세기 들어 지리상
발견 시대가 되자 항해용 해도 (海圖) 에 사용되는
삼각자로 표현된 것으로 생각됩니다. 별자리
이름인 라틴어 Triangulum 은 영어로 Triangle 또는 Trigon 이며, 이는 도형 삼각형뿐만 아니라 삼각자 뜻으로도 사용됩니다. Hevelius 는 그리이스 시대부터 전해오는 삼각형 자리를 한 개의 삼각자로 생각하고, 일반적으로
사용되는 삼각자 세트가 큰 것과 작은 것 한 쌍임을 감안해서 작은삼각형 자리를 만든 것으로 보입니다. 하지만 그가 이 별자리를 만들었던
1687 년에는 이미 1503 년 Vespucci 기록
및 1598 년 Plancius 천구와 1603 년 Bayer 성도에 표시된 남쪽삼각형 자리가 존재하고 있었습니다. 따라서 밤하늘엔 북반구 삼각형과 같이
삼각자 한 세트가 이미 존재하고 있는 상태였습니다.
이미 지난 일이지만
Hevelius 에게 밤하늘에 자기 흔적을 조금이라도 더 많이 남기려는 욕심을 버리라고 충고하고 싶습니다. 그가 마음을 비웠더라면, 태어났다가 크게 빛도 보지 못한 채 표표히 역사 속으로 사라져간 비운의 별자리 흔적을 바라보는 안타까움은 없었을
것입니다. <끝> 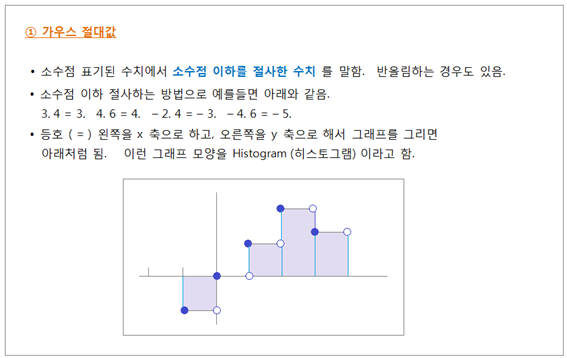















 한담객설 – 청천낙성 담천잡담 월하산책 (9)
한담객설 – 청천낙성 담천잡담 월하산책 (9)
 한담객설 – 청천낙성 담천잡담 월하산책 (7)
한담객설 – 청천낙성 담천잡담 월하산책 (7)