한담객설 2015년 10월 29일 <목 차> I. 청천낙성
– 1 부
우리
존재의 위치 찾기 (4)
(1)
Hubble 이전에
Oepik (Opik) 이 있었다 (2) Oepik
의 나선은하 자전속도와 거리관계 1. 나선은하
자전이란 나선팔 회전이 아니다 2. 자전속도로 거리 구하기 3. Oepik 의 M31 거리 계산과정 (3) Tully
Fisher 의 통계 1. 논문제목은 New
Method, 실제론 Old Method 2. 자전속도와
본래광도의 규칙성 3.
Tully Fisher 논문의 M31 자전속도 검증 II. 청천낙성
– 2 부
나선팔의
정체와 나선은하 자전속도 (1) 나선팔
정체 1. 중력이론 2. 밀도파
이론 3. 기타이론
(2) 은하 구성요소 (별) 자전속도 1. 이론적 계산수치 2. 실제 관측수치 (3) 우리은하
구성요소
(별) 자전속도 (4) 우리은하
나선팔 자전속도 (5) 사람 사는 세상, 별들 사는 은하 1. 태양의 1 년은 ? 2. 태양은
언제쯤 지금의 나선팔을 벗어날까 ? 3. 노년이 되서야 나선팔을 떠나보는 별 4. 얇은 사 (紗) 하이얀 고깔은 고이 접어서 나빌레라 5. 거울이아니었던들내가어찌거울속의나를만나보기라도했겠소 III. 월하산책
잃어버린
별자리를 찾아서 (21) – 프리드리히의
영광 Honores Friderici (1) 문무 (文武) 겸비의 상징 (2) 주극성지역을 고집한
Bode 의 무리수 (3) 양심과 충성심 사이
(4)
Friedrich 2 세의 반응은 어떨지 <본 문> I. 청천낙성 – 1 부
우리 존재의 위치 찾기 (4)
(1) Hubble 이전에 Oepik (Opik) 이 있었다 우주거리에
대한 시리즈로 벌써 네 번째 순서를 올리게 됩니다.
지난 호까진 연주시차, Cepheid 변광성 및 Type Ia 단일축퇴 초신성을 사용해서 거리를 재는 방법을 알아 보았습니다.
이번호에선
나선은하 (Spiral Galaxy) 의 자전속도 (Rotation
Speed) 를 이용해서 그 나선은하까지 거리를 계산하는 방법을 살펴 보겠습니다. 얼핏 생각하면 자전속도와 거리는 관련 없어 보입니다. 하지만 세상만사 복잡해보여도 돌아가는
원리는 간단한 것처럼, 자전속도로 거리를 구하는 것도 기본적 물리법칙이 사용된 것입니다. 이 방법은 1977 년에 처음으로 제시되었다고 알려져있습니다. 그러나 그것은 1922 년에
처음 발표된 방법을 여러 나선은하에 적용한 통계적 수치입니다. 1922 년에 처음 제시된 방법이 기발하기도 하지만, 그보다 더욱 중요한 사항은 산출된 결과가 당시 우주에 대한 개념을 송두리째 바꿀 수 있는 획기적 결과였다는
것입니다. 그러나 이 논문은 주목받지
못하고 그대로 사장 (死藏) 되었고, 이후
그 공적은 다른 사람이 차지하게 됩니다. 1922 년의 해당논문 표지와 초록 일부를 보여 드립니다. 논문링크 주소는 그림 아래에 적어 드렸습니다. <그림 1/2 Ernst Julius Oepik (또는 Opik) 의 논문표지 및 초록 일부 (1922 년). 전체분량 5 pages. 출처 : Harvard 대학교. NASA Astophysics Date System. 미국천문학회 발행 Astrophysical Journal 55.
1922년 6월. articles.adsabs.harvard.edu
논문링크 주소: articles.adsabs.harvard.edu/cgi-bin/nph-iarticle_query ?1922ApJ....55..406O&data_type=PDF_HIGH&whole_paper=YES&type= PRINTER&filetype=.pdf>
위 논문은
Estonia (에스토니아) 국적의 Ernst Julius Öpik (오픽.
1893~1985) 이란 분이 1922 년에 미국천문학회가 발행하는 Astrophysical Journal 에 발표한 것입니다. 내용은 M31 성운까지 거리를 측정한 것입니다. 당시는 M31 은하를 성운으로
불렀습니다. Estonia 철자
Öpik 은 영어표기로 Oepik 또는 Opik 으로
씁니다. 여기서는 위 논문표기대로 Oepik 으로 쓰겠습니다. 이 논문은 분량이
불과 5 pages 이지만, 혁명적 내용을 담고 있습니다. 아래쪽은 위 그림의 초록 (抄錄 Abstract) 중간부분만 별도로 확대한 것입니다. 황색사각형은 M31 까지 거리가 450,000 pc 으로 계산되었음을 나타냅니다. 광년 단위로는 147 만 광년입니다. 지난 한담객설 8월 30일자에서, Hubble 이
1924 년에 발표한 M31 거리는 90 만
광년이라고 말씀 드렸습니다. 현재 인정되고 있는 거리가 254 ± 11 만 광년이므로 실제의
35 % 에 불과합니다 반면에
Oepik 이 발표한 거리는 147 만 광년이므로
실제의 58 % 가 됩니다. Hubble 은 1924 년에 90 만 광년이란 거리를 발표하고 유명인사 반열에 올랐습니다. 하지만 그 보다 2 년 전에 Hubble 보다 더욱 실제에 근접한 결과를 발표한 Oepik 은
왜 기억되지 않을까요 ? 두 분
모두 공식논문은 미국천문학회가 발행하는
Astrophysical Journal 에 실었습니다. 물론 Hubble 은
논문게재 전에 NY Times 에 결과를 싣고, 대중에게
미리 알린 점도 고려될 수 있을 겁니다. 하지만 미국천문학회는 147 만 광년이란 Oepik 의 논문을 게재해 놓고도 주목하지 않았습니다. 그 후 2 년이 지나서 Hubble 이
Oepik 의 거리보다 한참 가까운 거리인 90 만 광년을 발표하자 M31 이 외부은하임이 밝혀졌다고 부산을 떨기 시작합니다. Oepik 은 Estonia 인이며 Estonia 망원경으로 연구했으나, 논문은 미국천문학회 Journal 에 실었습니다. 혹시 그가 미국 천문대에서 연구하는 미국학자였다면 어떤 상황이 되었을지 궁금합니다. (2) Oepik 의
나선은하 자전속도와 거리관계
1. 나선은하 자전이란 나선팔 회전이 아니다 우주거리를 측정하는 모든 방법의 초점은
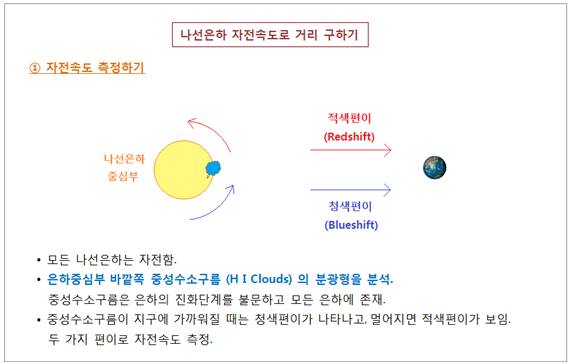
본래광도 (L. Intrinsic Luminosity) 를 알아내는 데 있습니다. Oepik 은 M31 의 자전속도를 이용해서 본래광도를 산출했습니다. 그런데 은하자전이란 용어가 혼동을 일으킬 우려가 있어 미리 정리하고 지나가겠습니다. <그림 3/4 나선은하 자전에 대한 개념> 그런데 나선은하의 자전을 들여다 보면
그 작동원리가 간단치는 않습니다. 별, Gas 구름, 우주먼지 등은 나선은하 내부에서 어디에 위치하는가에 따라 은하중심을 공전하는 속도도 달라질 것입니다. 은하중심부와 외곽지역으로 나누어 속도차이를
정리했습니다. <그림 5 나선은하 중심부와 외곽지역 자전형태> 자전속도를 이용해서 본래광도를 산출할
때는 최대 선속도를 기준으로 계산합니다. 그런데
실제 여러 나선은하 관측결과에 따르면, 중심부의 가장 바깥쪽 선속도가 최대속도이며, 외곽지역 선속도는 위치에 관계없이 중심부의 가장 바깥쪽 선속도와 비슷하게 산출 됩니다. 이런 현상의 원인은 별도로 청천낙성 2 부에서 살펴봅니다. 하여간 은하 중심부가 가장 밝아 관측하기 쉬우므로, 보통 이곳의 가장 바깥쪽 선속도를 측정합니다. 지금부터는 선속도를 그냥 “속도” 로 표기하고, 특별히
각속도와 구분해야 하는 경우에만 선속도 용어를 쓰겠습니다.
2. 자전속도로 거리 구하기 우선 ① 자전속도를 측정하고, ② 자전속도로 질량을 계산한 다음에 ③ 그 질량으로부터 본래광도를 산출합니다.
본래광도를 알게 되면, ④ 안시밝기 (B. Apparent
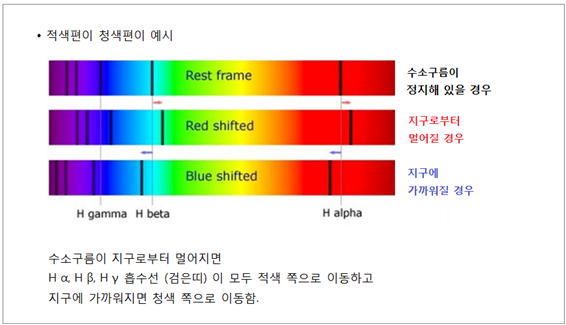
Brightness) 와의 관계식으로 거리 (d) 가 계산됩니다. Oepik 이 사용한 방법의 기본원리는 아래와 같습니다. <그림 6/7/8/9/10/11 나선은하
자전속도를 이용해서 거리를 산출하는 기본개념. 적색청색편이 그림출처 : 영국 Greenwich 천문대. Royal Observatory Greenwich. rmg.co.uk> 한가지 추가 드린다면 태양도 우리은하
중심을 공전하므로 지구도 태양을 따라 움직입니다.
상대편 은하를 관측할 때는 지구의 움직임도 고려해서 상대속도를 구해야 합니다. 태양의 은하중심 공전에 대해선 청천낙성
2 부에서 알아보겠습니다. 3. Oepik 의 M31 거리 계산과정
그러면 위에서 말씀 드린 순서에 맞추어 Oepik 이 M31 거리를 산출하는 과정을 따라가 보겠습니다. ① 자전속도 측정하기 Oepik 은 M31 은하중심부터 시야각거리로 반지름 150 초각 (“), 직경으론
300 초각 지점의 자전속도를 거리계산에 사용했습니다. 이것은 M31 실제크기의 2. 6 % (긴 쪽) 및 8. 3
% (짧은 쪽) 밖에 되지 않는 은하중심부를 관측대상으로 삼은 것입니다. 따라서 고체형 자전할 경우에만 성립하는
위 단락의 수식을 적용할 수 있습니다. 한편
100 초각도 아니고 200 초각도 아닌, 특별히
반지름 150 초각 범위를 대상으로 한 이유는 F.G. Pease 라는
학자의 1918 년 관측자료를 보정해서 사용했기 때문입니다. <그림 2> 를 다시
보시면 M31 의 시야각거리 반지름 150 초각, 직경으론 300 초각 지점 자전속도는 초속 157 km 로 측정되었음을 알 수 있습니다.
② 자전속도로 질량 계산하기
Oepik 은 M31 직경 300 초각 지점 자전속도인 초속 157 km 로 질량을 계산할 때
역시 다른 학자가 측정해 놓은 자료로 M31 직경 300 초각
내부의 질량을 추정했습니다. 그의
논문 일부를 올려 드립니다. <그림 12 Oepik 의 논문일부. 4 page. 직경 300 초각, 자전속도 초속 157
km 인 M31 내부의 추정질량. 출처 : 그림 1/2 와 동일> ③ 질량으로 본래광도 계산하기 및 ④ 안시밝기
측정하고 거리 계산하기 위 인용문에선 직경 300 초각, 자전속도 초속 157
km 인 M31 중심근처 질량이 태양질량의 배수로 표현되어 있습니다. 태양의 본래광도는 이미 알고 있으므로 M31 의 본래광도 (L) 는 <그림
10> 의 “L ∝ M 의 2 승수” 식을 사용해서 구할 수 있습니다. 한편
Oepik 은 태양 및 M31 의 본래광도에 대해
Flux 단위가 아닌, 등급단위를 사용하고 있습니다. 아래 인용문 보십시오. . <그림 13 Oepik 의 논문일부. 4 page. M31 직경 300 초각 내부의 본래광도와 안시밝기 (안시등급). 출처
: 그림 1/2 와 동일> Oepik 은 태양의 안시등급을 – 26. 6 등급이라고
했습니다. 현재 알려진 정확한
등급은 – 26. 74 등급이라 하므로 거의 동일합니다. 또한 인용문에서 보시듯이, M31 직경 300 초각의 안시밝기는 6. 1 등급으로 추정되어 있습니다. 이 부분에서도 Oepik 은 Raynolds 라는 다른 학자의 논문으로 등급을 계산했습니다. 하여간
M31 직경 300 초각 내부의 본래광도 (L) 가
태양 본래광도의 배수단위로 계산되었고, M31 직경 300 초각
내부의 안시밝기 (B) 도 6. 1 등급으로 계산되었으므로
이들을 거리계산식에 대입하면 M31 까지 거리 (d) 가
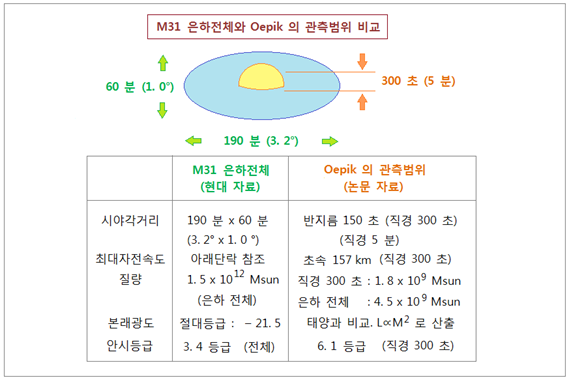
산출됩니다. Oepik 이 M31 거리계산에 사용한 변수들을 아래에
정리했습니다. <그림 14 Oepik 이 M31 거리계산에 사용한 변수와 현대자료 비교> Oepik 의 M31 거리 산출과정에서 보시듯이, Oepik 은 계산에 필요한 대부분의 변수들을 다른 학자들이 산출한 수치를 사용했습니다. Oepik 의 논문분량이 단지 5 page 밖에 되지 않는 이유가
바로 여기에 있다고 보여 집니다. 만일
다른 학자들이 산출한 수치를 수치에 오류가 있다면 계산결과도 달라질 것입니다. 그러나 다른 학자들이 산출한 수치를 사용했다고
해서 자전속도로 거리를 계산하는 방법을 개발해낸 그의 업적이 희석될 수는 없습니다. 하지만 “M31 거리측정” 에 대한 공적을 Hubble 에게 양보한 Oepik 은 1977 년에 또다시 “자전속도로 거리를 계산하는 방법” 마저 다른 사람들에게 선물하게 됩니다. 따라서 요즘의 과학서적에서 “Estonia 천문학자 Oepik” 이란 이름은 찾기 어렵게 되었습니다. 세계 과학계에서도 강대국 또는 과학강국의
논리는 여전히 살아있는 것 같습니다. <그림 15 Ernst Julius Öpik (Oepik. Opik 오픽. 1893~1985. Estonia). 출처 : Armagh Observatory (Ireland 소재). arm.ac.uk> (3) Tully Fisher 의
통계
1. 논문제목은 New Method, 실제론 Old Method 이제는
1977 년에 발표된 논문내용을 살펴 보겠습니다. 우선 표지부터 올려 드립니다. <그림 16 Tully 와 Fisher 의 논문표지 및 초록 일부 (1977 년). 전체분량 15 pages. 출처 : Harvard 대학교. NASA Astophysics Date System. ESO 발행
Astronomy and Astrophysics 54. 1977 년 6월. articles.adsabs.harvard.edu 논문링크 주소: articles.adsabs.harvard.edu/cgi-bin/nph-iarticle_query ?1977A%26A....54..661T&data_type=PDF_HIGH&whole_paper=YES&type= PRINTER&filetype=.pdf 위 논문은 Tully 와 Fisher 가
1975 년에 작성하고 1977 년에 발표한 것입니다. 거리측정 방법은 1922 년에 Oepik 이 발표한 것과 동일합니다. 다만 세월이 흘러 관측기법과 관측속도가 향상되었으므로, 국부은하단과 처녀자리 은하단의 여러 나선은하들 거리를 측정했다는 것과 분광형을 여러 파장영역 (Band) 으로 측정하고 통계를 냈다는 것뿐입니다 (Richard Brent
Tully. 1943~현재. Canada.
James Richard Fisher. 1943~현재. 미국).
이 논문에선 이미 55 년 전에 Oepik 이 처음 개발한 방법이 사용되었는데도 불구하고, 논문 제목이 버젓이 “New Method” 라고 되어 있습니다. 논문 어디에서도 Oepik 이란 이름은 찾을 수 없었습니다. 이들이 만든 그래프는 현재 Tully
Fisher Relation (툴리 피셔 관계) 라는 이름으로 알려져 있고, 거의 대부분 서적이나 자료에서 Tully 와 Fisher 가 이 방법을 개발한 것으로 잘못 소개되어 있습니다. 이미 하늘로 올라간 Oepik 으로선
좀 억울할 일입니다.
2. 자전속도와 본래광도의 규칙성 그러면
Tully 와 Fisher 가 만든 통계는 무엇인지 알아보겠습니다. 아래 도표는 그들이 계산에 사용한 국부은하단
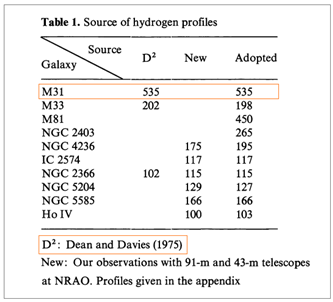
소속 10 개 나선은하의 최대 자전속도 입니다. 도표에서 D2 는 주석처럼
다른 학자의 관측수치이고, New 는 Tully 와 Fisher 가 직접 관측한 수치입니다. 논문의 도표에선 다른 학자들의 수치도 제시되어 있지만, 아래 그림에선 생략했습니다. 이들 수치 중에서 그래프에 적용한 것이
Adopted 수치가 됩니다.
<그림 17 Tully 와 Fisher 논문에 실린 국부은하단 10 개 나선은하 최대 자전속도. 출처 : 그림 13 과 동일. 편집> M31 의 최대 자전속도는 535 km/s 를
적용했음을 알 수 있습니다. 이
수치가 적절히 관측된 수치인지는 바로 아래 단락에서 다시 알아보겠습니다. 이 수치들과 처녀자리 은하단 소속 나선은하들의 자전속도를 합쳐서 그래프로
나타낸 것이 아래 그림입니다. 이들이 계산에 사용한 나선은하들은 1977 년 당시 모두 이미 거리가 알려진 것들 입니다. 따라서 은하 중심부의 본래광도 및 절대등급도 알려져 있습니다. Tully 와 Fisher 가 직접 측정하거나 차용한 은하들의 “최대 자전속도의 log 값” 과
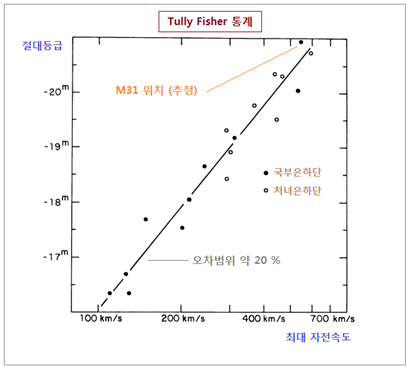
중심부 절대등급을 그래프로 그리면 정비례 관계가 성립됨이 보입니다. 아래 그림의 x 축은 자전속도를 km/s 수치로 나타냈는데, 속도간격을 보시면 간격이 일정하지 않습니다. 그 이유는 x 축 단위가 자전속도의 log 값이기 때문입니다. <그림 18 Tully Fisher 통계. 출처
: 그림 13 과 동일. 편집. 추가> 논문에는 M31 위치에 대해 직접 언급은 없으나, <그림 14> 내용처럼 절대등급 – 21. 6 등급으로 M31 위치를 추정해서 표시했습니다. 그래프 좌표로는 – 21 등급
조금 못미칩니다. 이 그래프 오차범위는 전체적으로 20 %
정도라고 합니다. 하여간
18 개 나선은하에서 이런 규칙성이 보이므로, 다른 나선은하에도
적용할 수 있다는 가정이 성립됩니다. 따라서
어떤 나선은하의 중심부 최대 자전속도만 측정하면 이 그래프를 적용해서 본래광도 (L. 또는 절대등급) 을 알 수 있고, 중심부 안시밝기
(B. 또는 안시등급) 만 측정하면 거리계산식이나
Pogson 방정식으로 거리 (d) 를 구할 수 있게 됩니다.
3. Tully Fisher 논문의 M31 자전속도 검증 여기서
Tully Fisher 논문에 나온 M31 의 자전속도가 현재자료와 어느 정도 일치하는지
살펴 보겠습니다. <그림
17> 보시면 M31 자전속도는 1975 년에 Dean 과
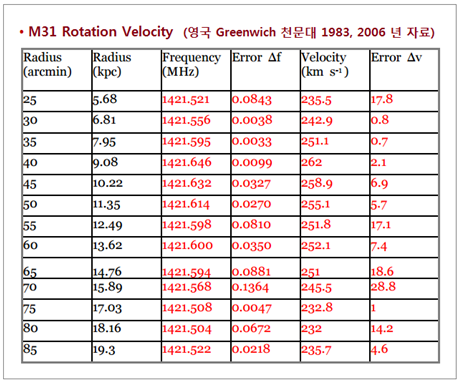
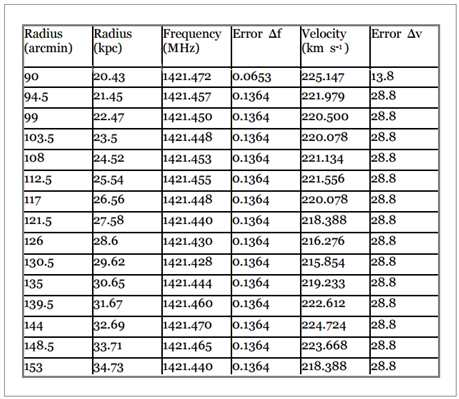
Davies 라는 학자가 측정한 초속 535 km 를 그대로 적용하고 있습니다. 다른 나선은하들은 Tully 와 Fisher 가 직접 관측해서 자료를 얻었지만, M31 은 다른 학자 자료를 사용했습니다. 아마 Dean 과 Davies 의 관측결과를 신뢰한 것 같습니다. 아래 도표는 영국 Greenwich 천문대 웹사이트에 실린 1983 년과 2006 년의 측정자료 입니다. <그림 19-1/19-2 영국 Greenwich 천문대 웹사이트에 게재된 M31 자전속도 측정자료. 출처 : Royal Observatory Greenwich. rmg.co.uk> 도표에서 적색글자는 M31 중심부쪽 50 % 지역이고,
흑색글자는 M31 바깥쪽 50 % 지역입니다. 수치를 보시면 자전속도가 최소 초속 215 km 부터 최대 258 km 사이임을 알 수 있습니다. 자료 중에서 반지름이 가장 짧은 범위가 25 분각입니다.
위 도표에는 관측자료가 없지만, 25 분각보다 더 짧은 반지름에서는 자전속도가 더 느려질 것임이 분명합니다.
중심부는 고체형 자전하므로 반지름이 줄어들면 그 범위의 질량은
더 큰 비율로 줄어들고, 자전속도는 감소하기 때문입니다 (그림
8 참조). 이처럼 Tully 와 Fisher 가 사용한 초속 535 km 속도는 요즘 측정치와 비교했을 때 그들이 인정한 오차범위 20 %
를 훨씬 넘는 수치이므로 “잘못 측정된 것” 임이
분명합니다. 그래프에서 M31 절대등급이 실제와 비슷한 – 21 등급으로 표시된 이유는 이미
알려진 절대등급으로 좌표를 표시했기 때문으로 보입니다. Tully 와 Fisher 의 1977 년 논문은 이후에 여러 가지 버전으로 개량되어 사용되고 있습니다. 이 통계는 나선은하 자전속도를 이용해서 거리를 측정하는 방법을 체계화했다는데
그 가치가 있습니다. 비록 M31 경우와 같은 오류가 보이지만, 도서관 서고에 묻혀있던 1922 년의 방법을 찾아내서 정형화 시킨 공적은 인정되어야 한다고 생각합니다.
다만 논문에서 Oepik 이란
이름을 전혀 언급되지 않은 것은 내내 아쉬운 부분입니다. Tully Fisher
통계는 나선은하에 대해서만 적용 가능합니다. 타원은하도 극히 작은 속도로 자전하지만, 소속 별들이 나름대로 제각각 은하중심을 공전하는 것이므로 규칙성은 없습니다. 또한
나선은하가 너무 멀리 있어 작은 점으로만 확인가능 하다면, 분광분석으로도 자전이 측정되지 않을 것입니다. 분광분석으로 나선은하 자전이 확인되는
한계거리는 보통 10 억 광년이라고 합니다. 따라서 이 보다 먼 거리에 있는 나선은하라면 다른 방법을 써야 될 겁니다. 다음 호에서도 계속 우주거리에 대해 알아보겠습니다. <그림 20 배경그림출처 : 한담객설 2015. 8.16일자 그림 26 과 동일. 편집. 추가> II. 청천낙성 – 2 부
나선팔의 정체와 나선은하 자전속도 (1) 나선팔 정체
1. 중력이론 나선은하는 균형 잡힌 나선팔 때문에 다른
은하에 비해 아름답습니다. 청천낙성 2 부에선 나선은하에 대해 좀 더 자세히 알아보겠습니다. 1 부의 <그림 3> 도
참조해 주십시오. 자기 얼굴을 자기 눈으로는 직접 볼 수
없는 것처럼, 우리은하 모습도 직접 관측할 수는 없습니다. 지금까지는 여러 위성을 통해 우리은하 중심부에 막대 (Bar) 가 있다는 것과 나선팔 (Spiral) 구조가 어느 정도
밝혀졌지만, 우리은하 밖에서 바라본 적은 없으므로 단지 추정에 불과합니다. 만일 거울도 없고 우리 얼굴모습을 비춰볼
연못이나 강물이 없다면, 우리 생긴 모습은 다른 사람 모습으로 추정하는 수 밖에 없습니다. 우리은하 모습도 대부분 이런 과정을 거쳐
확인됩니다. 그런데 우리은하와
같은 종류인 다른 나선은하에서 나선팔이 생기는 과정과 그 운동형태는 아직 속 시원히 밝혀진 것은 없습니다. 인류역사가 수억년이 되었다면 다른 나선은하가 변해가는 과정을 지켜 보았을
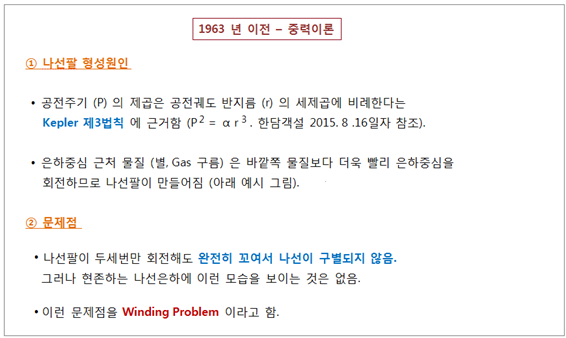
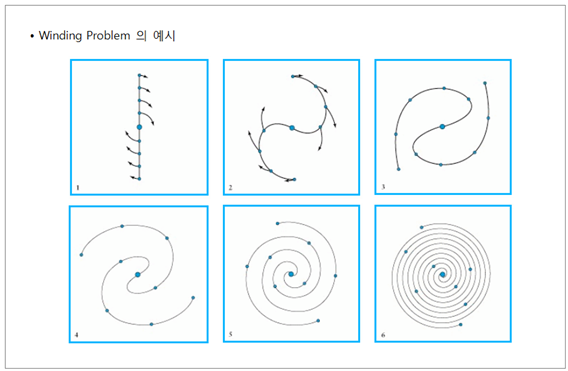
겁니다. 하지만 망원경이 발명된 1608 년 이후부터 따진다면 이제 407 년밖에 지나지 않았으니, 인류가 나선은하 돌아가는 모습을 알아내는 것은 쉽지는 않을 겁니다. 1960 년대 이전까지만 해도 별 같은 은하 구성요소의 상호 중력작용으로 만들어졌고, 그 중력작용으로 나선팔이 점점 더 나선형이 되면서 회전한다고 생각되었습니다. 이런 모형을 나선팔 형성에 관한 중력이론 (Gravitation Theory) 이라고 합니다. 그런데 이런 모형은 나선팔이 두세번만 은하중심을 회전해도 너무 많이 꼬여서
결국 나선구조를 알아 볼 수 없게 됩니다.
이 같은 중력이론의 오류를 Winding Problem 이라고 부릅니다. 말씀 드린 내용을 그림으로 정리했습니다. <그림 21/22 나선팔 형성에 관한 중력이론. 그림출처 : Pennsylvania State University.
astro.psu.edu> 1 번과 2 번 그림에서 화살표 길이차이는
은하중심 물질이 바깥쪽 물질보다 더욱 빠르게 중심을 회전하는 것을 뜻합니다. 나선팔은 결국 6 번 그림처럼
변하게 됩니다.
2. 밀도파 이론
a) 밀도파 의미 위와 같은 중력이론의 모순을 해결하기
위해 등장한 것이 밀도파 이론 (Density Wave Theory) 입니다. 밀도파
(Density Wave) 의 뜻은 은하 구성요소인 별, Gas 구름 등의 동심원 타원궤도
모양을 따서 만들어진 용어입니다. 연못에
돌을 던졌을 때 물이 만들어내는 파장 (Wave) 같이 생긴 것들이 은하공간의 밀도 (Density) 차이를 만들어 나선팔이 생성된다는 의미입니다. 이 이론에 따르면, 나선팔이란
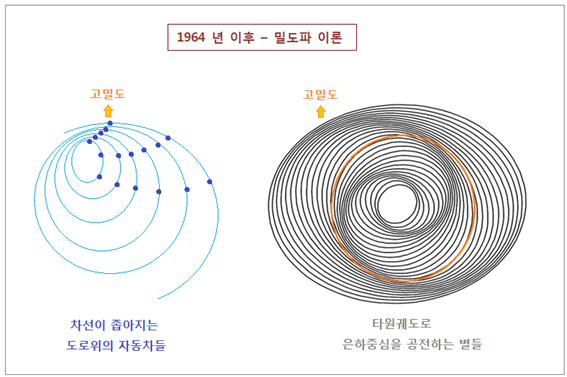
은하 구성요소들이 각기 궤도운동 하다가 어느 지점에서 모이게 되어 물질의 밀도가 높아진 부분을 뜻합니다. 도로 위를 달리는 자동차를 예를 들어
봅니다. 만일 자동차 도로의 어떤
지점에서 갑자기 차선들이 점차 좁아진다면 자동차들은 그 지점에서 밀도가 높아지게 됩니다. 한 개 차가 빠져나가도 뒤에서 다른 차가 계속 진입하므로 좁아진 차선에서의
밀도는 크게 변하지 않습니다. 이런
좁아진 차선자체가 이동한다면 자동차로 밀도가 높아진 지역도 같이 이동하게 될 겁니다. 아래 왼쪽 그림이 이런 상태를 나타냅니다. <그림 23 나선팔 형성에 관한 밀도파 이론. 오른쪽
그림 출처 : 영국왕립학회. Royal Society. rspa.royalsocietypublishing.org> 오른쪽 그림의 타원형 실선들은 크기와
형태가 조금씩 다른 별들의 타원궤도를 나타낸 것입니다.
각각의 궤도마다 수많은 별들이 줄지어 은하중심을 공전한다고 보면, 궤도가 서로
가까워지는 부분에서 별들의 밀도가 높아지게 됩니다.
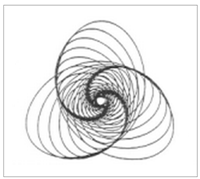
따라서 그 부분은 많은 별들로 인해 주변보다 더욱 밝게 보이므로 멀리서 보면 나선팔로 보이게 됩니다. 위 그림은 나선팔이 두 개인 경우입니다. 그러면 우리 은하처럼 나선팔이 여러 개인
경우, 밀도파 이론에선 궤도가 어떻게 설명되는지 찾아 보았습니다. 나선팔이 많을수록 은하구성요소들의 공전궤도는 더욱 복잡해짐을 알 수 있습니다. <그림 24 나선팔이 여러 개인 경우, 밀도파 이론의 나선팔 형성원리. 출처 : University of Colorado. casa.colorado.edu>
밀도파 이론은 CC Lin 과 Frank Shu 두 분이 1964 년에 발표했습니다. 발표 당시 이 분들은 대학교 학부생 이었습니다. 두 분 모두 각각 중국 북경 (北京) 및 온주시 (溫州市) 에서 태어나 미국으로 이주했습니다.
이 칼럼에서 새로운 천체발견이나 천문이론 관련해서 동양인은 처음 소개되는 것 같습니다
(CC Lin : Chia Chiao Lin. 린쨔차오. 林家翹. 임가교. 1943~2013. Frank Shu : 슈샤셩. 徐遐生. 서하생. 1943~현재).
b) 별의 공전과 나선팔 1964 년에 발표된 밀도파 이론은 중력이론의 Winding Problem 을
해결했으나, 나선팔이 정지상태 또는 움직여도 아주 천천히 회전한다는 전제가 깔려 있습니다. <그림 23> 에서 황색원은 임의의
타원궤도를 선택해서 그대로 그려본 것입니다.
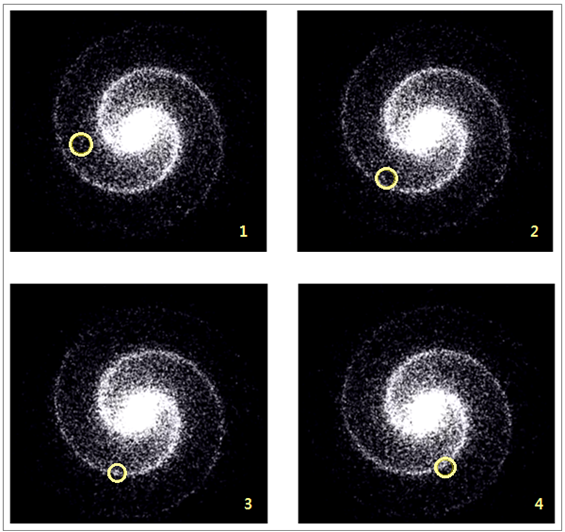
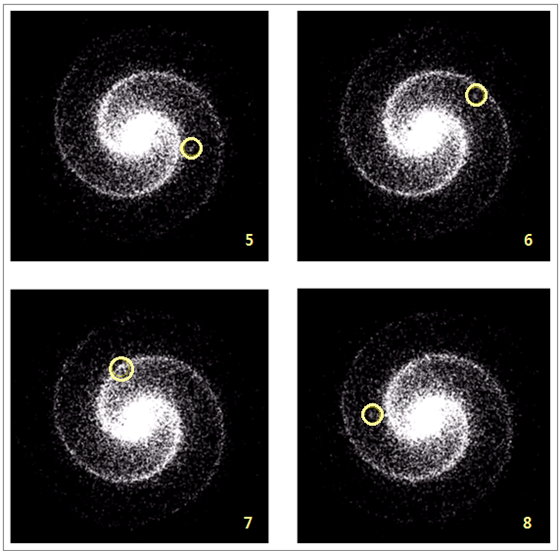
만일 나선팔이 정지해 있거나 또는 황색원을 따라 은하중심을 공전하는 어떤 별보다 회전속도가 느리다면, 그 별은 두 개의 나선팔에 들어갔다 나오는 과정을 반복합니다. 정말 그런지 컴퓨터 시뮬레이션 화면을 여러 개 그림으로 나누어 보여 드립니다. <그림 25-1/25-2 별들이 나선팔에
진입 및 이탈하는 모습을 표현한 컴퓨터 시뮬레이션 화면. 출처 : en.wikipedia.org. 편집. 추가>
노란색
원표시한 부분은 세 별이 위아래로 나란히 늘어선 부분입니다. 이 별들 뿐만 아니라 다른 별들도 나선팔에 들어가고 나오는 과정을 반복합니다. 따라서 이미 만들어진 나선팔 부분에선
계속 높은 밀도가 유지되어 밝게 보이게 됩니다.
그런데 컴퓨터
프로그램을 일부러 그렇게 만들었는지는 알 수 없으나, 세 별이 한바퀴 공전하는 동안 상호 중력작용으로
가까워지고 서로 흡수 합병되는 듯 보입니다.
3. 기타이론 밀도파
이론으로 나선팔의 출생배경은 설명되지만 나선팔 모양이 유지되는 이유와 운동상태를 설명하기엔 부족한 점이 많습니다.
1964년 이후 실제 관측결과, 나선팔 자체도 회전한다는 사실이 밝혀졌습니다. 이 사항은 아래 단락에서 말씀 드립니다. 이런 상황을
설명하기 위해 등장한 여러 이론들은 명칭만 올려 드립니다. 나선팔 형성원인에 대한 이론들이 많다는 것은 한가지 이론으론 설명될 수
없을 만큼 복잡하기 때문일 겁니다. 이들에
대한 추가내용은 그림 아래 웹사이트 주소를 보시기 바랍니다. <그림 26 나선팔 형성에 관한 기타이론. 이론내역 및 그림출처 :
University of Hawaii 웹사이트. 주소 :
ifa.hawaii.edu/~barnes/ast626_05/tss.pdf> (2) 은하 구성요소 (별) 자전속도
1. 이론적 계산수치
1 부에서 나선은하의
자전속도는 나선팔의 회전속도가 아니라, 은하 구성요소인 “별과 Gas 구름들이 은하중심을 공전하는 속도” 라고 말씀 드렸습니다. 또한
<그림 5> 처럼, 은하 중심부분과
외곽지역은 다른 원리로 자전합니다. 이
두 지역의 자전속도를 Newton 의 중력법칙과 이를 응용한
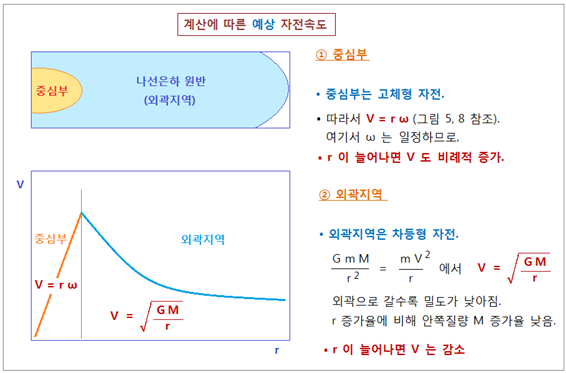
Kepler 제 3 법칙으로 계산해보면 아래 그림처럼 됩니다. <그림 27 나선은하 내부위치별 자전속도
– 이론적 계산에 따른 예상수치> 그림에서 중심부는 레코드 LP 판이나 CD 가 자전하는 것으로 보시면 되고, 외곽지역은 태양계 행성들이 태양을 공전하는 것으로 보시면 됩니다. 따라서 외곽지역에선 중심에서 멀어질수록 나선은하 자전속도는 감소하는 것으로
계산됩니다.
2. 실제 관측수치 그러나 나선은하를 실제로 관측하면 이와
완전히 다른 결과가 나온다고 합니다. 아래
왼쪽 그림은 <그림 19-1/19-2> 의 영국 Greenwich 천문대 웹사이트 M31 자전속도 측정자료를 그래프로
나타낸 것입니다. 중심부분 속도는
관측자료가 없습니다. 오른쪽 그래프는 왼쪽 그래프를 참고해서
예상속도와 실제속도를 비교한 것입니다. 외곽지역에선
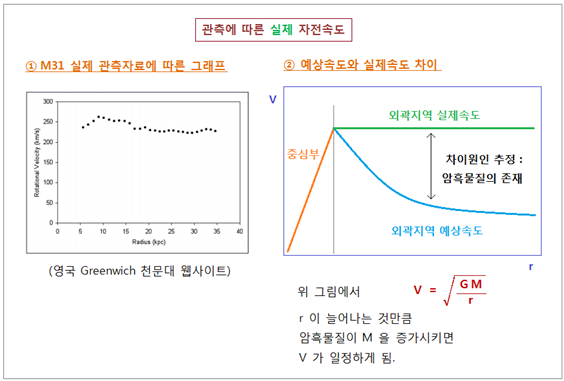
반지름이 늘어나도 속도는 중심부 가장 바깥쪽의 최대속도와 거의 비슷한 최고속도를 유지합니다. <그림 28 나선은하 내부위치별 자전속도
– 예상과 실제 관측수치 비교. 왼쪽 그래프 출처 : 그림 19-1/19-2 와
동일> 이처럼 나선은하 외곽지역에선 반지름이
늘어나도 속도는 중심부 가장 바깥쪽의 최대속도와 거의 비슷한 최고속도를 유지합니다. 실제 관측에 따른 오른쪽 그래프를 은하자전곡선 (Galaxy Rotation Curve) 라고 부릅니다. 그러면 어떻게 Newton 과 Kepler 의 물리법칙에 위배되는 이런 일이 일어날
수 있을까요 ? 학자들의 대답은
“모르겠다” 입니다. 이유를 알 수 없으니, 현재
인류가 가진 모든 관측수단으로도 정체를 밝혀내지 못하는 “어떤 신비한 물질” 이 은하원반 내부에 존재한다고 가정하게 됩니다. 이 신비한 물질이 바로 암흑물질
(Dark Matter) 로 불리는 것입니다. 암흑물질의 질량이 은하 반지름이 늘어나는 비율대로 같이 증가하도록 외곽전체에
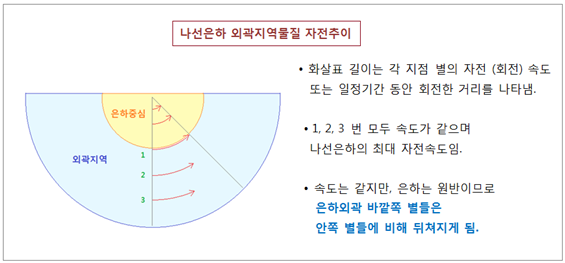
걸쳐 분포하고 있다면, 질량과 반지름 비율이 일정하게 유지되므로 속도도 일정하게 됩니다. 한가지 추가 드린다면, 외곽지역의 자전속도가 거의 일정하다고 해서 중심부 바깥과 보조를 맞추어 회전하는 것은 아닙니다. 나선은하는 도로처럼 직선이 아니고 원반이므로, 외곽지역 속도가 중심부 바깥과 같다면 외곽지역은 중심부에 비해 뒤쳐지게 됩니다. 이런 상황을 그림으로 나타내 보았습니다. <그림 29 나선은하 외곽지역 위치별 자전추이> (3) 우리은하 구성요소 (별) 자전속도 다른 나선은하들은
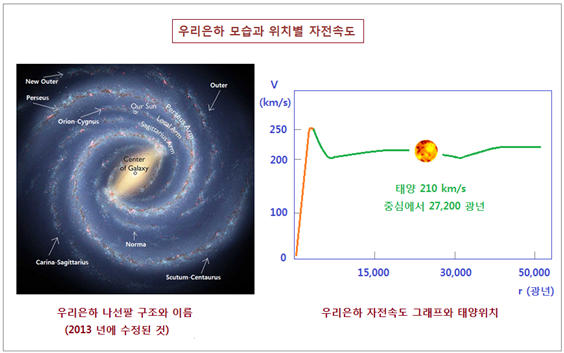
그렇다치고, 우리은하는 어떤 속도로 자전할까요 ? <그림 30 우리은하 내부 천체의 위치별 자전속도. cset.mnsu.edu 등 참조해서 다시 그림. 은하출처 :
Astro News Serial No. 20. Aug. 2013 재인용> 왼쪽 그림은
우리은하 나선팔 구조입니다. 2013 년에
몇가지 새로운 사항이 발견되어 은하 나선팔 모양 및 명칭에 다소 변경이 있었습니다. 자세한 내역은 Astro News
Serial No. 20. Aug. 2013 을 참조해 주십시오. 태양 위치는 그림 위쪽의 Orion-Cygnus
Arm 중간입니다. 태양은
은하중심을 그림에서 시계방향으로 공전합니다. 오른쪽
그림은 위치에 따른 자전속도 그래프 입니다.
기본모양은 M31 경우와 동일합니다. 우리 은하 구성요소의 최대자전 속도는 초속 250 km 가 조금 넘으며, 태양은 초속 210 km 로 움직입니다. (4) 우리은하 나선팔 자전속도 밀도파 이론의 추정은 나선팔이 정지해
있거나 또는 아주 천천히 자전하는 것이지만, 실제로는 어느 정도 속도로 움직입니다. 그런데 우리은하를 포함해서 여러 나선은하의
전체적 나선팔 자전속도 수치는 물론, 나선팔 회전을 유발하는 원인에 대해서도 아직 속 시원하게 알려지진
않았습니다. 아래에 몇 개 자료를
인용 드립니다. 웹사이트 주소는 그림 하단에 있습니다. <그림 31 우리은하중심 막대부분 자전속도에
대한 논문. 2002 년. 편집. 저자
및 출처 : 위 인용내용 참조. 웹사이트 주소 : articles.adsabs.harvard.edu/cgi-bin/nph- iarticle_query?2002MNRAS.334..355D&data_type=PDF_HIGH&whole_paper= YES&type=PRINTER&filetype=.pdf>
제목에서 Pattern Speed 는 나선팔이 움직이는 속도 (Spiral
Pattern Speed) 입니다.
OH/IR stars 는 지난호의 태양부분에서 언급 드린 점근거성 단계
(Asymptotic Giant Branch. AGB) 에 있는 별을 말합니다. 막대부분에선 구성요소인 별과 나선팔이 유사한 속도로 회전한다는 전제 아래, 이런 별을 기준으로 계산한 것으로 추정합니다. 내용을 보면, 막대부분 또는
중심근처 나선팔의 자전속도가 1 kpc (3,260 광년) 진행하는
경우, “초속 59 km” 라고 합니다. <그림 32 우리은하중심 막대부분 자전속도에
대한 논문. 1999 년. 편집.
저자 및 출처 : 위 인용내용 참조. 웹사이트 주소 : iopscience.iop.org/article/10.1086 /312299/fulltext/;jsessionid=D1D00F1EFC4355F1004B52346D3FCA15.c1> 여기서는 막대부분 자전속도가 “초속 53 km” 라고 합니다. 위
논문과 큰 차이 없습니다. 외곽나선팔 자전속도에 대해 밀도파 이론을
제시한 Lin 과 Shu 두 분은 1964 년에 초속 4 km 라는 수치를 제시했습니다. 그러나 외곽지역 어느 부분인지 명시가
없고, 너무 오래된 관측수치라서 인용하지 않습니다. 아래는 외곽나선팔 자전속도에 대한 또 다른 논문초록 (Abstract) 일부입니다. <그림 33 우리은하 외곽 나선팔과 막대부분
자전속도를 비교한 내용. 2010 년. 편집. 저자 및 출처 : 위 인용내용 참조. 웹사이트 주소 : arxiv.org/abs/1003.2489>
위 논문에선 외곽나선팔 자전속도는 막대부분 (Bar) 자전속도 보다 확실히 느리며, 두 부분 자전속도는 서로
상이한 것으로 (decoupled) 추정된다고 합니다. 따라서 외곽나선팔은 초속 53~59
km 보다 느리게 자전하는 것이 됩니다.
(5) 사람 사는 세상, 별들 사는 은하 1. 태양의 1 년은 ?
위 내용을 태양을 기준으로 정리하면, 태양의 자전속도는 초속 210 km 이고, 현재 태양이 머물고 있는 Orion-Cygnus
Arm 자전속도는 초속
53~59 km 보다 느립니다.
참고로 나선팔도 태양과 같은 방향으로 자전하지만 그 방향이 완전히 동일하진 않습니다. 따라서 어느 시점에선 태양이 지금 머물고 있는 Orion-Cygnus Arm 을 벗어날 것임을 예상할 수 있습니다. 그러면 태양은 언제쯤
Orion-Cygnus Arm 을 떠나서 다른 나선팔로 이사갈까요 ? 이를 알아보기
전에 우선 태양이 우리은하를 한바퀴 도는 기간은 얼마나 되는지부터 알아 보겠습니다. 지구가 태양을 한바퀴 돌면 일년이 지나갑니다. 마찬가지로 태양 입장에선 은하중심을 한바퀴
도는 것이 일년이 될 겁니다. 사실
행성들도 태양을 따라다니므로 지구도 은하를 한바퀴 여행하게 됩니다. <그림 34 태양의 은하중심 공전궤도 및 부분확대> 왼쪽 그림의
노란선은 태양의 은하중심 공전궤도를 타원으로 나타낸 것입니다. 배경그림의 우리은하가 상하로 길쭉한 타원이라 태양궤도도 이에 따라 그려
보았습니다. 상세한 자료를 구할
수 없어 임의로 그린 것입니다. 오른쪽은
태양 부근을 확대한 것입니다. 태양은
은하중심에서 27,200 광년 떨어져 있습니다. 태양궤도가 원형이라고 가정하면 공전속도가 초속 210 km 이므로 공전주기는 2 억 4 천만년이 됩니다.
태양에서 살면서 한 살 더 먹으려면 인내심이 조금 필요할 것 같습니다 (태양
원궤도 길이 : 2 x 3. 14 x 27,200 광년 =
170,816 광년. 1 광년 = 9. 4607 x 10 의 12 승수 km. 1 년 = 31,536,000 초. 170,816 광년 ÷ 210 km/s = 2 억 4 천 4 백만년 = 약 2 억 4 천만년). 지난호에서
태양은 45. 7 억년전 만들어지기 시작해서 45. 3 억년전에
핵융합이 시작되면서 주계열성이 되었다고 말씀 드렸습니다. 태양은 그 때부터 지금까지 은하를 19
바퀴나 돈 셈입니다. 앞으로 27 번만 더 돌면, 그 때는 행성상 성운을 거쳐 단독 백색왜성이
되어 있을 겁니다 (향후 65. 205 억년후). 2. 태양은 언제쯤 지금의 나선팔을 벗어날까 ? 이제는
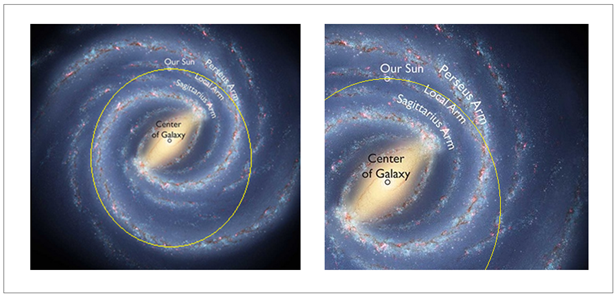
태양이 현재 머물고 있는 Orion-Cygnus Arm 을 벗어나는 시점을 생각해 보겠습니다. 위 위 그림에서 오른쪽 부분확대 보시면
태양궤도는 지금의 나선팔을 건너 빈 공간을 지나 Perseus Arm 을 향해 달려갑니다. 나선팔도 우측 아래 45 ° 방향으로 회전하지만, 속도는 태양보다 많이 느리므로 태양이 나선팔 벗어나는 시점에 큰 영향은 주지 못할 겁니다. 태양이 나선팔을 벗어나는 시기를 계산하려면
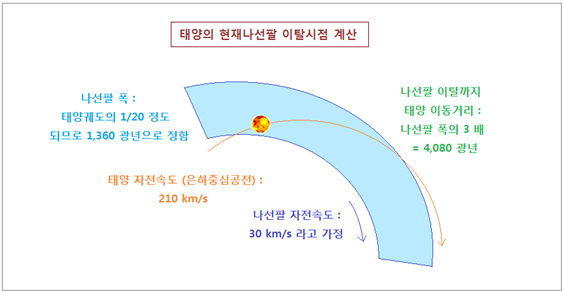
Orion-Cygnus Arm 의 회전속도도 알아야 합니다. 이 속도에 대한 자료는 구하지 못했으므로, 일단 막대부분 속도 53~59 km/s 의 반인 30 km/s 라고 가정하겠습니다. 또한
<그림 34> 로 추정하면, 태양이
위치한 부분에서 Orion-Cygnus Arm 의 폭은
은하중심에서 태양까지 거리 27,200 광년의 1/20 정도
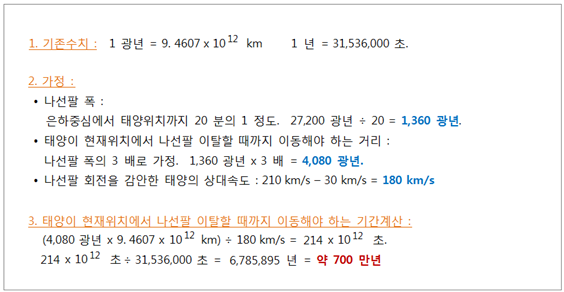
됩니다. 이런 가정에 따라 계산해보면
아래와 같습니다. <그림 35/36 태양이 Orion-Cygnus Arm 을
벗어나는 시점계산> 3. 노년이 되서야 나선팔을
떠나보는 별 그러면
모든 별이 태양처럼 핵융합을 하는 한창 때 여러 나선팔을 들락거릴까요 ? 사람 사는 세상에서도 직업 등의 이유로 젊은 시절부터 여러 곳을 다니는
분들도 있지만, 노년이 되서야 고향을 떠나 먼 곳을 여행하는 분들도 계십니다. 우리은하에 사는 별들도 이와 크게 다르진
않습니다. 어떤 별이
젊었을 때는 나선팔에 계속 머물다가, 늙어서야 나선팔을 떠날 수 밖에 없는 이유는 그 별의 핵융합 기간이
짧기 때문입니다. 예를들어 나선팔
안에서 어떤 별이 태양질량보다 수십배 이상 더 큰 질량으로 태어났다면, 그 별이 핵융합을 할 수 있는
기간은 수백만년 밖에 되지 않습니다. 지금의
태양 위치에서 태양이 나선팔을 벗어나는데 700 만년이 걸리지만 나선팔 진입 경계부근부터는 900 만년 정도 될겁니다. 또한 Orion-Cygnus Arm 은
다른 나선팔에 비해 폭이 좁은 편입니다. 만일
다른 나선팔에서 태어났다면 그곳을 통과하는데 2,000 만년이 걸릴 수도 있습니다. 이 경우, 어떤 별의 핵융합 기간이 수백만년이라면 그 별은 한창 때는 계속 한가지 나선팔에 머물게 됩니다. 이런 별들은
분광형 Type O 또는 Type B 에 속하는 별들입니다. 태양 주변에 이런 별들이 있는지 한 번
찾아 보겠습니다. 아래 그림은 <그림 34> 오른쪽 그림에서 태양주변을 확대한 것으로
보시면 됩니다. Orion-Cygnus
Arm 중간쯤에 태양이 보입니다 <그림 37 Orion-Cygnus Arm 내부 별들 위치. 출처 : Astro
News Serial No. 20. Aug. 2013 재인용. 그림 : Richard Powell. 편집> 위 그림에
보이는 별들의 분광형은 아래와 같습니다.
Type O, Type B 별들 위치를 확인해 보시기 바랍니다. • Type O :
Alnitak, Mintaka, α Cam (기린) • Type B :
Alnilam, Rigel • Type A :
η Leo (사자). κ Cas (카시오페이아). • Type F :
δ CMa (큰개), Polaris,
γ Cyg (백조). • Type M :
Betelgeus. μ Cep (세페우스). • 미확인 :
ρ
Cas. Orion Belt 세 별과 Rigel 은 Type O,
Type B 이고, 기린 가슴부분 알파별도 Type O 입니다. 이들 다섯개 별들 모두 수백만년 후에는
초신성 폭발 합니다. 그 중에서 Rigel 은 700~900 만년 후에 폭발한다고 하므로 다른 별들
보다 좀 늦은 편입니다. 태양이
나선팔을 벗어나는 시점이 700 만년 후이므로, Rigel 이
핵융합 활동하는 시기의 대부분은 Orion-Cygnus Arm 에 머문다고 할 수 있습니다. 참고로 Betelgeus 는 현재 적색초거성이며 분광형은 Type M 입니다. 지금의
Betelgeus 를 태양위치에 가져다 놓으면 외피가 목성궤도까지 도달합니다. 태양이 적색거성이 될 때는, 외피가
화성궤도에 조금 못미칩니다.
Betelgeus 는 초신성 폭발하지 않는다는 학설이 지배적인 듯 보입니다. 대신에 내부물질이 끓어올라 거품
(Bubble) 형태로 우주로 방출된다고 합니다. 나선팔
내부는 많은 별과 Gas 구름 때문에 밀도가 높아 압력이 높습니다. 따라서 새로운 별들이 태어나는 공간이 되며, 이런 이유로 나선팔은 별들의 요람이라고 불립니다. 그러나 태양주변 Type O 와 Type B 별들처럼, 태어날 때 너무 큰 질량을 갖고 태어나면 젊었을
때 다른 나선팔 구경은 못할 수도 있습니다.
그렇더라도 화끈하게 초신성 폭발하고 난 후, 중성자성 또는 블랙홀이 되어선
무한에 가까운 긴 시간동안 여행할 수 있을테니 그리 섭섭하진 않을 겁니다. 4. 얇은 사 (紗) 하이얀 고깔은 고이 접어서 나빌레라 토막상식
두 개 알아보면서 청천낙성 마무리할까 합니다.
우리은하 직경은 10~12 만 광년입니다. 긴 쪽의 부분이 18 만 광년에
달한다는 자료도 있습니다. 그러면
관측된 은하 중에서 직경이 가장 큰 나선은하는 무엇일까요 ? 아래 사진 보시지요. <그림 38 NGC 6872. 출처 : commons.wikimedia.org.
ESO/VLT> 그림의
나선은하는 NGC 6872 입니다. 남반구 공작자리 (Pavo) 에
있습니다. 오른쪽 상단 렌즈형은하는 IC 4970 입니다
NGC 6872 의 양쪽 나선팔 끝까지 거리는 52. 2 만 광년이라고 하므로
우리은하 직경보다 무려 5 배나 더 큽니다. 이 은하 중심부가 우리은하 크기외 비슷할 겁니다. 이 은하는
콘돌 (Condor) 이 날개를 펴고 날아가는 모습이라고 해서 콘돌은하로도 불립니다. 콘돌은 중남미에 사는 독수리입니다. 이 은하가 남반구에서 보이기 때문에 이런
이름이 붙었을 겁니다. 만일 우리나라에서
이 은하가 보인다면 어떤 이름이 되었을지 생각해 보았습니다. <그림 39 승무 (僧舞). 출처 :
m.cafe.daum.net> 위 그림은
승무 (僧舞) 모습입니다. 승무 추는 분의 소매팔이 NGC
6872 나선팔과 닯았습니다.
소제목은 조지훈 (趙芝薰. 1920~1968) 시인의 시 “승무” 일부분입니다. 가까운 미래에 “승무은하” 같은 우리말 이름 은하를 불러볼 수 있기를 기대합니다. 5. 거울이아니었던들내가어찌거울속의나를만나보기라도했겠소 지금까지
관측된 은하 중에서 우리은하와 가장 닮았을 것으로 추정되는 은하는 M83 입니다. 이것은
NGC 5236 또는 남쪽바람개비 은하 (Southern Pinwheel Galaxy) 로도
불립니다. 바다뱀자리 (Hydra) 에 있습니다. 모습은 우리은하와 비슷할지라도, 직경은
우리은하의 반인 5. 5 만 광년에 불과합니다. <그림 40 M 83 (NGC 5236).
출처 : commons.wikimedia.org. ESO/VLT> 소제목의
시는 이상 (李箱. 본명 김해경. 金海卿 (1910~1937) 의 “거울” 이란
시의 일부 입니다. 원문 시 그대로
띄어쓰기를 하지않고 적었습니다. 우리은하가
이상의 시를 알고 있다면, 이렇게 중얼거릴지도 모르겠습니다. “M83 이 아니었던들 내가 어찌 거울 속의 나를 만나보기라도 했겠소” III. 월하산책
잃어버린 별자리를 찾아서 (21) – 프리드리히의
영광 Honores Friderici (1) 문무 (文武) 겸비의 상징 제목만
보셔도 짐작되시는 것처럼, 이번에 알아볼 별자리는 Friedrich
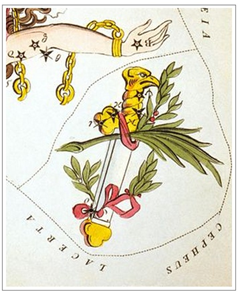
2 세 (프리드리히) 라는 왕에게 바쳐진 것입니다. 우선 채색성도의 별자리 모양부터 보겠습니다. <그림 41 Jehoshaphat Aspin –
Urania’s Mirror 일부. 1825. 영국. 수작업
채색. 출처 : commeons.wikimedia.org>
이런저런
장식이 있어 혼란스럽지만, 이 별자리는 칼을 그린 것입니다. 독수리
머리부분이 손잡이가 됩니다. 별자리
소속 별은 5 개가 보입니다. 리본으로 장식된 나뭇잎은 월계수 (月桂樹 Laurel) 잎입니다. 고대 그리이스의 올림픽 경기 우승자에게 월계수 잎을 엮어
월계관 (Laurel Wreath, Laurel Crown) 을 씌워주던 전통에 따라, 월계수 잎은 명예와 영광의 상징이 되었습니다. 그런데
칼 가운데 부분 파 줄기처럼 생긴 것은 무엇일까요 ?
모양은 어떤 식물줄기 같아 보이지만, 이것은 새털깃대 펜 (Quill Pen) 입니다. 칼과 펜은 “문무 (文武) 를 겸비” 했음을
뜻합니다. 세계 역사에서 칼로
일어선 왕은 많으나, 사가 (史家) 들로부터 문무를 겸비했다고 인정되는 왕은 몇 되지 않을 겁니다. 그 중에서도 지금 독일의 전신 (前身) 인 프로이센의 Friedrich 2 세 는 문무 뿐만 아니라 음악적 재능까지 겸비한 왕이었습니다. 참고로
프로이센은 독일어 표기로 Preußen (프로이센) 으로 쓰며, 영어표기로는 Prussia (프러시아) 라고합니다. 프리드리히 왕은 독일어로 Friedrich II (프리드리히
2 세) 로 쓰고, 영어로는 Frederick II (프레데릭 2 세) 라고 합니다.
생존은 1712~1786 이며 재위기간은
1740~1786 입니다. 이 왕에
대해선 현재 독일의 기반을 만들었다고 중학교 역사시간에도 배운 기억이 납니다. 당시 국가기반 형성은 당연히 군사력 증강과 전쟁을 통한 영토확대입니다. Friedrich 2 세는 강력한 군사지도자였지만, 한편으론 훌륭한 Flute 연주자였고 작곡에도 재능을 보였습니다. 그는 교향곡 네 개와 백 개가 넘은 Flute Sonata 를 남겼다고 전해집니다. 또한 당시 유행하던 계몽주의
(Enlightment) 영향으로 철학자 황제로 불리는 로마의 Marcus Aurelius (마르쿠스
아우렐리우스) 황제를 존경하고, 프랑스 절학자 Voltaire 와 교류했다고 전해 집니다. 이런 면모를 보면, 칼과 새털깃대
펜이 같이 그려진 것이 어색하진 않습니다. (2) 주극성지역을 고집한 Bode 의 무리수 이 별자리는
매번 성도를 인용드리는 Johann Bode (1747~1826. 독일) 가 1787 년에 만든 것입니다. 1787 년은 Friedrich 2 세가
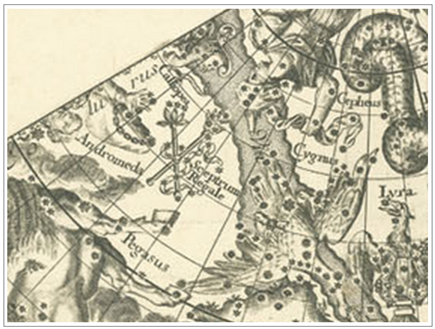
사망한 다음 해로, Bode 는 그의 저서에서 이 별자리를 만들어 소개했습니다. 성도그림으로 처음 묘사된 것은 1792 년에 프랑스어로 출판된 아래 책자입니다. 이 책의 내용일부와 Friedrich
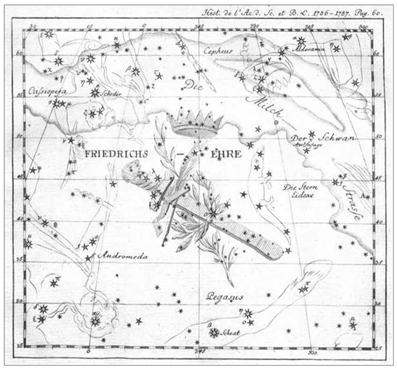
2 세 별자리 그림을 보여 드립니다. <그림 42/43 Bode 의 Friedrich 2 세 별자리 그림이 처음 실린 책과 성도 (1792). 책
이름 : Mémoires de l'Académie Royale des Sciences et
Belles-Lettres. 출처 : bibliothek.bbaw.de> 별자리
이름은 라틴어가 아니라 독일어인 Friedrichs Ehre (프리드리히 이허) 로 되어있습니다. Ehre 는 우리말로 명예 (Honor) 또는 영광 (Glory) 입니다. Bode 가 이 별자리를 만들 때는 왕관까지
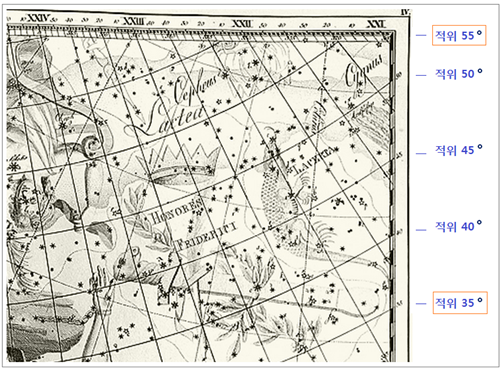
그려넣었습니다. <그림 44 Bode 의 Uranographia (1801). 출처 : Tartu Observatooriumi Virtuaalne Muuseum> 위 성도는 Bode 의 체계적 성도인 1801 년 Uranographia 입니다. 별자리 이름이 라틴어인 Honores Friderici 로 바뀌어 있습니다. 이
별자리의 적위범위가 35° ~ 55° 사이 임을 살펴보시기 바랍니다. 아래 그림은
영국의 Alexander
Jamieson 이 1822
년에 발행한 성도입니다. 여기선
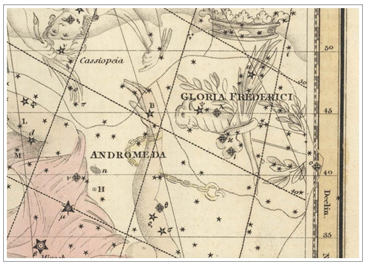
이름이 다시 Gloria Frederici 로 변경되었습니다. <그림 45 A. Jamieson -
Celestial Atlas (1822). 출처 : ianridpath.com> 이 별자리
위치는 Andromeda 와 도마뱀 (Lacerta) 사이
입니다. 도마뱀은 1687 년에 Hevelius 가 만든 것으로 그의 1690 년 성도에 처음 등장합니다. Hevelius 는 Andromeda 와 백조 (Cygnus) 사이 공간에 도마뱀을 새로
만들어 넣어습니다. Bode 는
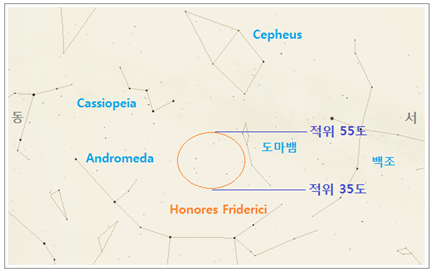
주극성 지역에서 가깝고 남는 공간을 찾아다니다가, 결국 도마뱀 동쪽 좁은 공간에 Friedrich 2 세 별자리를 끼워 넣은 듯 보입니다. Bode 성도 <그림 44> 의 적위와 아래 현대성도를 비교해 보시기 바랍니다. <그림 46 현대 성도에서 Friedrich 2 세
별자리 (Honores Friderici) 위치. 출처 :
Stellarium 화면. 편집. 추가> 이 별자리의
적위는 35° ~ 55° 입니다. 서울의 위도를 N 37° 로 본다면, 서울에서의 주극성 적위범위는 90° ~ 53° 가 되므로, 이 별자리 거의 대부분이 주극성이 되지
못합니다. 그러면 독일에선 어떨까요 ? 아래는 현재 독일영토의 위도범위와 그
지역에서의 주극성 범위 입니다. 참고로
주극성 적위범위는 90° ~ (90° – 위도) 입니다. • 독일 최북단 : N 55° 주극성 적위범위 : 90° ~
35° 전체가 주극성. • Berlin : N 52° 주극성 적위범위 : 90° ~ 38° 3° 만큼 출몰성. • 독일 최남단 : N 47° 주극성 적위범위 : 90° ~
43° 8° 만큼 출몰성. Friedrich 2 세 별자리의 적위가 35°~55° 이므로, 독일북부에선 전체가 주극성이고, 수도 Berlin 에선 거의 대부분이 주극성이며, 남부에선 일부만 출몰성이
됩니다. 주극성 지역은 동양천문도에서 자미원 (紫薇垣) 으로 불립니다. 이 지역의 별들은 계절이나 시간에 상관없이
항상 밤하늘에 보이기 때문에 동서양 모두에서 왕의 상징이나 왕의 거처로 여겨졌습니다. Bode 는 왕의 신분에 맞는 주극성 지역에
별자리를 만들려 했던 것으로 보입니다. 그러나
주극성 지역은 당시에도 이미 만원이라 적당한 빈자리는 없었습니다. 자리 찾기에 고심하던 Bode 는
결국 무리수를 쓰면서까지 별자리를 만들게 됩니다. (3) 양심과 충성심 사이
Bode 가 선택한 자리는 그가 1787 년에 Friedrich 2 세 별자리를 만들기 이전에 이미 다른 별자리가 차지하고 있던 곳입니다.
그 별자리는 프랑스의
Augustin Royer (오귀스땡 후와예. 생존연대 미확인) 가 만든 것인데, 그가 살았던 시대의 왕이었던 Louis (루이) 14 세
(1638~1715) 를 위한 것입니다.
별자리 이름은 Sceptrum Régale (셉트훔므 헤갈르) 이며, 영어로는
Royal Scepter (로얄 셉터) 로 부릅니다. Scepter 는 왕이 권력의 상징으로 들고 다니는 지팡이인 홀 (笏) 이므로, Royal Scepter 는 왕의 홀이 됩니다. 지난
황도12궁 시리즈에서 Sumer 의 Old Babylonia 시대에 만들어진 Nergal (네르갈) 석상
Mace 에 대해 말씀 드린 적 있습니다. 이 Mace 는 Egypt, 그리이스 및 로마를 거쳐 지금의 서유럽에 Scepter 로
전해지고 있습니다. 기억나시도록 Nergal 석상모습 다시 보여 드립니다. <그림 47 Nergal 부조. Old Babylonia 시대. BC 2100~BC 1500 년경. 영국 Oxford 소재 Ashmolean 박물관 소장. 출처
: 브리태니커 백과사전. britannica.com. 한담객설 2014. 11. 20 일자 재인용> 그러면 Louis 14 세의 Scepter 는 어떻게 생겼을까요 ? <그림 48 Louis 14 세의 Scepter. 출처 : 왼쪽 commons.wikimdia.org. 화가 : Hyacinthe Rigaud. 제작 1701 년. 오른쪽 : artflakes.com. 화가 : Henri
Testelin. 제작
1668 년. 편집> 위 그림은 Louis 14 세 초상화에 보이는 Scepter 두 종류입니다. 왼쪽은 짧은 형태인데, 아래쪽이 머리부분입니다. 오른쪽은 길이가 사람 키 만한 것입니다. Augustin Royer 의 본래 직업은 건축가였다고 합니다. 천문학에도 관심이 있었는지, 1679 년에
성도를 발행했으며 그곳에 Sceptrum Régale 별자리가 실렸다고 합니다. 그가 발행한 성도는 찾지 못했습니다. 대신 1724 년에 Johann Ludwig Andreae 가 발행한 성도를 보여 드립니다. 아래 성도에서 중간쯤에 십자가처럼 생긴
것이 Sceptrum Régale 입니다. 성도
그림에서 한 개는 초상화의 Scepter 와 같아 보이지만 다른 한 개는 조금 다른 것 같습니다. <그림 49 Johann Ludwig Andreae 성도의
Sceptrum Régale (왕의 홀) 별자리. 1724 년 발행. 출처 : crouchrarebooks.com Bode 가 만든 별자리와 Augustin Royer 가 만든 별자리를 비교해
보았습니다. • Augustin Royer (프랑스) 의
Sceptrum Régale : 1679 년 제작. 프랑스 왕 Louis 14 세
상징. • Johann Bode (독일) 의 Honores Friderici : 1787 년 제작. 독일 왕 Friedrich 2 세
상징. 성도와
비교 표에서 보시듯이, Bode 는 그 보다 108 년 전에
먼저 만들어진 별자리를 지우개로 깨끗이 지워버리고, 똑같은 위치에
Friedrich 2 세 별자리를 그려 넣은 것을 알 수 있습니다. <그림 45> Alexander Jamieson 의 1822 년 성도는 전체적으로 1801 년 Bode 성도를 따른 것입니다. Bode 가 만든 것이나 Augustin Royer 가 만든 것이나 모두 자국
왕의 상징 별자리 입니다. 비록 Augustin Royer 의 직업이 건축가이며 프로 천문학자가 아닐지라도, 이미
존재하는 인접국가 왕의 별자리를 없애버리고 자기나라 왕을 위한 별자리를 그려 넣은 것이 학자로서 양심에 맞는지 의심스럽습니다. 여담 한마디
드리면, 조선시대에 왕의 묘소는 한양에서 거리가 100 리 (里) 안에 만들어져야 했습니다. 100 리는 약 40 km 입니다.
그런데, 한양중심으로 반경 40 km 내부에
소위 명당자리는 거의 대부분 기존에 한양에 터잡고 살던 사대부들 조상묘소였습니다. 따라서 조선 중기 이후로 갈수록 점점 왕의 묘소 쓸만한 자리가 부족하게
됩니다. 결국 어떤 사대부집안의
기존 묘소가 쓸만하면, 그 묘소를 이장시키고 그 자리를 왕의 묘소로 쓰게 됩니다. 이미 다른 사람이 차지하고 있는 묘자리를
왕이 사용하는 것입니다. 이런 경우, 이미 다른 혼령이 머물던 자리를 왕이 사용하는 것일까요 ? 조선시대엔 사대부를 비롯한 일반 사가
(私家) 의 장법 (葬法) 과 왕가 (王家) 의 장법에는 몇가지 구별이 있었습니다. 그 중에서 대표적인 것이 일반인 묘소는 10 자 (약 3 m) 이상
깊이로는 팔 수 없도록 했지만, 왕의 묘소는 20 자 (약 6 m) 이상으로 훨씬 더 깊게 파는 것입니다. 따라서 묘소를 지나는 지기 (地氣, 땅의 기운) 가
서로 다르므로 왕이 양반이 쓰던 자리를 다시 사용한다는 개념은 아니라고 합니다. 아파트에 비유하면, 왕이 이미
입주해 살던 일반인을 모두 쫒아내고, 옥상에 새로 펜트하우스를 지어서 입주하는 형국입니다. 그러면 아파트 주소 “번지 수” 는 같더라도 같은 집에 산다고는 볼 수 없습니다. 그런데
이런 관례가 정적 (政敵) 을 괴롭히는 수단으로 악용되기도 했습니다. 어떤 왕이 사망했을 때, 상대방 정적의 집안을 초토화 시키려면 정적의 어떤 조상 묘가 가장 명당이라고 힘있는 왕족 (대비 등) 에게 선전하는 것입니다. 묘자리 선정하는 담당관리까지 나서서 그 자리가 제일 좋다고 추천하면, 그 왕릉이 들어서는 넓은 지역의 모든 묘소 및 가옥, 전답들은 이전해야
합니다. 조상 묘소들을 이장하고
이사까지 해야하는 당사자들로서는 불평 한마디 할 수도 없는 괴로운 일이었을 겁니다. (4) Friedrich 2 세 반응은 어떨지 한편, 독일과 프랑스는 그 당시에도 영토문제로 분쟁관계였습니다. 그러나 Bode 가 별자리를
헌정한 Friedrich 2 세는 적대관계일지라도 프랑스 문화는 존경했습니다. 그가
Voltaire 와 교류한 것은 위에서 말씀 드렸습니다. 또한 그는 Berlin 근처 Potsdam (포츠담) 에
Sanssuci (상수시) 궁전을 새로 세우고 그곳에서 자기가 작곡한 Flute Sonata 발표회도 많이 열었습니다. 그런데
그가 작명한 궁전 이름 Sanssouci 는 독일어가 아니라 프랑스어 입니다. Sans (상) 은 “없다” 뜻이며, Souci (수시) 는 “근심, 걱정” 입니다. 따라서 근심 없는 궁전 뜻이 됩니다. 기독교식으로 말하면 요단강 건너편 궁전이 되고, 불교식으로 말하면 피안궁 (彼岸宮) 또는 무색계 (無色界