Astro News Serial No 19. Vol No II
July 2013
<목 차>
I. Life with Kaas
기조력 – 오묘한 물리법칙의 내면
(1) 청춘, 거울 그리고 바다
(2) 기조력 접근방법론
1. 용어 정리
2. 원심력+중력과 중력차이
(3) 중력차이 이론
1. 지구표면 각 지점에 작용하는 중력차이
2. 기조력 크기 수치화
(4) 원심력+중력 이론
1. 지구표면 각 지점에서 달이 지구에 미치는 중력 차이
2. 지구표면 각 지점에서 생기는 원심력
a) 지구자체 중심과 지구-달 질량중심의 운동궤적
b) 지구표면 위의 원심력
3. 지구표면 위의 원심력과 달의 인력의 합계
(5) 태양의 기조력과 달의 기조력 차이는 얼마나 될까 ?
(6) 조석변화에 영향을 주는 천문학적 요인들
1. 달의 위상 변화 (Lunar Phase Effect)
2. 공전궤도상 거리 (Orbital Distance Effect)
3. 달 공전궤도 기울기 (Lunar Declination Effect)
a) Semidiurnal Tide
b) Mixed Tide
c) Diurnal Tide
(7) 밀물, 썰물시간이 매일 조금씩 차이가 나는 이유
1. 달이 고정되어 있을 경우
2. 달도 공전운동 할 경우
(8) 2013년 7월의 인천 앞바다 물때표
II. Not Essential But Beneficial
Roche’s Limit (로쉬의 한계) – 가까이 오면 다친다 !
(1) It’s non of my business ?
(2) 슈메이커-레비 9 혜성의 경우
(3) 지구와 달의 경우
(4) 로쉬의 한계 구하기
1. 로쉬의 한계 공식
2. 지구와 달의 로쉬의 한계
3. 목성과 슈메이커-레비 9 의 로쉬의 한계
III. Coffee Break
1 분각, 1 초각은 어느 정도 크기일까 ?
(1) 각거리를 표시하는 기호들
(2) 100원 동전으로 계산한 각거리
IV. Surprise & Mystery
W49B – 우리은하 최연소 블랙홀
(1) 우리은하 20 번째 블랙홀
(2) 1,000 살이 최연소 ?
V. Journey to Deep Sky
잃어버린 별자리를 찾아서 (7 회)
Turdus Solitarius 와 Noctua (지빠귀자리와 올빼미자리)
(1) Turdus Solitarius 가 사는 곳
(2) 지빠귀 정체에 대한 논란
(3) 그리이스 신화의 <아테나 여신 올빼미 (Athena Noctua)>
(4) 로마 신화의 <미네르바 부엉이 (Minerva Noctua)>
(5) 밤하늘의 아홉 마리 새들
VI. Moon River Wider Than a Mile
Apollo 11 호 우주비행사 Crater 찾기
(1) 고요하지만은 않은 고요의 바다 주변
(2) 아직도 우리는 한 팀 - Armstrong, Aldrin, Collins
(3) 고요하게 사시는 귀하신 분 Lamont
(4) 위대는 평범이외다
<본 문>
I. Life with Kaas
기조력 – 오묘한 물리법칙의 내면
(1) 청춘, 거울 그리고 바다

<그림 picstopin.com >
날도 더우니 시원하시라고 바다 사진 먼저 올려 드린다. 바야흐로 7월, 여름휴가의 계절이다. 여름은 청춘의 계절이고, 휴가라 하면 산 보다는 바다가 먼저 연상된다. 바다는 청춘들이 그동안 갈고 닦은 식스팩과 에스라인을 뽐낼 수 있는 장소이기도 하다. 저는 비록 식스팩은 없으나 그래도 바다는 아무때고 좋다. 민태원의 수필 <청춘예찬>에 나오는 “청춘 ! 이는 듣기만 하여도 가슴 설레는 말이다” 처럼 아직도 바다” 란 단어를 듣기만해도 가슴이 뛴다.
하지만 좀 더 찬찬히 생각해보면 <청춘예찬> 같은 영탄조 (詠歎調) 보다는 서정주의 <국화 옆에서> 가 제 분위기에 더 맞을지도 모르겠다. “그립고 아쉬움에 가슴 조이던 머언 먼 젊음의 뒤안길에서 이제는 돌아와 거울 앞에 선 내 누님같이 생긴 꽃이여” 에 나오는 “거울” 을 “바다” 로 바꾼다면 주제파악 제대로 한다는 소리 들을 것 같다. 사실 마음만은 이팔청춘이라고 아직도 입으로 주절거리지만 그 시대는 지났다는 것을 깨달아야 비로소 철 들었다는 소리 들을 것이다.
참고로 위에 언급드린 두 분은 정도 차이는 있으나 모두 친일문학가라는 비난이 있어 제가 인용한 글 모두 고등학교 국어교과서에선 이미 오래전에 삭제된 것으로 기억한다. 그러나 여기서는 주제가 문학이 아니라 아마추어 천문학이므로 인용을 양해해 주시기 바랍니다.
바다의 밀물과 썰물을 언급드리려다 뜬금없이 <청춘예찬> 이나 <국화 옆에서> 를 인용하고 있으니 너무 멀리 나온 것 같다. 기왕에 한 말씀 더 드린다면, 어디서나 길어야 수시간 차로 달려가면 바다를 볼 수 있는 우리나라는 축복받은 나라이다. 예를 들어 미국 중부지방에 사는 사람이 바다를 보고 싶을 경우에 달려가야 하는 거리를 한 번 생각해 보시면 이해 되시리라 믿는다.
하여간 바다에는 지역에 따라 그 규모차이는 있으나 모두 밀물과 썰물이 있고, 이는 <기조력> 또는 <조석력> 때문이라는 것은 잘 아실 것이다. 저는 꽤 오래전에 우리나라 인천 앞바다에서 밀물이 일어날 때 우리나라 반대편 (대척점) 인 남미 Urguay 앞바다에서도 밀물이 일어난다는 사실을 알고나서 무척 신기하게 생각했었다.
또한 Shoemaker-Levy 9 혜성 (공식명칭 D/1993 F2) 이 목성과 충돌하기 전에 여러조각으로 깨진 것이라던가, 목성 위성인 Io 의 화산활동, 토성 고리의 형성, 상호작용 은하들의 뒤틀림 현상 등이 모두 기조력 때문이라는 말은 많이 보아 왔지만 그 기조력 자체에 대한 설명은 여러 자료를 찾아 보아도 쉽게 이해되지는 않는다. 사실 머나먼 목성과 혜성 사이의 “조석력” 은 차치하고라도 우리 코 앞에 있는 인천 앞바다 “조석현상” 시간을 자세히 아시는 분은 어부나 프로급 조사 (釣士 – 낚시인) 아니면 드물 것이다.
여기서는 기조력 또는 조석력에 대해 제가 접근 가능한 정도까지만 살펴보고 밀물, 썰물의 원인및 현상에 대해서도 같이 알아보려 한다. 나아가서 소위 <로쉬의 한계> 라 부르는 물리적 현상에 대해서도 바로 다음 칼럼 <Not Essential But Beneficial> 에서 간단히 짚어보겠다. 칼럼 쓰는데 참고한 자료중에서 중요한 것 두가지만 올려 드리므로 필요하신 분께선 찾아 보십시오.
1. National Oceanic and Atmospheric Administration (NOAA, U.S.A.) :
“A Brief Explanation of the Basic Astronomocal Factors Which Produce
Tides and Tidal Currents”
2. Naval Postgraduate School (NPS, U.S.A.) :
“Navy Operational Ocean Circulation and Tide Models”
(2) 기조력 접근방법론
1. 용어 정리
우선 용어부터 정리해본다. <조석력> 을 말 그대로 풀어쓰면 “밀물, 썰물의 힘” 이고, <기조력>은 “밀물, 썰물을 일으키는 힘” 이다. 조석력은 한자로 潮汐力 이라 쓰고, 기조력은 起潮力 이다.
“아침 저녁”의 <조석> 은 朝夕 이라한다. <潮> 는 아침에 일어나는 밀물 또는 썰물을 말하며
<汐> 은 저녁 때 일어나는 밀물, 썰물이다. 다만 <기조력>은 오직 아침에 일어나는 밀물 또는 썰물을 일으키는 힘을 뜻하지는 않고, <기조석력> 의 줄인 말일 것이다. 한편 영어로 조석력은 <Tidal Force> 이고, 기조력을 풀어 쓴다면 <Tide Generating Force> 가 될 것이다. 이 칼럼에서는 우리말로는 <기조력> 이란 단어를 쓰고, 영어를 써야할 경우는 <Tidal Force> 로 사용하겠다.
그런데 만조 (滿潮), 간조 (干潮) 같은 용어도 기억하실 것이다. 어차피 이 글에 후반부에 나올 단어들이므로 조석과 관련된 주요 단어들을 미리 정리해본다. 기타 용어는 이 글 맨 후반부 “인천 앞바다 조석시간표” 부분에서 추가로 다루겠다.
1. 밀물 (Flowing Tide, Rising Tide) : 바닷물이 육지 쪽으로 몰려 가는 현상.
2. 썰물 (Falling Tide, Ebbing Tide) : 바닷물이 바다 쪽으로 몰려 가는 현상.
3. 만조 (High Tide) : 밀물이 끝나고 바닷물이 가장 많이 들어온 상태.
4. 간조 (Low Tide) : 썰물이 끝나고 바닷물이 가장 많이 빠져나간 상태.
5. 사리 (Spring Tide) : 만조, 간조 수위차가 큰 시기. 음력 15일, 30일.
6. 조금 (Neap Tide) : 만조, 간조 수위차가 작은 시기. 음력 8일, 23일.
저는 예전에 조석력 같이 지구 바다에서 일어나는 현상을 설명하는 단어들이 천체물리학에서도 사용되는 것을 보고 희한하게 생각되기도 했다. 생각건대 아마도 지구에서 일어나는 밀물, 썰물을 일으키는 힘을 연구하다보니 우주 전체에 적용되는 힘이란 것을 알게 되었는데 그 이후 다른 적당한 용어가 생각나지 않아 그대로 사용되지 않았을까 추정해 본다.
2. 원심력+중력과 중력차이
달의 위치 변화와 밀물, 썰물이 관련 있다는 것은 그리이스 시대부터 내려오는 지식이었으나, 실제로 밀물, 썰물 현상에 대해 과학적으로 처음 설명된 책은 1687년 Issac Newton (1643~1727) 의 Principia 가 처음이다. Newton 은 기조력이 달, 지구, 태양 세가지 천체의 상호 인력작용으로 생기는 현상으로 설명했는데, 지구 전체가 같은 수심의 바다로 완전히 덮여 있는 것으로 가정하고 논리가 전개되어 있다고 한다. 이 같은 가정으로 전개되는 조석이론을 Equilibrium Theory (평형이론) 이라 한다.
그 후 약 100년 후에 Pierre-Simon, Marquis de Laplace (라플라스, 1749~1827) 등 여러 학자들은 수심차이, 해수운동 등을 고려해서 조석운동을 설명하는 방적식을 개발했는데 이를 Dynamic Theory (동적이론) 으로 부른다. 하여간 Newton 으로 인해 <지구 바다> 에서 밀물, 썰물이 생기는 힘인 기조력이 드디어 <천체물리학> 영역으로 진입하게 되었고 그것도 달, 지구, 태양이 관련된 골 아픈 <삼체문제 (Three-Body Problem)> 가 된 것이다.
지구 바다에서의 기조력만을 살펴보려면 세 천체의 질량, 중력 뿐만 아니라 각 천체의 공전, 자전, 상대적 위치 등 고려해야 할 변수가 너무 많다. 그 중에서 달이 지구의 질량중심 (Barycenter) 을 공전하면서 발생되는 지구의 미세한 요동에 따른 <원심력 (Centrifugal Force)> 과 <달과 태양의 중력> 을 변수로 설명하는 방식이 있는데, 이는 주로 해양학 (Oceanography) 에서 사용된다.
이는 공전 (Revolution) 운동하는 물체의 기조력을 설명하기에 적합하다. 위에 언급드린 원심력은 지구의 자전이나 공전으로 인한 원심력이 아니고 <달의 지구 공전으로 인해 지구 표면에서 발생되는 원심력> 이다. 후반부에서 다시 자세히 설명 드리겠다.
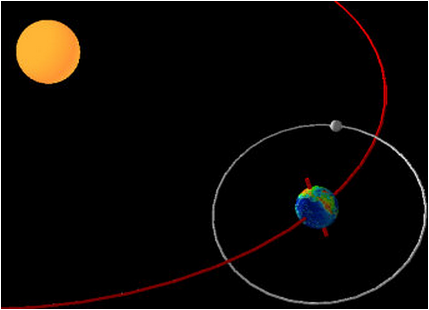
<공전운동하는 천체간의 기조력. 그림 library.thinkquest.org>
그러나 시야를 넓혀 Shoemaker-Levy 9 혜성 같이 공전운동 없이 목성으로 돌진하는 물체에 작용하는 기조력을 설명할 때는 <중력차이> 로만 설명하는 것이 더 간단하고 이해하기 쉽다. 여기서 중력차이란 두 천체 사이의 중력에 차이가 생긴다는 말이 아니고, <A 천체가 B 라는 상대방 천체에 중력영향을 미칠 때, B 천체의 표면 위치에 따라 A 천체가 미치는 중력의 크기가 모두 다른 것>을 의미한다. 물론 어떤 천체에 다른 천체가 접근할 때는 모두 타원 같은 곡선이 되지만, 여기서는 공전운동 (Revolution) 은 하지 않을 때를 말한다.

<목성으로 돌진하는 Shoemaker-Levy 9 혜성의 기조력.
그림 commons.wikimedia.org>
저는 Newton 의 Principia 원본을 읽어 보지 못해 거기서 기조력을 어떤 방법으로 설명하는지 알지 못하지만 아마도 중력차이로 설명하지 않을까 추정한다. 요즘 해양학에서는 주로 첫번째 방법이 사용되며, 두번째 방법은 천체물리학에서 사용되는 것으로 생각된다. 물론 “주로” 사용된다는 것이며 경우에 따라 적절한 방법을 택하면 될 것이다. 비록 설명 방법은 다르더라도 물리적으로 두 힘은 당연히 같을 것이다. 간단히 정리 드리면 아래와 같다.
관련분야 고려하는 변수 적절한 경우
-----------------------------------------------------------------------------------------
해양학 지구표면 원심력 + 달의 중력 공전운동하는 천체
천체물리학 천체 표면위치에 따른 중력차이 공전없이 접근하는 천체
------------------------------------------------------------------------------------------
(3) 중력차이 이론
아래에선 비교적 이해하기 쉬운 중력차이 이론을 먼저 설명 드리고 원심력+중력 이론은 그 아래에서 살펴보겠다.
1. 지구표면 각 지점에 작용하는 중력차이
본 칼럼에서 몇번 언급드렸던 중력 (만유인력) 의 정의는 아래와 같다.
중력 (Fg) Fg = G m1 m2 / r ²
- G : 중력상수 (Serial No 10 참조)
6.67384 x 10−11 N m2 / kg 2 또는
6.67384 x 10−11 m3 kg -1 sec -2 오차범위 1.2 x 10−4
- m1, m2 : 두가지 물체 각각의 질량
- r : m1 과 m2 사이의 거리
따라서 두 물체가 가까이 있으면 그 거리의 제곱 만큼 더 큰 중력을 받게된다. 이는 상대편 천체 표면에서의 위치에도 적용되는데, 상대편 천체와 <마주 보고 가까이> 있는 곳은 상대편 천체<뒷편에 있는 곳> 보다 더 큰 중력 (만유인력) 을 받을 것이다. 이를 태양은 제외하고 지구와 달의 경우만 생각해보면 아래와 같다.
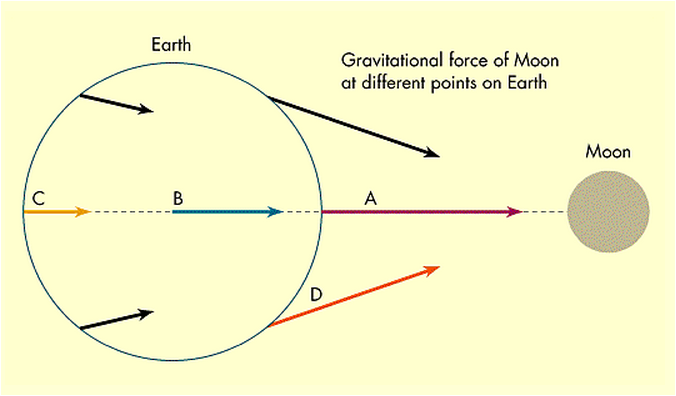
<지구표면 각 지점에서 받는 달의 중력. 그림 exoplanet.as.arizona.edu>
위 그림에서 A,B,C,D 는 지구의 각 지점에서 받는 달의 중력의 크기를 표현한 그림이다.
중력 공식 Fg = G m1 m2 / r ² 에서 보시듯이 상대편 천체와 마주 보고 가까이 있는 A 지점은 뒷편에 있는 C 지점과 비교해서 달과의 거리차이의 제곱 만큼 더 큰 중력을 받을 것이다. 한편 중력의 방향은 달의 중심으로 집중될 것이므로 그림에서 화살표로 표시했다. <중력> 의 크기와 방향은 위와 같을 것이라고 쉽게 이해된다. 그러면 무엇을 <기조력>이라고 부르는 것인가 ?
위 그림에서 지구가 질량이 극히 작은 돌덩이라고 가정하고 달이 FgA 만큼의 중력 (인력) 으로 끌어 당긴다면, A 지점 (Point) 은 당연히 FgA 크기 만큼 오른쪽으로 이동할 것이다. 그러나 현실적으론 A 지점은 지구의 일부이며 지구자체의 질량이 뒤에서 받치고 있어 실제론 FgA 크기 만큼 멀리 이동하지는 못할 것이다.
이를 물리적으로 표현한다면 A 지점은 <지구중심과 달사이의 중력> 으로 인해 <뒤로 당겨지는 것과 같은 효과> 를 보일 것이다. 여기서 지구중심과 달사이의 중력은 <지구 중심인 B 지점이 받는 달의 중력> 이 될 것이고 뒤로 당겨지는 것과 같은 효과란 B 지점의 중력의 <마이너스 ( - ) 효과> 일 것이며, 마이너스 ( - ) 효과란 그 만큼을 뺀다는 의미이다. 여기서 <A 지점이 실제로 당겨지는 힘> 을 A 지점의 <기조력> 이라고 한다.
요약하면 A 지점의 기조력은
<A 지점이 받는 달의 중력과
지구중심인 B 지점이 받는 달의 중력의 마이너스 ( - ) 효과를 합계> 한 것이다.
이를 쉽게 표현하면
<A 지점이 받는 달의 중력에서
지구중심인 B 지점이 받는 달의 중력을 뺀 것> 이 되며,
수식으로 표시하면
FtA = FgA – FgB FtA : A 지점의 기조력
FgA : A 지점이 받는 달의 중력 (다음부터는 A 로 표시함)
FgB : B 지점이 받는 달의 중력 (다음부터는 B 로 표시함)
가 될 것이다.
아래 그림은 A,B,C,D 각 지점의 기조력을 크기 뿐 아니라 방향까지 표시한 것이다. 그림이 복잡해 보이지만 별 것 아니므로 천천히 보시기 바랍니다.
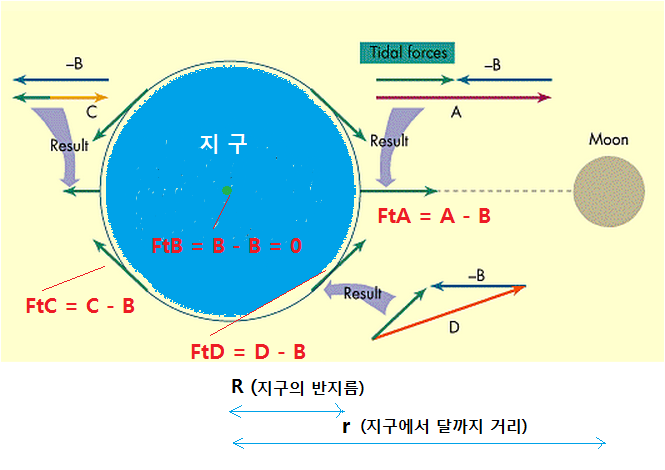
<달의 중력으로 인한 지구표면 각 지점의 기조력.
exoplanet.as.arizona.edu 그림에 일부 추가>
그림에서 기호 의미는 아래와 같다. 또한 지구와 달의 질량도 기호화 한다.
1. A, B, C, D : A, B, C, D 지점에 작용하는 달의 중력
2. FtA, FtB, FtC, FtD : A, B, C, D 지점에 작용하는 달의 기조력
3. r : 지구중심에서 달 중심까지 거리
4. R : 지구 반지름
5. Me : 지구 질량
6. Mm : 달 질량
위 그림에서 A, B, C, D 지점에 작용하는 달의 기조력을 설명드리면 아래와 같다.
A 지점 기조력 : FtA = A – B (FtA = FgA – FgB 를 단순화 한 것)
A 지점 중력에서 지구 중심 B 지점 중력의 <차이>이다.
방향은 달 방향 ( + 방향)
B 지점 기조력 : FtB = B – B
B 지점 중력에서 같은 힘을 빼므로 ( 0 ) 이 된다.
따라서 움직임은 없다.
C 지점 기조력 : FtC = C – B
C 지점 중력에서 지구 중심 B 지점 중력의 <차이>.
C 크기가 B 보다 작으므로 수치는 ( - ) 이다.
이는 방향이 달 반대방향임을 나타낸다.
D 지점 기조력 : FtD = D – B
D 지점 중력에서 지구 중심 B 지점 중력의 <차이>.
벡터 D 에서 벡터 B 를 뺀 값이므로 기조력은 그림의 화살표 방향이다.
위 설명을 지구 전체에 적용해서 기조력 크기와 방향을 표시하면 아래와 같이 될 것이다.
다만 지구가 달을 마주보고 있는 쪽의 기조력의 그 반대편 보다 다소 크다고 알고계시면 된다.
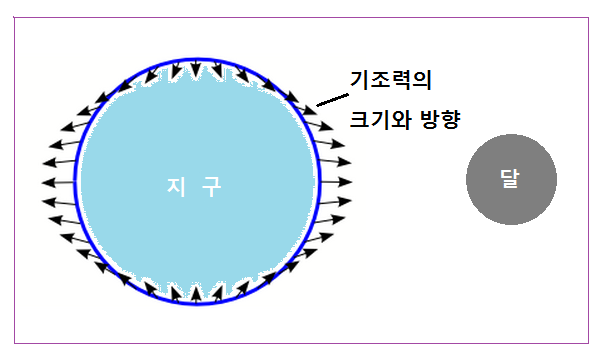
<지구 표면 전체의 기조력 크기와 방향>
2. 기조력 크기 수치화
그러면 A 지점과 C 지점 두 곳의 기조력 크기를 구해 보겠다.
바로 위 두번째 그림 <달의 중력으로 인한 지구표면 각 지점의 기조력> 을 보시면 기호 의미를 더 쉽게 이해하실 수 있다.
A, B, C 각 지점에서 달의 중력은
A = G Me Mm / (r – R) ²
B = G Me Mm / r ²
C = G Me Mm / (r + R) ²
A 지점에서 달의 기조력은
FtA = A – B
따라서
FtA = A – B
= {G Me Mm / (r – R) ² } – {G Me Mm / r ² }
분모를 통분한 다음, R 은 r 보다 매우 작은 것을 고려해서
R/r = 0 및 r – R = r 로 가정하고 위식을 정리하면,
FtA = G Me Mm 2 R / r ³ 이 된다.
따라서 기조력은
1. 두 물체 질량, 해당 물체 지름에 비례하고,
2. 두 지점 사이 거리의 세제곱에 반비례 한다.
또한 FtC 도 구해보면
FtC = C – B
= {G Me Mm / (r + R) ²} – {G Me Mm / r ²}
분모를 통분한 다음, R 은 r 보다 매우 작은 것을 고려해서
R/r = 0 및 r + R = r 로 가정하고 위식을 정리하면,
FtC = 마이너스 G Me Mm 2 R / (r + R) ³ 이 된다.
1. 마이너스 ( - ) 값은 기조력이 달 반대방향임을 나타낸다.
2. 또한 FtA 는 분모가 r ³ 이었는데, FtC 의 분모는 (r + R) ³ 이므로
FtA 가 FrC 보다 절대값이 조금 크다는 것을 알 수 있다.
이는 상대 천체를 마주보는 A 지점의 기조력이 반대편 C 지점보다 조금 크다는 의미이다.
위의 그림에서 지구가 달을 마주보는 지점 A 의 기조력이 반대편 지점 C 보다 조금 크기
때문에 밀물도 더 높이 올라간다.
이 <중력차이론> 으로는 유체인 지구 바다의 조석현상 뿐만 아니라 Shoemaker-Levy 9 혜성 같이 암석으로 이루어진 천체가 목성에 접근하면서 목성의 강력한 기조력 때문에 찌그러지다가 일정한계를 지나면 결국 여러 조각으로 깨지는 현상을 쉽게 설명할 수 있다. 이 같이 물체가 깨지기 시작하는 거리를 <로쉬의 한계, Roche’s Limit> 라고 하는데, 바로 다음 <Not Essential But Beneficial> 칼럼에서 다시 언급드린다.
(4) 원심력+중력 이론
1. 지구표면 각 지점에서 달이 지구에 미치는 중력 차이
중력차이론은 우주천체 상호간 기조력에 적용하기 쉽지만 지구바다의 조석현상은 이미 언급드린대로 고려해야할 변수가 너무 많다. 아래에선 주로 지구 해양학에서 사용되는 <원심력+중력론> 살펴보겠다. 지구바다의 조석현상에 대한 것이므로 달과 태양을 주요 변수로 취급한다. 여기서는 간단한 논의를 위해 <달> 중력 위주로 설명 드린다. 태양의 중력은 달과 같은 원리로 생각하시면 되고, 태양-달-지구의 위치에 따른 중력 변동만 고려하시면 될 것이다.
우선 위의 첫번째 그림에서 지구-달 관계에서 지구표면 각 지점에 작용하는 중력은 A, B, C 등이며 지구표면 각 지점에서 달이 지구에 미치는 중력에 차이가 있다는 점을 생각하시면 된다.
2. 지구표면 각 지점에서 생기는 원심력
a) 지구자체 중심과 지구-달 질량중심의 운동궤적
지구 표면에 발생되는 원심력 (Centrifugal Force) 에 대해선 생소한 분이 많으실 것이다. 대부분의 일반 과학 서적들이 달의 지구 공전을 설명할 때 <지구의 중심>을 도는 것처럼 설명하기 때문이다. 그러나 Seral No 12 에서 설명 드린 것처럼 우주의 모든 천체들이 상호 공전할 때는 상대방 천체의 중심을 공전하는 것이 아니고 <질량중심 (Center of Mass 또는 Barycenter)> 을 축으로 공전한다. 다중성인 경우도 여러 천체의 질량 중심을 공전한다. 경우에 따라 질량중심이 천체 바깥의 특정 공간에 존재하는 경우도 있다. 상세한 사항은 Serial No 12 를 보시기 바란다.
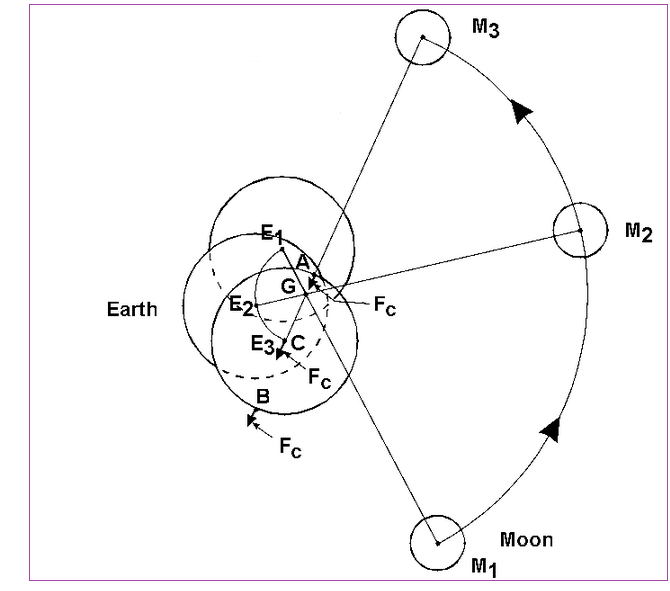
<지구와의 상호 질량중심을 축으로 공전하는 달. 그림 NOAA>
위의 그림은 달이 지구 중심을 축으로 공전하는 것이 아니고 지구와의 상호 질량중심을 축으로 공전하는 모습을 표현한 것이다. 달이 M1 à M2 à M3 위치로 지구를 공전할 때 지구의 각 지점 위치는 아래와 같다. 참고로 아래에서 다시 설명 드리겠으나, Fc 는 달이 M3 위치에 있을 때 지구 표면 각 부분에 작용하는 원심력이며, 이 힘의 크기는 지구 표면 어디서나 같은 크기의 힘이다.
달 위치 지구중심 달-지구 상호 질량중심 원심력
--------------------------------------------------------------------------------------------
M 1 E 1 G (위치고정) Fc (지구 표면 어디서나 같은 크기)
M 2 E 2 G (위치고정) Fc (지구 표면 어디서나 같은 크기)
M 3 E 3 G (위치고정) Fc (지구 표면 어디서나 같은 크기)
---------------------------------------------------------------------------------------------
그림 내용을 다시 정리하면 아래와 같다.
1. 달의 지구공전 위치변화에 따라 지구 중심 위치 (E)도 같이 변한다.
2. 지구 중심 (E) 는 달의 지구공전에 따라 원 운동 한다.
지구 중심의 원운동에 대한 추가 설명은 바로 아래를 보시면 됩니다.
3. 달이 지구를 공전해도 달-지구 상호 질량중심 위치 (G) 는 변하지 않는다.
4. 지구 표면 각 부분에 작용하는 원심력 (Fc) 는 지구 표면 어디서나 같은 크기의 힘이다.
원심력 부분은 아래에서 다시 자세히 언급 드립니다.
위의 정지상태 그림으로는 이해 어려우신 분들이 많으실 것이다. 원치복 서울지부장님께서 동영상을 보내 주셨는데 여기서는 해당 동영상 캡처한 그림 4개만 올려 드린다. 그림에서 흰색 십자선은 <지구-달 공전궤도의 질량중심> 이고, 붉은 색 점은 제가 별도로 표시한 <지구자체의 중심 (질량중심)> 이다. 달이 지구를 공전함에 따라 흰색 십자선은 공전궤도의 중심으로 고정되어 있으나 붉은 색 점은 원형궤적으로 운동함을 살펴보시기 바랍니다.
해당 동영상을 <자료실> 이나 <자유게시판>에 올려보려 했는데, avi 파일로 되어서 그런지 업로드가 되지 않았
습니다. 제가 파일변환하는 능력이 없으므로 필요하신 분께서 요청하시면 별도로 보내드리겠습니다.
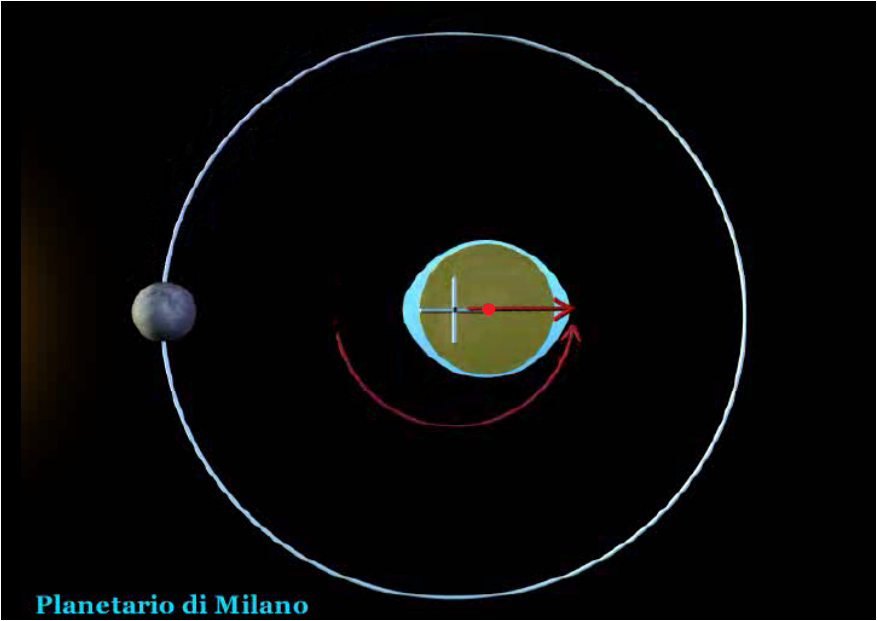
<그림 1 지구자체 중심과 지구-달 공전궤도의 질량중심의 운동. 그림 Planetario di Milano>
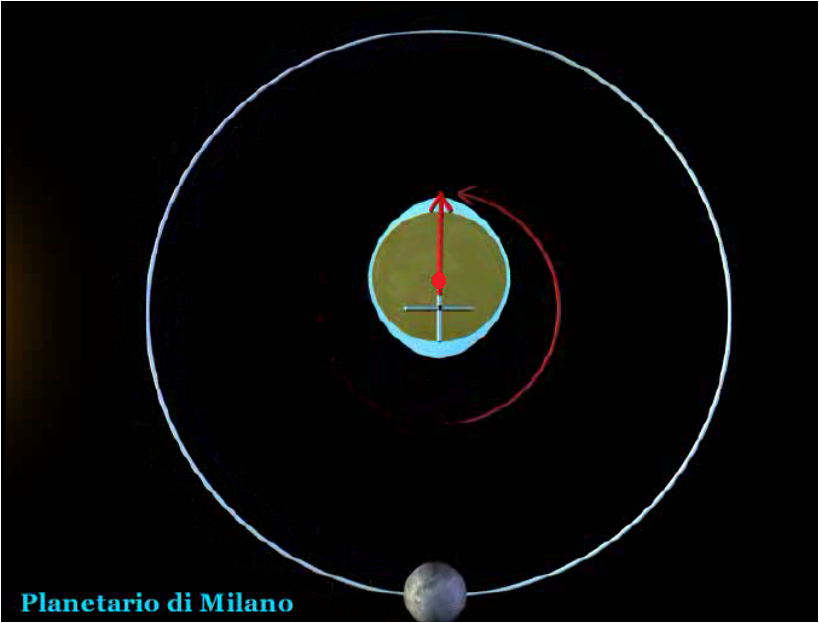
<그림 2 지구자체 중심과 지구-달 공전궤도의 질량중심의 운동. 그림 Planetario di Milano>
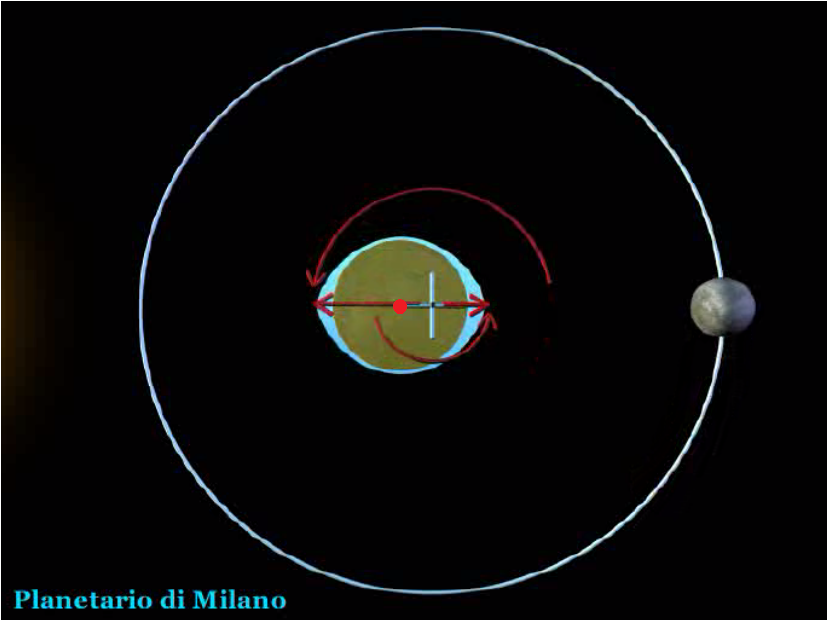
<그림 3 지구자체 중심과 지구-달 공전궤도의 질량중심의 운동. 그림 Planetario di Milano>
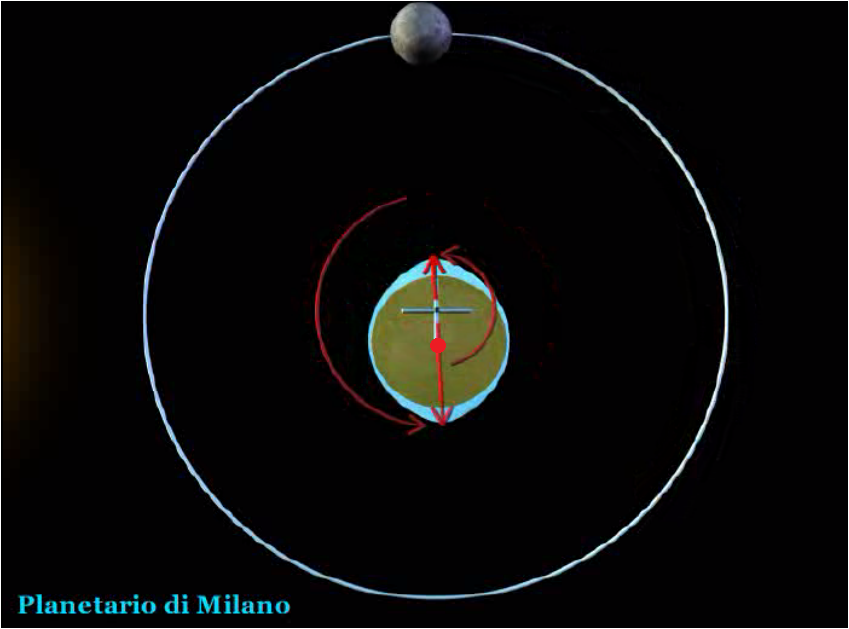
<그림 4 지구자체 중심과 지구-달 공전궤도의 질량중심의 운동. 그림 Planetario di Milano>
위에서 붉은 색 점인 지구자체 중심은 달이 지구를 공전함에 따라 원형궤적으로 운동하는 것을 보셨을 것이다. 지구 위치를 고정시키고 다시 그리면 아래와 같다.
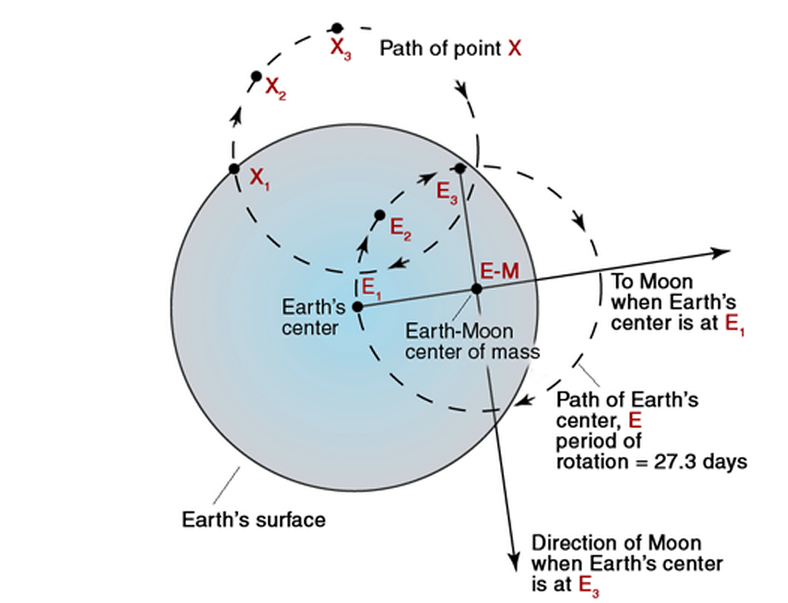
<달의 지구공전에 따른 지구표면 특정 지점의 운동궤적. 그림 NPS >
지구 중심 E 는 달이 지구를 공전함에 따라서 E 1 / E 2 / E3 를 따라 위의 점선처럼 원운동 하게 되며 마찬가지로 지구의 어떤 특정한 지점 X 도 X 1 / X 2 / X 3 의 궤적을 원운동 하게 된다. 지구의 어떤 지점들이 원 운동하는 방향은 <달이 지구를 공전하는 방향과 같은> 방향이다. 동영상 을 캡처한 그림에선 달이 <시계 반대방향> 으로 공전하지만, 바로 위의 정지상태 그림은 동영상 그림과는 다르게, 달이 <시계방향> 으로 공전하는 것으로 그려져 있으므로 혼동 없으시기 바랍니다. 만일 지구의 태양 공전궤도를 과장해서 그리면 아래와 같을 것이다.
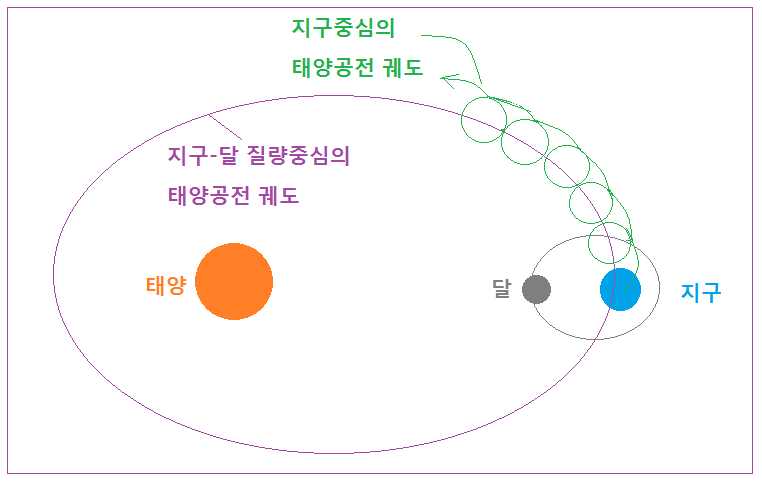
<지구중심과 지구-달 질량중심의 태양 공전궤적>
b) 지구표면 위의 원심력
이처럼 지구 표면 모든 점들은 달이 지구를 공전하는 방향과 같은 방향으로, 지구 중심이 원운동하는 반지름과 동일한 반지름으로 원운동 하게 된다. 그런데 원운동하는 모든 물체에는 원심력과 구심력이 작용함은 잘 아실 것이다. 따라서 지구표면 모든 위치에도 원심력과 구심력이 작용할텐데, 이 때의 구심력은 달의 인력 (중력) 이 되고 원심력은 달의 반대방향으로 나타날 것이다.
이를 그림으로 그리면 아래와 같다.
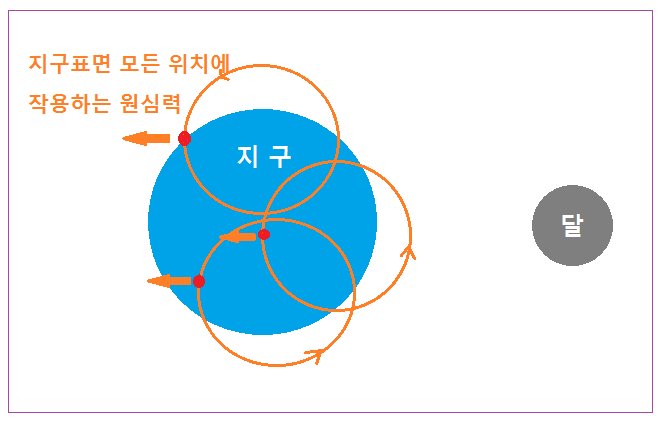
<지구 표면 모든 위치에 작용하는 원심력>
한편 지난호 Serial No 18 에서 언급드린 원운동하는 물체의 원심력은 아래와 같다.
원심력 (Fc) Fc=m r ω2 - m : 물체의 질량.
- r : 물체가 원운동 할 때 반지름
- ω : 물체가 원운동 할 때 각속도
여기서 바다 <물 분자> 각각을 생각해보면, 물 분자 한 개의 질량은 모두 같다고 가정한다면, 원운동 반지름도 같고, 각속도도 지구표면의 모든 위치에서 동일하므로 원심력 크기 또한 모두 같을 것이다.
3. 지구표면 위의 원심력과 달의 인력의 합계
한편 위의 “지구표면 각 지점에 작용하는 중력차이” 항목에서 설명 드린 것처럼, 상대편 천체와 마주 보고 가까이 있는 곳은 상대편 천체 뒷편에 있는 곳보다 더 큰 중력 (만유인력) 을 받는다. . 따라서 달에 가까운 쪽은 멀리 있는 것보다 상대적으로 곳보다 더 큰 중력을 받을 것이다. 여기서 기조력은 <지구 어디서나 동일한 “원심력” 과 지구 상 위치에 따라 다른 “달의 중력 (인력)” 의 합계”> 로 정의된다. 이를 그림으로 나타내면 아래와 같다.
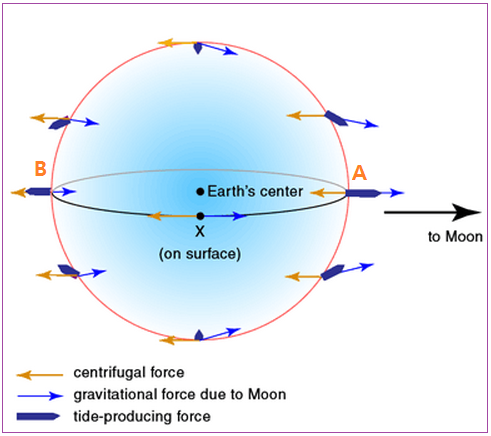
<기조력 = 원심력 + 달의 인력 (중력). NPS 그림에 일부 추가.
노란 화살표 : 원심력. 파란 화살표 : 달의 인력. 두꺼운 파란 화살표 : 기조력>
위에서 A 지점에선 (인력 > 원심력) 이고 B 지점에선 (인력 < 원심력) 이다. 따라서 그 두 힘의 합계인 기조력은 두꺼운 파란 화살표로 나타나며, A 지점의 인력이 B 지점의 인력보다 크므로 기조력도 A 지점이 B 지점보다 더 크다. 위의 <중력차이 이론> 에서 올려드린 <기조력 크기와 방향> 그림을 참조하시기 바랍니다.
(5) 태양의 기조력과 달의 기조력 차이는 얼마나 될까 ?
위에선 달이 지구에 미치는 기조력만으로 설명 드렸다. 그러나 이미 밀씀드린대로 태양의 기조력을 무시할 수는 없을 것이다. 참고 삼아 태양이 지구에 미치는 기조력은 달이 지구에 미치는 기조력과 비교해서 얼마나 되는지 계산해본다. 두 천체의 기조력만 비교하는 것이므로 지구표면 A 지점에 미치는 기조력으로만 가정한다. 다만 거리는 각 천체 중심사이의 거리로 계산한다.
우선 위의 <중력차이론>에서 계산한 기조력은 아래와 같다.
FtA = G Me Mm 2 R / r ³ - G : 중력상수
- Me : 지구 질량
- Mm : 달 질량
- r : 지구중심에서 달 중심까지 거리
- R : 지구 반지름
위의 식에서 G, Me, R 은 상수이다. 나머지 Mm 과 r 이 변수인데, 이는 상대천체의 질량과 거리이다. 따라서 기조력은 아래와 같이 말할 수 있다.
기조력은 상대 천체의 질량에 비례 하고 거리의 세제곱에 반비례 한다.
우선 필요한 수치는 아래와 같다.
Me : 지구 질량 (kg) = 6.0 x 10의 24승수 kg
Ms : 태양 질량 (kg) = 2.0 x 10의 30승수 kg
Mm : 달 질량 (kg) = 7.4 x 10의 22승수 kg
Rs : 지구에서 태양까지 거리 (km) = 1.5 x 10의 8승수 km
Rm : 지구에서 달까지 거리 (km) = 38.5 x 10의 4승수 km
여기선 기조력의 <절대값>을 구하는 것이 아니고 단지 <배수> 만 비교하는 것이므로
지구질량과 지구-달 거리를 1 로 가정하고 태양과의 배수를 계산한다.
지구-태양 거리 / 지구-달 거리 = 1.5 x 10의 8승수 / 38.5 x 10의 4승수
= 389.61 배
태양 질량 / 지구 질량 = 2.0 x 10의 30승수 / 6.0 x 10의 24승수
= 333,333 배
지구 질량 / 달 질량 = 6.0 x 10의 24승수 / 7.4 x 10의 22승수
= 0.0123 배
태양 기조력이 달 기조력의 몇 배인지 계산하면,
333,333 0.0123
------------ ÷ ----------- = 0.4582 가 된다.
(389.61) ³ 1 ³
따라서 태양 기조력은 달 기조력의 0.4582 배, 또는 45.82 % 가 된다.
수치를 정확히 해서 계산하면 위의 수치가 43 % 정도 된다고 한다.
태양이 멀리 있으나 워낙 크므로 달보다는 조석력이 클 줄 예상했는데, 막상 계산해보니 거리의 세제곱에 반비례하므로 그 힘이 급격히 줄어들어 달의 반 정도 밖에 되지 않음을 알 수 있다.
한편 내행성인 수성 및 금성도 지구의 기조력에 영향을 미칠 것이지만 정도가 극히 미약하므로 일반적으로 조석변화 요인으로는 넣지 않는다. 참고로 금성의 지구에 대한 기조력 영향력은 달의 0.000052 배 (0.0052 %) 라고 한다.
(6) 조석변화에 영향을 주는 천문학적 요인들
1. 달의 위상 변화 (Lunar Phase Effect)
지구의 밀물 및 썰물은 지구상 위치에 따라 그 높이도 다르고 발생하는 시간도 계절에 따라 조금씩 차이가 난다. 또한 어떤 지역은 하루에 두번 밀물, 썰물이 생기지만 어떤 지역은 하루에 한번만 일어난다. 여기서는 지리적 상황은 제외학고 오직 천문학 분야에 국한해서 그 원인을 살펴보겠다.
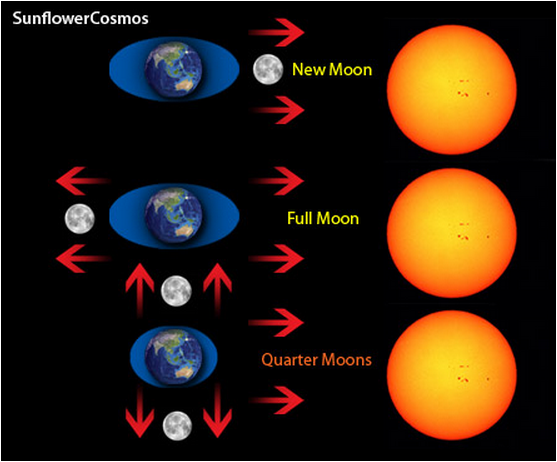
<New Moon: 삭 (그믐), Full Moon : 망 (보름), Quarter Moons (상현 및 하현)
참고로 1st Quarter Moon은 상현, 3rd Quarter Moon 은 하현. 그림 sunflowercosmos.org>
위 그림은 달이 지구를 공전함에 따라 태양-지구-달 위치 변화에 따라 지구에 미치는 기조력차이로 인해 밀물의 높이가 달라짐을 표시한다. 삭 (朔, 그믐)과 망 (望, 보름) 일 때는 태양의 기조력 (달의 43 %) 가 합해져서 가장 높은 밀물이 만들어지며, 밀물과 썰물의 높이 차이도 최대가 된다.
이 때를 <사리 (Spring Tide)> 라고 하며 태양과 달의 위치는 “일직선 위치 (Syzygy) ” 이다.
반대로 상현 및 하현에는 태양 기조력의 방해로 인해 낮은 밀물이 형성 됨을 나타내며, 밀물과 썰물의 높이 차이는 최소가 된다. 이 때를 <조금 (Neap Tide) >라고 하고 태양과 달의 위치는 “직각위치 (Quadrature)” 가 된다. 정리하면 아래와 같다.
태양-달 위치 조석 명칭 밀물과 썰물 지구에서 보이는 달 위상
높이 차이
------------------------------------------------------------------------------------------------
일직선 위치 (Syzygy) 사리 (Spring Tide) 최대 삭 또는 망
직각위치 (Quadrature) 조금 (Neap Tide) 최소 상현 또는 하현
--------------------------------------------------------------------------------------------------
한편 사리나 조금이 반드시 삭망이나 상현, 하현에 일어나지는 않고 2~3 일 차이가 생기는데, 이 글 맨 아래의 “인천 조석시간표” 에서 확인하시면 된다. 그 이유는 바닷물의 해저지형과의 마찰력 및 바닷물의 관성력 방해 등 때문이라고 한다. 달의 삭망월이 약 29.5 일 이므로 <사리 à 다음 사리> 또는 <조금 à 다음 조금> 은 약 15일 주기로 반복된다.
2. 공전궤도상 거리 (Orbital Distance Effect)
모든 천체의 공전궤도는 타원이며, 태양-지구-달은 각각의 궤도 위치에 따라 근일점, 원일점, 근지점, 원지점 등의 구분이 있다. 기조력은 상대 천체와의 거리의 세제곱에 반비례하므로 공전궤도상 위치에 따라 기조력 크기도 변할 것이다. 아래 그림으로 표시해 보았다.
참고로 근일점은 매년 1월초이고, 원일점은 매년 7월초이다. 금년 2013년의 근일점은 우리나라 시간으로 1월 2일 오후 2시 정각 (14:00) 이었고, 원일점은 7월 6일 토요일 0시 0 분이다. (금요일 자정)
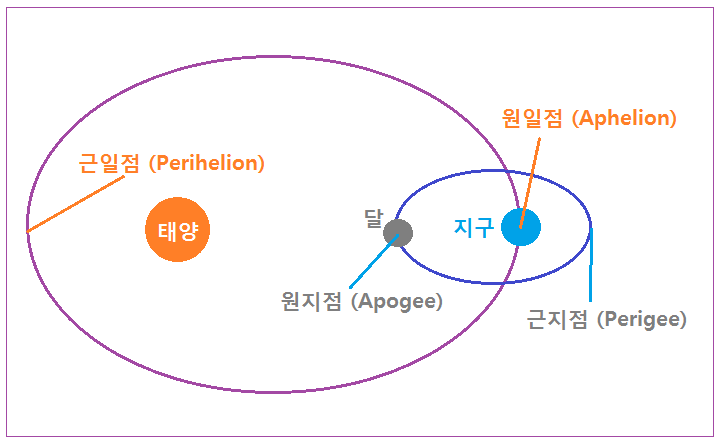
<공전궤도상 거리>
3. 달 공전궤도 기울기 (Lunar Declination Effect)
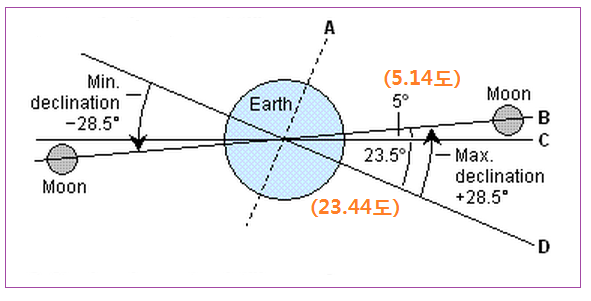
<달의 공전궤도 기울기.
A 지구 자전축, B 달의 지구 공전궤도 면
C 지구의 태양 공전궤도 면, D 지구 적도면>
지구 자전축은 지구의 태양 공전궤도면에 대해 23.44° (약 23.5 °) 기울어져 있고, 이로 인해 지구 중위도 지방에선 4 계절이 생긴다. 그런데 달의 공전궤도면 또한 지구의 공전궤도면에 대해 5.14 ° (약 5 °) 기울어져 있고, 이로 인해 매년 개기일식이 일어나지는 않는다.
따라서 달은 지구의 태양 공전궤도면에 대해 최대 28.58 ° (약 28.5 °) 기울어져 있게 되며 태양-지구-달의 위치에 따라 지구 적도면에 대해 최대 ( + ) 28.58 ° 최소 ( - ) 28.58 ° 가 기울어져 있다. 이로 인해 지구 각 지역에 따라 밀물의 높이 및 밀물, 썰물 주기에 차이가 나게 된다. 우선 아래 그림 보시지요.
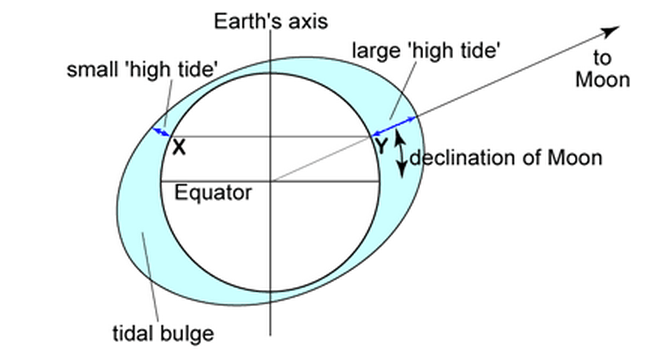
<달의 공전궤도 기울기와 조석차이. 그림 NPS>
위의 그림 지구적도를 수평으로 만든 그림이다. 그림 오른쪽 Declination of the Moon 의 최대 각도는 + 28.58 ° 가 될 것이다. 그림과 같은 경우에는 북위 + 28.58 ° 에서 최대 밀물 높이가 발생하고 남위 - 28.58 ° 에서 북반구보다 조금 작은 높이로 밀물이 일어날 것이다. 이후 달이 그림의 뒤쪽으로 가서 지구 적도와 평행해지면 지구 적도 부근에서 최대 밀물 높이가 일어날 것이다.
밀물의 높이 변화 및 밀물, 썰물 주기에 대한 자세한 사항은 저도 이해가 어려워 추가 설명은 생략한다. 다만 달의 공전궤도 기울기로 인해 지역에 따라 나타나는 일정한 패턴 3개를 아래에 정리해 드린다.
a) Semidiurnal Tide
우리말로는 <반일주 조석> 이 된다.
하루평균 밀물 2회 썰물 2회가 일어나며 밀물, 썰물시 해수면도 각각 비슷한 경우이다.
여기서의 하루는 정확한 24시간이 아니며, 아래에서 다시 설명 드린다.
우리나라 조석이 이에 해당한다.
Tidal Day : 조석일
Tidal Period : 조석주기
Datum : 조석기준면. 이것은 반드시 평균해수면 (Mean Sea level) 과 일치하는 것은
아니다. 우리나라는 <국립해양조사원>에서 지역에 따라 별도로 정한다.
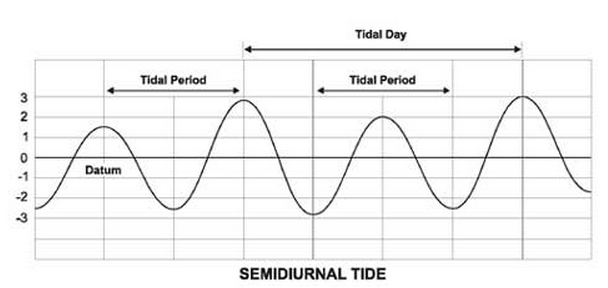
<반일주 조석 그림 NPS>
b) Mixed Tide
우리말로는 <혼합 조석> 정도가 된다.
하루 평균 밀물 2회 썰물 2회가 일어나지만 밀물, 썰물시 해수면에 상당한 차이를
보이는 경우이다. .
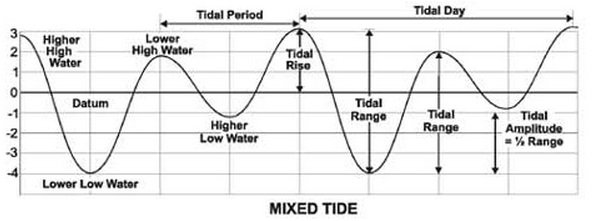
<혼합조석 그림 NPS>
c) Diurnal Tide
우리말로는 <일주 조석> 정도가 된다.
하루평균 밀물 1회, 썰물 1회가 일어나며 밀물, 썰물시 해수면도 각각 비슷한 경우이다.
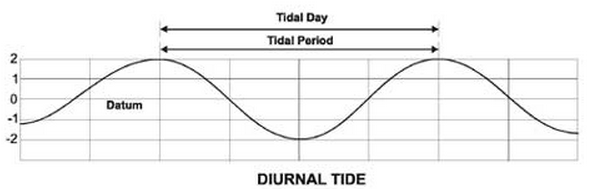
<일주조석 그림 NPS>
(7) 밀물, 썰물시간이 매일 조금씩 차이가 나는 이유
1. 달이 고정되어 있을 경우
이 단락 바로 아래에서 살펴 보겠지만, 하루평균 만조 2회 간조 2회가 일어나는경우라도 그 주기는 정확히 24시간이 아니다. 만일 달이 정지해 있고, 지구만 24시간에 1회 자전한다면 6시간마다 <밀물à 썰물 à 밀물à 썰물 à 밀물> 이 일어나서 24시간이 1주기가 될 것이다.
참고로 밀물이 하루에 2회씩 일어나는 이유는 달이 반대편에 있을 때도 밀물이 일어나기 때문이다. 달을 고정시키고, 지구의 자전만 생각해보자. 지금 0시 0분에 인천이 달을 마주보고 있다면 밀물이 일어날 것이다. 오전 06:00 엔 지구가 서쪽으로 돌아 달과 90 ° 도 가 되어 썰물이 일어나고, 오전 12:00 에는 인천이 달과 180 ° 도 이지만 위의 기조력 설명처럼 달의 반대편에도 수위가 좀 낮지만 밀물이 일어난다. 오후 6:00 이면 다시 달과 270 ° 가 되어 썰물이며 오후 12:00 에는 밀물이 될 것이다. 정리하면 아래와 같다.
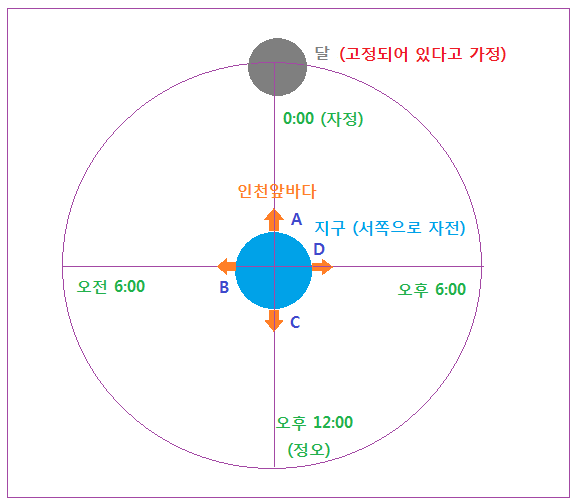
<달이 고정되어 있을 경우의 지구의 밀물과 썰물>
위 그림에서 인천 앞바다가 A 위치에 있을 때 밀물이면 그 때 C 지역 (대척점, Urguay 앞바다) 도 밀물일 것이다. 지구가 자전해서 6시간후 B 위치에 오면 썰물이고, 다시 인천이 C 위치에 오면 밀물이 된다. 이 때 Urguay 앞바다도 밀물이 될 것이다. 요약하면 달이 고정되어 있고 지구만 자전한다면 정확히 6시간마다 밀물, 썰물이 반복된다.
2. 달도 공전운동 할 경우
그런데 문제는 달도 가만있지 못하고 지구를 공전하는데 있다. 달의 지구 공전주기에 대해선 아래의 두개를 생각해 보아야한다.
항성월 (Sidereal Month)
달이 지구를 1 회 공전하는데 걸리는 시간
27.32166 일 (약 27.32일)
삭망월 (Synodic Month)
달 위상이 삭 à 삭 또는 망 à 망이 되는데 걸리는 시간
29.530588 일 (약 29.53 일)
삭망월이 더 긴 이유는 달이 지구를 1바퀴 공전하는 동안 지구도 태양을 공전해서 위치를 바꾸었기 때문에 달이 태양-지구와 다시 일직선이 되려면 지구가 1달 만큼 진행한 공전각도를 따라잡아야 하기 때문이다.
여기서는 지구와 달과의 관계만 생각하므로 항성월을 적용해서 계산한다. 달이 지구를 1회 공전하는 시간은 항성월인 27.32일이다. 달 공전궤도가 원이라 가정하면 달이 지구를 360° 회전하는 데 27.32일이 걸린다는 말이므로 달은 하루 24시간 에 13. 17° 만큼 이동한다.
360 ° ÷ 27.32 일 = 13. 17° / 1일 (24시간)
한편 지구는 하루 24시간에 1회 자전한다.
만일 인천 앞바다가 어느날 자정 0:00 시에 달을 마주보고 있었다면 그 다음날 24시간 이후에 다시 이전의 위치로 돌아와 있을 것이다. 그런데 그 24 시간 동안 달도 지구를 공전해서 13.17 ° 만큼 이동해 있을 것이다. 그림으로 나타내면 아래와 같다
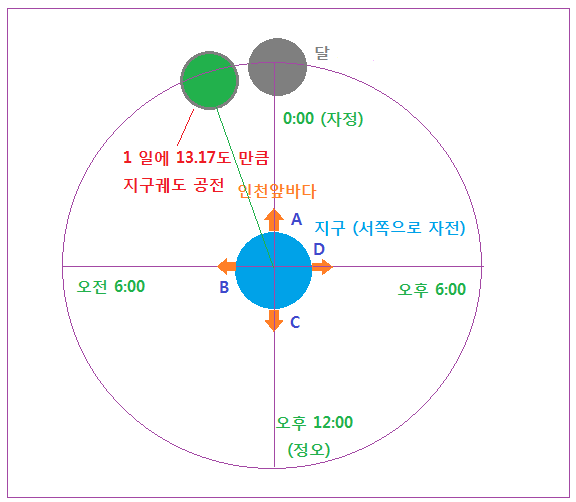
<달이 공전하는 경우의 지구의 밀물과 썰물>
위 그림에서 24 시간 (1일) 동안 달이 움직인 각거리는 13.17 ° 이며 초록색 달로 표시했다.
인천 앞바다가 바로 24시간 전에는 0:00 시 자정에 달을 마주보고 있어 밀물이 일어 났지만 다시 달을 마주보고 밀물이 일어나려면 달이 움직인 각거리인 13.17 ° 만큼 추가로 자전해야 한다.
따라서 지구가 추가로 자전해야 하는 시간은
(13.17 ° x 24 시간) ÷ 360 ° = 0.878 시간
= 52.68 분 (약 50 분)
다시 말하면 <밀물à 썰물 à 밀물à 썰물 à 밀물> 주기는 24시간이 아니고 24시간 + 52.68 분 = 약 24시간 50 분 이 된다. 이를 세분화하면 아래와 같은 주기가 될 것이다.
밀물 à 썰물 à 밀물 à 썰물 à 밀물
6시간 12.5분 6시간 12.5분 6시간 12.5분 6시간 12.5분
12시간 25분 12시간 25분
24시간 50분
(8) 2013년 7월의 인천 앞바다 물때표
그러면 실제로 인천 앞바다 물때표를 보면서 위에서 설명드린 내용이 맞는지 검토해 본다.
참고로 우리나라 <조석예보>는 한국천문연구원이 아니고 <국립해양조사원> 이 담당한다. 영문으로는 Korea Hydrographic and Oceanographic Administration (KHOA) 이다. 아래 물때표는 국립해양조사원 정보를 토대로 Badatime.com 에서 제공한 자료이다.
<인천 앞바다 물때표 (조석간만 시간표)>
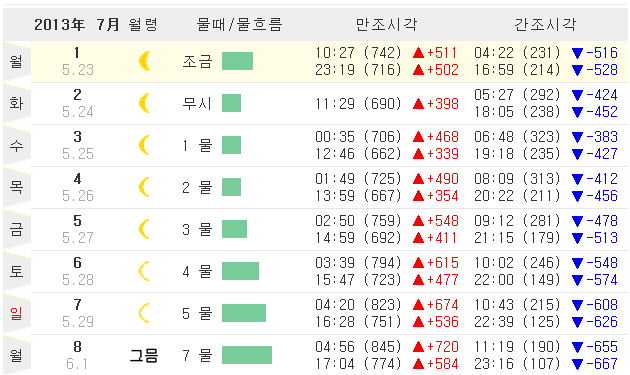

<자료 Badatime.com>
우선 용어 및 물때표 보는 방법부터 정리 드린다. 해당 사이트에 나온 것을 정리한 것이다. 저도 이 칼럼 쓰면서 한 수 배웠고, 앞으로 바다 낚시가면 유용하게 써보아야 겠습니다. 위에서 이미 설명드린 용어는 빼고 새로 나오는 용어만 정리 드린다.
1. 물때표 : 오랜기간 목욕하지 않아서 생기는 것이 아니고, 조석간만 시각을 나타낸 표.
2. 무시 : 조금 다음날. 조금 때와 유사한 수위.
3. 1물, 2물 등 : 조금이나 무시 다음날부터 기산하는 날짜.
관례상 서해는 조금-무시-1물-2물로 기산하고
동해, 남해는 무시는 제외하고 조금- 1물-2물로 기산해 나감.
4. 표에 보이는 숫자의 뜻
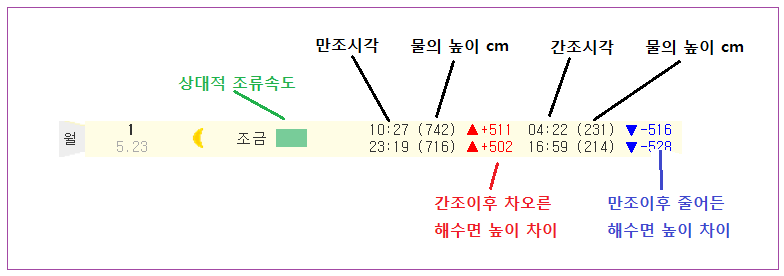
<표에 보이는 숫자의 뜻>
임의로 선정한 날짜인 7월 3일의 물때표를 검토해 보겠다. .
일 자 만조 간조 시각 시간 차이
----------------------------------------------------
7월 3일 만조 00:35
간조 06:48 6 시간 13 분
만조 12:46 5 시간 58 분
간조 19:18 6 시간 32 분
7월 4일 만조 01:49 6시간 31 분
------------------------------------------------------
합 계 25 시간 14 분
위에서 설명드린 주기는 6시간 12.5 분 및 24시간 50분으로 말씀드렸으나 7월 3일의 조석주기는
5시간 58분 ~ 6시간 32분 및 25시간 14 분으로 차이가 많다. 이 같은 차이는 서해의 수심 및 바다의 입구가 닫혀있는 지형 등이 원인이라고 한다.
다음으론 삭 (그믐) 이나 망 (보름) 에서 최고 수위가 되는지 알아본다. 위에서 언급 드린대로 사리나 조금이 삭망이나 상현, 하현에서 생기지는 않고 천문학 외적인 요인으로 며칠 차이가 생기는 것을 알 수 있다. 아래는 “삭 (그믐)” 인 7월 8일 보다 3~4일 늦은 7월 11~12일의 수위가 제일 높은 것을 보여준다.
---------------------------------------------------------------------
그믐 (삭) 7월 8일 8 m 45 cm
7월 1~15일 최고수위 7월 11~12일 8 m 80 cm
---------------------------------------------------------------------
기조력을 알아보려 하다가 인천 앞바다까지 나왔으니 깊이는 없었으나 그래도 주마간산 (走馬看山) 은 되었을 것 같다. 앞으로 해변으로 나가셨을 때 출렁이는 바다를 보시면서 <기조력> 이란 단어를 떠올리시게 된다면 칼럼 쓰는 보람이 될 것이다.
II. Not Essential But Beneficial
Roche’s Limit (로쉬의 한계) – 가까이 오면 다친다 !
(1) It’s non of my business ?
미국인들과 거래하면서 가끔 듣는 말 중에 “It’s non of my business” 라는 말이 있다. 우리말로 “그건 내 알 바 아니야” 라는 뜻인데, 이 말 들을 때마다 정말 그들에게 정 떨어진다. 아마도 건국 초기 이민자들의 험난했던 생활상을 반영한 말이라 생각된다. 영화 <Gangs of New York>을 보면 미국 남북전쟁 (1861~1865) 당시 New York 에 살던 Ireland 이민자들의 살벌한 생활이 잘 나타난다. 20세기 초기 Italy 이민자들의 New York 생활을 보려면 <대부 2 (The Godfather Part II)> 가 제격이고…. 이런 영화 내용처럼 “남들이 죽어나가건 말건, 내게 이익이 되지 않으면 신경 안쓴다는 말을 바꾸어 말한다면, “내게 이익이 된다면 남들을 해칠 수도 있다” 는 말과 다를 바 없다.
제가 이런 좀 거북스러운 말로 칼럼을 시작하는 이유는 “대부분” 사람들이 “아무리 큰 사건이라도 내게서 먼 거리에서 일어나면 중요한 일 아니다” 라고 생각한다는 말씀을 드리려했기 때문이다. “아프리카에서 10억명이 굶어도 내 손톱 밑 가시의 아픔과는 비교도 안된다” 는 말도 생각난다. 물론 “대부분” 사람들이 그렇다는 말이고, 일부 생각 깊으신 분들은 멀리 아프리카 어린이들을 위해 많은 기부를 해오는 것도 보았다. 과연 어떻게 사는 것이 제대로 사는 건지 한 번 생각해 볼 일이다.
하여간 수천, 수억 광년 떨어진 은하들 사이의 기조력 때문에 일어나는 은하들의 충돌이나 뒤틀림은 인천 앞바다 밀물이 어느날 1 미터 더 오르는 것에 비하면 뉴스거리도 아니다. 공룡이 소행성으로 멸종했다는 가설이 힘을 얻어도 대부분 지구인들은 한 평생 “설마 나 또는 내 자식들 세대에 또 그런 일이 생기진 않겠지” 라는 생각으로 살아왔다. 그런데 1994년 7월에 와서 모든 지구인들 정신을 번쩍 들게 만드는 사건이 생기는데, 바로 슈메이커-레비 9 혜성 (Shoemaker-Levy 9) 의 목성충돌이었다.
이 혜성의 한 조각이 목성에 충돌하면서 발생하는 폭발면적이 지구 크기임을 보면서 비로소 지구인들은 “아. 지구도 한 방에 갈 수 있구나” 라는 사실을 실감하게 되었다. 그런데 그 혜성 조각들은 실제로 21 개 였다 ! 스물 한 방의 연타… 21 번에 걸친 지구 멸종…. 이 혜성이 경로를 조금만 바꾸어 지구로 돌진했다면 어찌 되었을지는 모두 별로 생각하고 싶지 않으실 것이다.
(2) 슈메이커-레비 9 혜성의 경우
여기서는 위에서 살펴본 기조력으로 인해서 <천체가 파괴되기 시작하는 거리> 를 알아보려 한다. 그 실제의 예로서 멀리 있는 은하들 보다는 아직도 모든 분들 기억에 생생한 <슈메이커-레비 9 혜성> 을 예를 들어 설명 드리겠다. 우선 이 혜성의 충돌과정을 표현한 그림 먼저 보시지요.
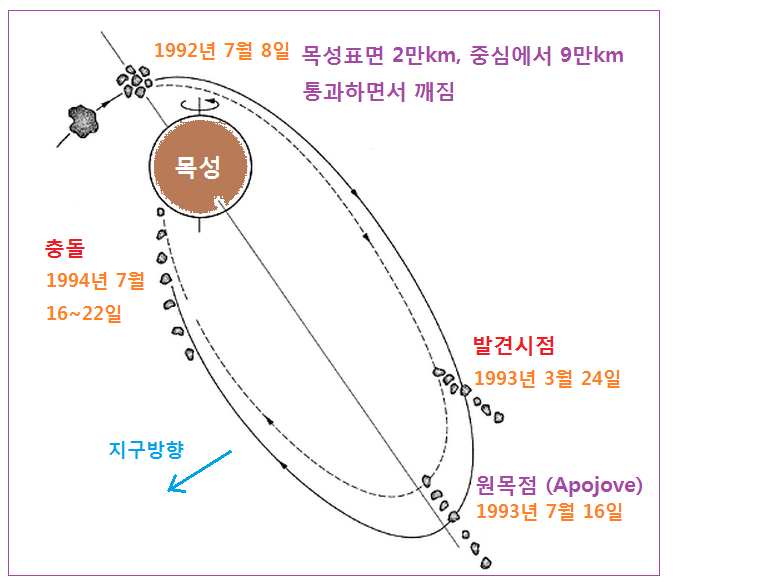
<Shoemaker-Levy 9 의 목성 충돌과정. 미국 시간.
ase.tufts.edu 의 그림에 일부 추가>
이 혜성은 그 이름처럼 Carolyn Shoemaker 와 그의 남편 Eugene Shoemaker 및 같이 연구하던 David Levy 세 사람이 미국시간 1993년 3월 24일에 발견했다. Shoemaker 부부 모두 천문학, 지질학 전공이며 이 혜성 발견에는 부인인 Carolyn 의 공적이 더 많아서 발견자를 표시할 때는 반드시 부인 이름을 앞에 쓴다. 과학계의 치열한 경쟁과 살벌한 서열을 볼 수 있는 대목이다. 아마도 등산 갈 때는 반드시 부인이 앞서 갈 듯.
이들 세 사람은 같이 연구하면서 무려 혜성 32개, 소행성 1,125 개를 새로 발견해낸다. 이 혜성은 나중에 <D/1993 F2>라는 공식 명칭이 붙었는데 일반적으론 <Shoemaker-Levy 9> 으로 부른다. 이름 뒤에 붙은 < 9 > 숫자는 이들 세 사람이 발견한 혜성들 중에서 <주기 혜성> 으로는
9 번째 혜성이란 뜻이라고. 한편 나중에 궤도추정 결과, 이 혜성은 이미 1970년대 부터 목성 궤도에 진입해서 주변을 돌고 있었다고 알려졌다.
흥미로운 것은 발견 당시에 이 혜성은 이미 21 조각으로 깨져있는 상태였고 발견 8 개월 전인 1992년 7월 8일에 이미 21 조각으로 깨졌을 것으로 계산되었다. 그런데 1992년 7월 8일에는 이 혜성이 발견되지도 않았는데 어떻게 단순한 궤도 추정만으로 이 혜성이 <정확히 그 날> 깨졌는지 알 수 있을까 ? 바로 이 문제가 앞으로 살펴보려는 <로쉬의 한계 Roche’s Limit> 라는 소재이다.
(3) 지구와 달의 경우
Roche’s Limt (로쉬의 한계) 란, 어떤 대형 천체에 가까이 접근하는 다른 소형 천체가 그 대형 천체의 <기조력> 으로 인해서 <파괴되기 시작하는 거리> 를 의미한다. 지구와 달 관계를 말하면, 달이 어떤 충격으로 궤도를 돌며 지구에 천천히 접근할 때, 달이 깨지기 시작하는 지구와의 거리이다.
아래 그림에서 Orbit 1 은 현재의 궤도를 말하고, Orbit 2 는 달이 지구 방향으로 궤도가 접근한 것이며 지구의 기조력 영향으로 달이 찌그러지면서 변형되기 시작한다. 이 경우 달은 완전히 딱딱하지는 않다고 가정한다. 완전히 딱딱한 것은 강체라고하며 아래에서 다시 설명 드린다.
Orbit 3 이 되면 달이 드디어 깨지지 시작하는데, 이 때 지구와 달 사이의 거리를 로쉬의 한계라고 한다. 한편 로쉬의 한계에서 <거리> 는 <대형천체 “중심”에서 소형천체 “중심”> 사이의 거리임에 유의하시면 된다.
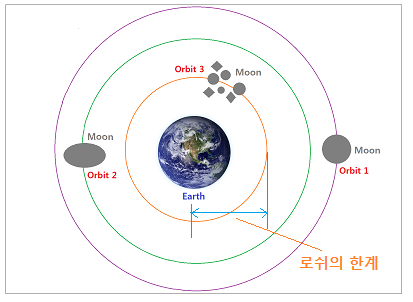
<지구와 달 사이의 로쉬의 한계>
만일 달이 공전운동 하면서 접근한다면 토성 고리처럼 지구에 고리 (Ring) 를 만들지도 모른다.
그러나 어떤 강한 충격으로 지구로 자유낙하하면서 접근한다면 슈메이커-레비 9 처럼 지구와 충돌하게 될 것이다. 그러나 달의 충돌을 크게 염려할 필요는 없을 것 같다. 달은 매년 3.8 cm 씩 지구에서 멀어지고 있으니까. 달이 지구에서 멀어지는 이유에 대해선 Serial No 12 를 참조하십시오.
달이 지구에서 멀어지고는 있으나 혹시 오랜만에 달 뒷면이 거대 소행성에 한 대 얻어맞아 지구 쪽으로 자유낙하 할지도 모르므로 아래 단락에서 지구와 달의 로쉬의 한계를 계산해 보겠다. 더불어 목성과 슈메이커-레비 9 의 로쉬의 한계도 같이 알아볼 것이다. .
(4) 로쉬의 한계 구하기
1. 로쉬의 한계 공식
로쉬의 한계는 프랑스 천문학자 Édouard Roche (1820~1893) 이 계산해낸 공식이다. 이 분은 대형 천체에 접근하는 소형천체를 강체와 유체 두 가지로 구분해서 공식을 유도했다. <강체 (剛體 Rigid Body)> 는 쉽게 말해서 딱딱한 고체를 뜻한다. 어느 정도 힘을 받아도 형태가 변하지 않는 물체이다. <유체 (流體 Fluid)> 는 말 그대로 흐르는 물체를 뜻하며 기체나 액체를 의미한다.

<Édouard Roche 초상>
로쉬의 한계 공식이 유도되는 과정이 크게 복잡하지는 않으나 역시 저의 한계를 넘는 사항이므로 그 과정은 생략하고 정리된 결과만 보여 드린다.
소형 천체가 강체인 경우
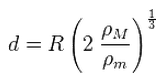
R 대형천체 반지름
ρM 대형천체 밀도
ρm 소형천체 밀도
소형 천체가 유체인 경우
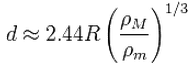
2. 지구와 달의 로쉬의 한계
그러면 지구와 달 사이의 로쉬의 한계를 구해본다. 필요한 수치는 아래와 같다.
달을 강체로 가정하고 공식을 적용한다.
R 지구 평균반지름 6,371 km
ρM 지구 밀도 5.51 gr/cm ³
ρm 달 밀도 3.34 gr/cm ³
d = 6,371 km x ( 2 x 5.51 gr/cm ³ / 3.34 gr/cm ³ ) x 1/3 승수
= 6,371 km x 1.49
= 9,492 km (약 9,500 km)
그런데 로쉬한계 d 는 두 천체 중심사이의 거리이다.
지구 평균반지름은 6,371 km 이고 달의 평균반지름은 1,737 km 이므로
지구 표면에서 달 표면까지 로쉬한계 거리를 D 라고 하면,
D = 9,492 km – (6,371 km + 1,737 km)
= 1,384 km
따라서 <달표면> 이 <지구표면> 에서 1,384 km 까지 접근하면 달이 깨져버릴 것이다.
3. 목성과 슈메이커-레비 9 의 로쉬의 한계
슈메이커-레비 9 을 강체로 가정하고 공식을 적용한다.
한편 슈메이커-레비 9 밀도는 1.25 gr/ cm ³ 으로 추정되었다.
R 목성 평균반지름 69,911 km
ρM 목성 밀도 1.33 gr/cm ³
ρm 슈메이커-레비 9 밀도 1.25 gr/cm ³
d = 69,911 km x ( 2 x 1.33 gr/cm ³ / 1.25 gr/cm ³ ) x 1/3 승수
= 69,911 km x 1.286
= 89,905 km (약 90,000 km)
이 거리를 AU 로 표시하면, 1 AU = 149,597,870,700 ± 3 meter
= 약 149.60 x 10 6 km
89,905 km / 약 149.60 x 10 6 km = 0.0006 AU 가 된다.
로쉬한계 d 는 두 천체 중심사이의 거리이다.
목성 평균반지름은 69,911 km 이고, 슈메이커-레비 9 반지름을 무시한다면
목성표면에서의 슈메이커-레비 9 표면까지 거리는
D = 89,905 km - 69,911 km
= 19,994 km (약 20,000 km)
따라서 <슈메이커-레비 9> 이 <목성표면> 에서 19,994 km (약 20,000 km) 까지
접근했을 때 깨졌다는 추정이 가능하다. 슈메이커-레비 9 궤도를 계산하면 이 거리를
통과한 시점이 1992년 7월 8일로 나오게 된다.
그런데 우주 모든 위성들은 로쉬의 한계 바깥에서만 모행성을 공전하고 있을까 ? 세상살이에는 반드시 예외가 있듯이 로쉬의 한계 안쪽에서 노는 위성들도 있다. 우리 태양계의 예를 들면 목성의 위성인 Metis 와 토성 위성 Pan 등이 그런 것들이다. 이런 경우는 위성의 점성이 매우 커서 목성이나 토성의 엄청난 기조력을 견뎌내기 때문이라고 한다.
로쉬의 한계를 남녀간에도 적용할 수 있을 지 생각해 보았다. 서로 좋아한다면야 하루종일 붙어 있고 싶겠으나 Feel 이 통하지 않는 경우에 로쉬의 한계는 어떻게 될까 ? 사람의 부피를 계산해서 구체로 표시한 다음에 반지름을 구하고 사람 각각의 밀도를 추정한 후에, 유체 경우의 로쉬의 한계 공식을 적용하면 될 것이다. 이 거리를 알고 있으면 더운 날씨에 괜히 다치지 않고 적당한 거리 유지하면서, 단계적으로 접근하는 전략을 세울 수 있을 듯하다.
III. Coffee Break
1 분각, 1 초각은 어느 정도 크기일까 ?
(1) 각거리를 표시하는 기호들
천체간의 각거리 (Angular Distance) 를 표현할 때는 <도, 분각, 초각> 이란 용어가 사용된다. 여기서 <도 ( ° ) > 는 일상 생활에서도 측정 가능하므로 그 크기를 머리 속으로 충분히 짐작할 수 있다. 또한 도구 없이 손으로만 밤하늘 별들 각거리를 대충 잴 때 새끼 손가락은 1 도, 가운데 세 손가락을 붙이면 5 도, 주먹은 10 도 정도로도 사용한다.
그러나 1 도를 60번 쪼갠 1분각 또는 1도를 360번 쪼갠 1초각은 망원경으로 관측할 때 및 천체사진, 컴퓨터 프로그램, 적도의 주기오차 (Periodic Error) 등에서는 사용되지만 일상에서 그 크기가 어느 정도 되는지 상상하기 쉽지 않다. 최근 해외잡지에 이들 미세한 각거리를 동전크기에 비교한 기사가 있어 이를 우리나라 <100 원 동전> 크기로 환산해서 계산해 보았다. 우선 이들 각거리를 표현하는데 사용되는 기호를 먼저 알아본다.
<각거리를 나타내는데 사용되는 경우>

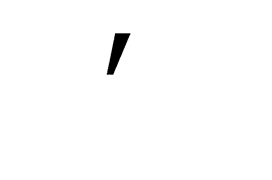

------------------------------------------------------------------------------------------
우리말 기호명칭 도 없음 없음
우리말 발음 도 분각 초각
영어 기호명칭 Degree Prime Double Prime
영어 발음 Degree Arcminute Arcsecond
크기 원의 1/360 <도> 의 1/60 <분각> 의 1/60
영어 약자 Deg Arcmin 등 Arcsec 등
-------------------------------------------------------------------------------------------
참고로 일반적으로 잘 사용되지 않는 단위이지만 <밀리 초각 (Milliarcsecond)> 은 <초각> 의 1/1,000 이고 <마이크로초각 (Microarcsecond)> 은 <초각> 의 1/1,000,000 이다.
(2) 100원 동전으로 계산한 각거리
그러면 우리나라 100 원 동전이 얼마나 떨어져 있어야 위의 각거리가 되는지 알아본다.
우선 각도기에 표시된 < 1 °> 크기를 한 번 보시지요.
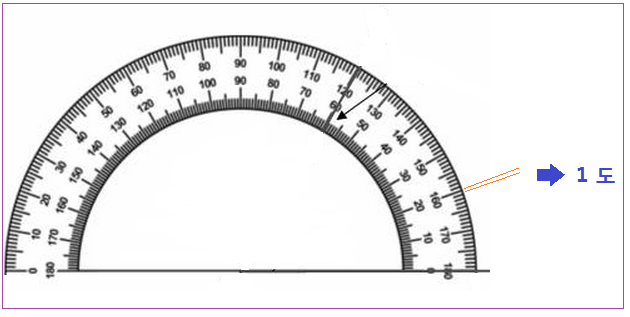
<각도기에 표시된 1 °>
우리나라 100 원 동전 지름은 정확히 24.00 mm 이다. 그런데 미국의 25 cent 동전 (Quarter) 으로 < 1 °> 를 측정하면, 1.39 meter 떨어진 거리에서 보이는 동전의 각거리라 한다. 25 cent 동전 지름은 24.26 mm 이다. 따라서 우리 100 원 동전으로 환산하면 1.375 m 가 된다. 따라서 1 m 37.5 cm 거리에서 보이는 100 원 동전의 지름이 < 1 °> 각거리가 된다.
<1 분각 (1’ 또는 1 Acrmin)> 이 되려면 1.375 m x 60 = 82.5 m 가 되어 약 83 m 이고,
<1 초각 (1” 또는 1 Acrsec)>은 82.5 m x 60 = 4,950 m 가 되어 4 km 950 m, 약 5 km 가 된다.
우리가 가끔 쉽게 말하는 <1 초각> 이란 약 5 km 거리에서 보이는 100 원 동전의 지름이다.
정리하면 아래와 같다.
1 도 1 m 39 cm
1 분각 82 m 50 cm
1 초각 4 km 950 m
저의 문제는 눈이 나빠 82 m 거리에서도 100원 짜리가 보이지 않는다는데 있다. 앞으로 별 사이 각거리를 말할 땐 제가 결코 “범접할 수 없는” 거리들이므로 조금이나마 경건한 자세로 말해야겠다.
IV. Surprise & Mystery
W49B – 우리은하 최연소 블랙홀
(1) 우리은하 20 번째 블랙홀
작년 2012년 8월에 올린 Serial No 10 에서는 그 때까지 발견된 우리은하 내부의 블랙홀이 19개라고 말씀 드렸었다. 물론 실제로는 이보다 한참 더 많을 것이지만 이 정도 숫자밖에 안되는 이유는 블랙홀이란 것이 빛을 내지 않으므로 찾기 어렵기 때문이다. 사실 발견되어 있는 블랙홀 중 1 개만 제외한 18개 모두 그 옆에 자신의 구성물질을 블랙홀로 내보내는 동반성이 있다. 나머지 1 개는 우리은하 중심부 블랙홀인 Sagittarius A * 이다. 이 19개 블랙홀 목록은 Serial No 10에 있으므로 참조 바랍니다.
한편 네덜란드에서 미국으로 이주한 전파 천문학자인 Gart Westerhout (1927~2012) 라는 분이 전파를 발산하는 천체를 1958년에 하나 찾아냈는데 최근 망원경 발전에 따라 그 천체의 신비한 모습을 조금씩 더 알게 되었다. 그런데 5개월 전인 2013년 2월 10일에 발행된 Astronomical Journal 에 실린 논문에서 이 천체가 우리은하 내부의 블랙홀일 “가능성” 이 있다고 발표되었다. 바로 이 천체가 <W49B> 이며 “W” 는 발견자 Westerhout 의 이니셜이다. <3C 398> 이라고도 불린다. “C” 는 Cambridge Catalogue of Radio Source 의 약자. 아래에 Gart Westerhout 의 모습 올려드립니다.


<Gart Westerhout 중년 모습> <Gart Westerhout 노년 모습
사진 The American Astronomical Society>
아래 사진은 W49B 의 합성한 후의 사진과 합성 전의 사진들이다. 적외선 사진 보시면 꼭 45° 각도로 기울인 드럼통 같다. 서양에선 이 천체 모습을 포도주나 위스키를 수성시키는 오크통 (Oak) 같다고 해서 Oak Barrel 또는 그냥 Barrel 이라 부른다.
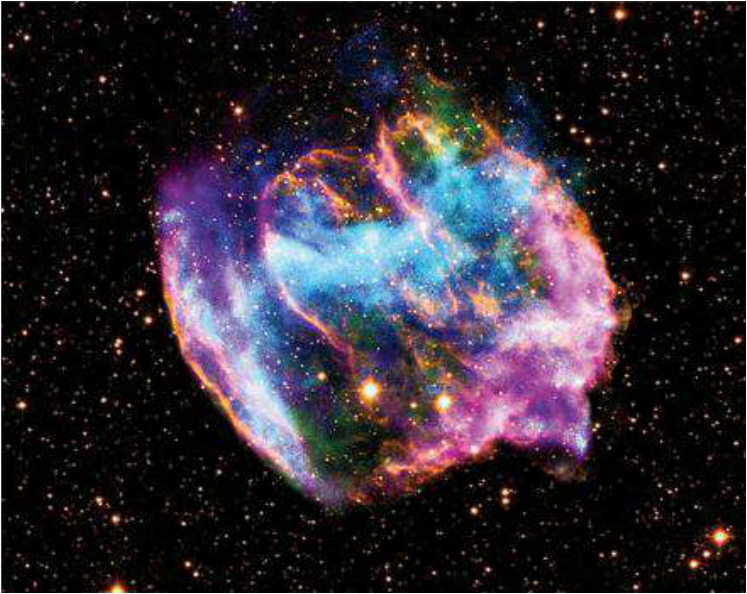
<W49B – 3장 사진 합성 후 모습. 사진 Chandra X-ray Obs.
적경 19/ 11/ 07. 적위 + 09/ 06/ 00. Aquila (독수리 자리). 거리 26,000 광년>
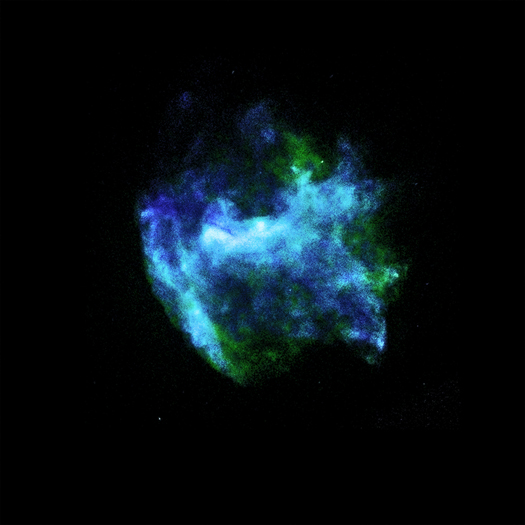
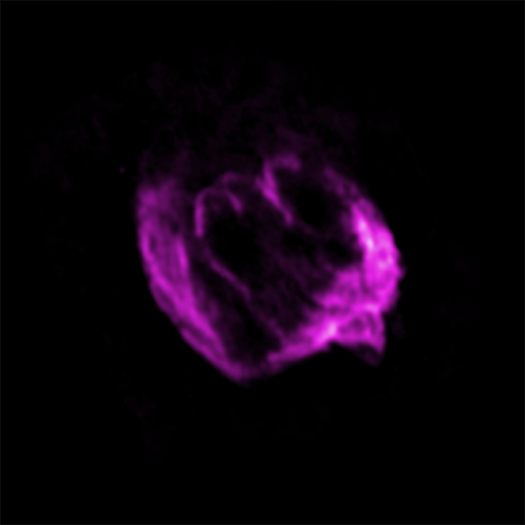
<X- ray. 사진 Chandra X-ray Obs.> <Radio. 사진 Very Large Array>
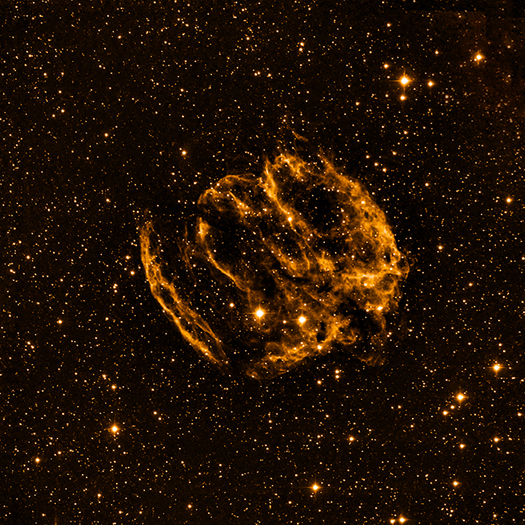
<Infrared. 사진 Palomar Obs.>
W49B 는 초신성 폭발 잔해이다. 이 별은 지금부터 약 1,000년에 초신성 폭발했을 것으로 추정된다. 정확히 1,000년전이라면 AD 1013년인데 이 즈음에 폭발한 유명한 초신성이 생각난다. AD 1054년에 폭발한 <M1 게성운, Crab Nebul>. 이것도 신비한 면이 많아 “Messier One” 대신 “Mysterious One” 으로도 불린다.
하여간 별이 초신성으로 폭발하면 그 별은 중성자성이나 불랙홀이 된다. 초신성 잔해에서 중성자성이 관측되는 대표적인 것이 M1 게성운인데, 허블 가시광선 망원경 사진에서는 중심성 찾기가 어렵지만 적외선으로 찍으면 중심성이 잘 나타난다. 아래 사진은 허블망원경과 스피처 적외선 우주망원경 사진을 합성한 것이다. 성운 가운데의 중성자성 주변부가 보이실 것이다.
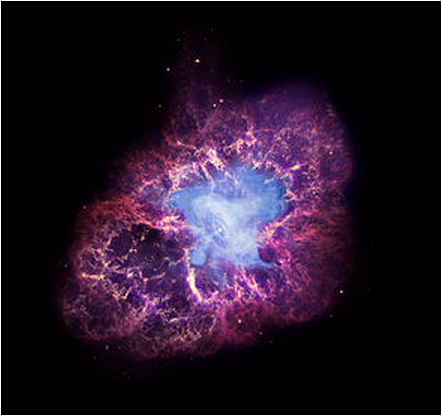
<M1 Crab Nebula. Hubble and Spitzer Infrared Space Telescope 사진 합성. 사진 NASA>
(2) 1,000 살이 최연소 ?
그런데 W49B 의 X-ray, 적외선 및 전파 망원경 사진을 아무리 자세히 보아도 그 중심부엔 아무것도 보이지 않는다. 별이 초신성으로 폭발하면 그 폭발한 별은 중성자성이나 불랙홀이 되므로
중성자성이 없으면 남은 카드는 블랙홀 밖에 없을 것이다.
여러 관측 Data 로 추정한 결과, 여기에 블랙홀이 있다는 것이 Astronomical Journal 2월호에 실린 논문의 결론이다. 이것이 사실이라면 W49B 가 우리은하에서 가장 나이 어린 블랙홀일 가능성이 있다. 물론 이 나이는 이 천체까지의 거리 26,000 광년을 감안하지 않고, 오직 지구에서 볼 때 1,000년 전에 초신성 폭발이 일어났다는 추정에 따른 것이다.
“1,000 살 최연소 ”를 인간 수명에 적용하면 말이 안될 것이다. 더욱이 최연소 블랙홀이란 타이틀은 단지 “우리은하” 에서만 통한다는 것을 기억하실 일이다. 우리은하도 크지만 우주는 비교할 수 없이 더 크고 더욱이 아직 우리 눈에 그 빛이 도착하지도 않은, 우리가 모르는 광활한 우주도 있기 때문에. 하여간 우리은하에서 블랙홀이 몇 개인지 궁금하시면 “인류가 아는 것은 단지 20 개 뿐” 이라고 알고 계시면 되리라 믿는다.
V. Journey to Deep Sky
잃어버린 별자리를 찾아서 (7 회)
Turdus Solitarius 와 Noctua (지빠귀자리와 올빼미자리)
(1) Turdus Solitarius 가 사는 곳
“Journey to Deep Sky” 공간을 빌려서 “잃어버린 별자리를 찾아서” 를 게재합니다.
<Turdus Solitarius> 는 어떤 <새 (Bird)> 이름의 라틴어이다. 고유명사 새 이름이라 저도 생소하므로 먼저 명칭에 대해 조사한 내용을 간단히 설명 드린다. 라틴어 <Turdus> 는 영어로 Thrush 이며 <딱새 또는 지빠귀> 를 말한다고 한다. <Solitarius> 는 영어로 Solitaire 이고 Thrush 와 같은 의미로 <딱새 또는 지빠귀> 의미이다. 라틴어인 이 두 단어 별자리를 영어로 표시할 때는 Turdus 는 빼고 그냥 <The Solitaire> 로 쓴다.
저는 새에 대해선 문외한이라 딱새와 지빠귀의 정확한 차이를 알지 못한다. 아마도 지빠귀는
딱새과 (科, Family) 에 속한 여러 새들 중의 한 종류로 보인다. 여기서는 딱새 대신에 <지빠귀>란 이름으로 사용하겠다. 우선 이 별자리 모양부터 알아본다.
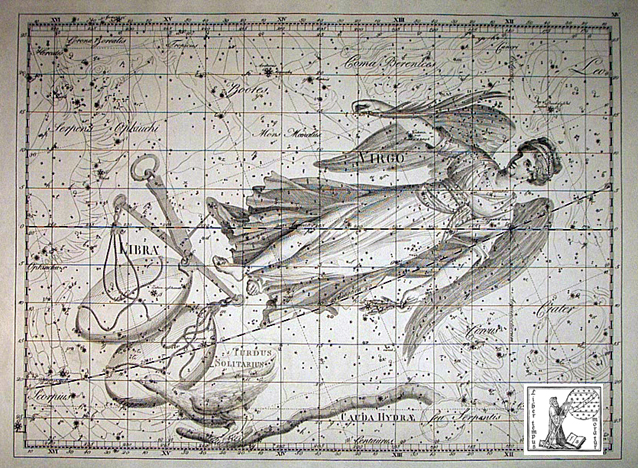
<Bode 의 Uranograhpia 1801년> >
위 성도는 1801년에 Johann Bode 가 발행한 Uranograhpia 인데, 왼쪽 아래에 새 한마리가 보인다. 이 새가 <Turdus Solitarius> 로서 새가 않아 있는 것은 나뭇가지가 아니라 Hydra 의 꼬리이다. 바다뱀 꼬리에 용감하게 앉아 있으니 목숨에 대해 아무 개념 없는 새인 것 같다. 아래는 이 부분을 확대한 그림이다.
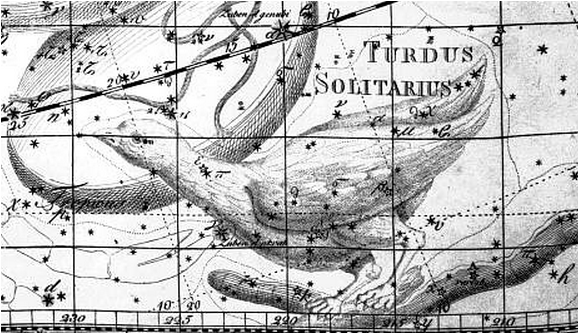
<Bode 의 Uranograhpia 부분확대. 그림 ianridpath.com>
현대 성도에서 이 별자리 위치는 아래와 같다.
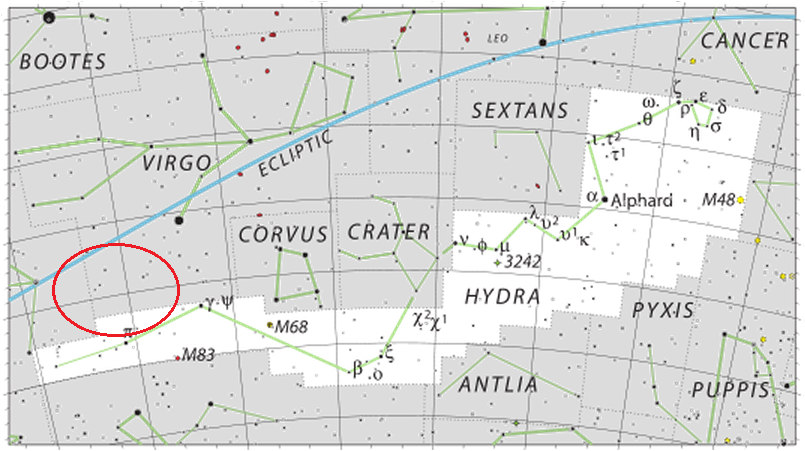
<현대 성도에서의 Turdus Solitarius 위치. Sky & telescope 성도에 붉은색 원 표시>
(2) 지빠귀 정체에 대한 논란
이 별자리는 프랑스 천문학자 Pierre-Charles Le Monnier (피에르 샤를 르모니에 1715~1799) 작품이다. 프랑스 왕립과학원이 1776년에 발행한 논문집에 실린 그의 논문 <Constellation du Solitaire> 에 처음 기록이 보인다. Le Monnier 는 이 논문에서 Hydra (바다뱀자리) 꼬리부분의 22 개 별들로 목록을 만들어 놓았다. 참고로 프랑스 왕립과학원 논문집 이름은 <Mémoires de l’Académie Royale des Sciences 1776>.
그런데 이 새가 정확히 어떤 새인지를 놓고 자료에 따라 틀린 기록이 보인다. 현재 프랑스 국립도서관에 있는 이 논문집에는 그가 “인도양 Rodrigues Island (로드리게스 섬) 으로 항해한 것을 기념해서 만들었다” 는 설명이 있으며 추가로 “동남아시아 (인도네시아, 필리핀 등) 에 사는 새 (Bird of the Indies and Phlippines” 라는 언급과 함께 Le Monnier 가 직접 그린 그림이 실려 있다. 여기서 Indies 는 지금의 인도가 아니고 베트남, 라오스 등 인도차이나 반도 및 인도네시아, 필리핀 지역을 말한다. Le Monnier 가 직접 그린 새 그림은 아래와 같다.
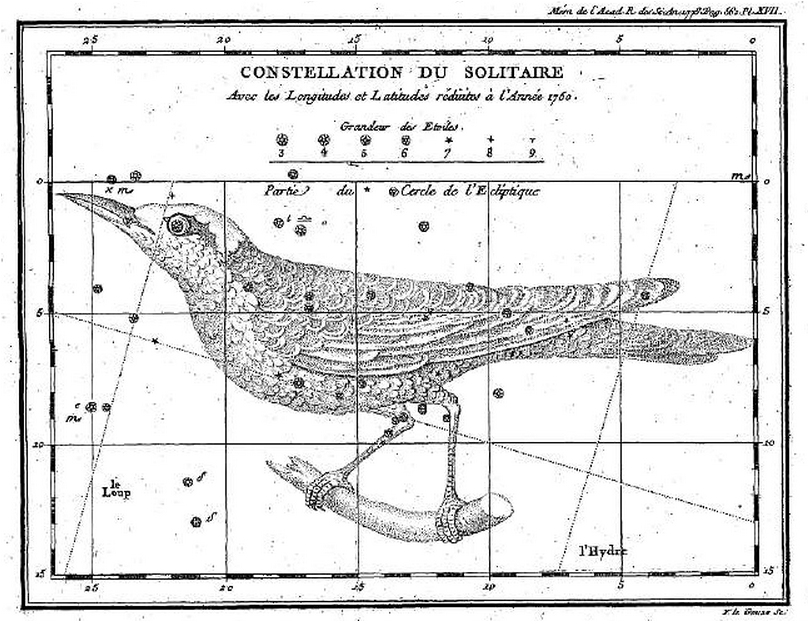
<Le Monnier 가 직접 그린 Turdus Solitarius.
그림 copyright : Bibliotèque nationale de France. ianridpath.com 에서 인용>
위에서 이 별자리 라틴어 이름 <Turdus Solitarius> 는 영어로 Thrush 이고 우리말로는 지빠귀라고 말씀 드렸다. 따라서 <Thrush (지빠귀)> 종류 새 중에서 위 그림과 가장 비슷한 새를 찾으면 될 것이다. <Blue Rock Thrush> 라는 새가 이것과 가장 유사한데, 특히 암컷이 그림과 가장 닮아 보인다. 우리나라에도 이 새가 서식하지만 사진에 모두 저작권이 있어서 다른 나라에서 찍은 공개된 사진만 올려 드린다.


<Blue Rock Thrush 암컷. 촬영지 일본> <Blue Rock Thrush 수컷. 촬영지 스페인>
이 새가 정확히 어떤 새인지를 놓고 자료에 따라 틀린 기록이 나타나는 이유는 Le Monnier 가 그의 논문에서 “이 별자리는 인도양 Rodrigues Island 으로 항해한 것을 기념해서 만들었다” 는 언급 때문인 것 같다. 실제로 Le Monnier 는 1761 년 금성 일면통과를 관측하기 위해 인도양 Rodrigues Island 를 방문하고 이후에 동남아시아까지 항해했었다. Rodrigues Island 는 프랑스의 인도양 공략 거점인 Mauritius 동쪽에 있다. 1761년 금성 일면통과와 관련된 유럽열강의 치열한 경쟁에 대해선 Serial No 7 을 참조하십시오. 그러면 Rodrigues Island 가 어디 붙어 있는지 그 위치부터 살펴본다.
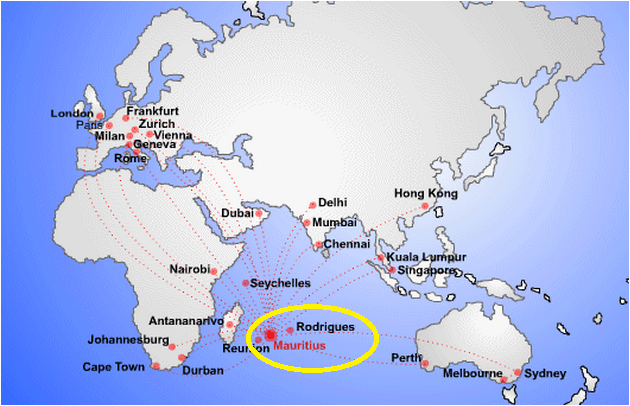
<Rodrigues Island 위치. Mauritius 동쪽>
실제로 예전 Rodrigues Island 주변 광범위한 지역에 <Rodrigues Solitaire> 라는 새가 있기는 있었다. 이 새의 이름에 Rodrigues 라는 지역과 Solitaire 라는 이름이 들어가 있으니 충분히 혼동할 만하다. 그러나 이 새의 정체를 밝히려면 Le Monnier 가 그의 논문에서 별도로 언급한 “동남아시아에 사는 새” 라는 부분과 그의 스케치를 같이 살펴보았어야 한다.
Rodrigues Solitaire 라는 새는 1730년대 또는 1760 년대에 이미 멸종했다고 알려져 있다. 유명한 <Dodo (도도)> 새와 혈통으론 친척지간이다. 도도새도 이미 멸종했다. 만일 Le Monnier 가 정말로 이 새를 1761년에 Rodrigues Island 에서 보았다면 멸종 직전의 새를 본 것인데, 그가 그린 스케치와 Rodrigues Solitaire 는 모습이 완전히 다르므로 이 새를 묘사한 것은 아니라고 보아야 한다.


<Rodrigues Solitaire 새. 이미 멸종> <Dodo 새. 이미 멸종>
(3) 그리이스 신화의 <아테나 여신 올빼미 (Athena Noctua)>
한편 영국의 Alexander Jamieson 은 1822년 Celestial Atlas 출간하면서 이 별자리를 <Noctua> 로 바꾸어 놓았다. Noctua 는 Little Owl (올빼미) 의 라틴어이다. Alexander Jamieson 이란 인물은 프로가 아니고 아마추어 천문학자이다. 아마추어이므로 “정통 학계”가 뭐라 하든지 신경 쓸 일 아니고, Turdus Solitarius 가 어떤 새인지에 대해서도 당시 논란이 많으니 “누구나 알고 있는” 다른 새로 바꾸고 싶었던 것 같다.
아래에 Noctua 가 등장하는 성도 Celestial Atlas 를 올려 드린다. 올빼미 오른쪽에 보이는 새는 까마귀 (Corvus) 이다. 이 까마귀도 다음 단락에서 중요한 주인공으로 등장하므로 잘 살펴 보십시오.
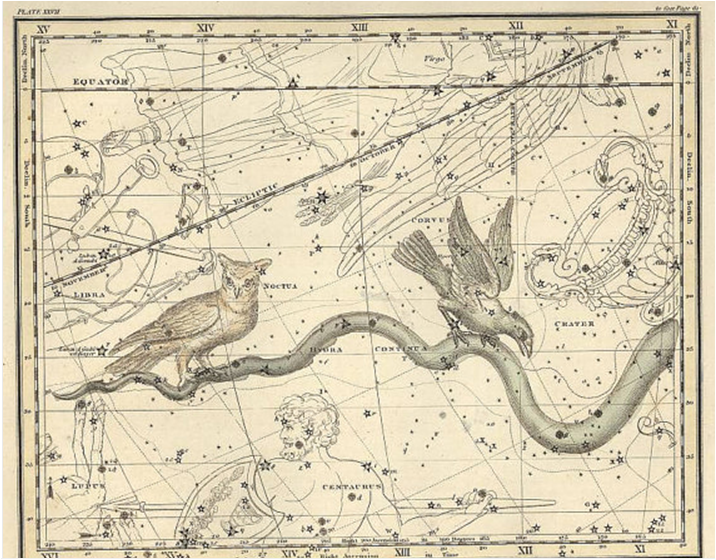
<Alexander Jamieson. Celestial Atlas 1822 그림 etsy.com>
Jamieson 은 어떤 새의 배경에 깔린 이야기를 전세계 사람들 누구나 알고 있어야 한다고 생각했을 것이다. 그러면 그런 새를 어디서 골라야 할까 ? Jamieson 이 간 곳은 역시 별자리에 많이 인용되는 그리이스 신화였다. 이 신화에 나오는 새들 중 <독수리> 는 이미 별자리에 있으므로 아마도 Athena 여신의 동반자인 <Noctua> 를 선택한 듯하다. Athena 여신은 Athene 으로도 쓴다. Noctua 는 영어로 Little Owl 인데, 우리말로 이 올빼미를 무어라 부르는지 찾아보았더니 “작은 올빼미” 가 아니고 <금눈쇠 올빼미> 라고. 하여간 이 올빼미가 성도 그림과 같은 지 실제 모습 한 번 보시지요.

<Noctua (Little Owl) 의 실제 모습>
그리이스 신화에서 Noctua (올빼미) 는 Athena 또는 Athene 여신의 동반자나 여신 그 자체로 묘사된다. Athena 여신이 “지혜의 여신” 이므로 이 올빼미도 “지혜”를 상징하는 동물로 묘사된다.
아래 그림은 그리이스 신화가 그려진 BC 480 년경 도자기이다. Athena 여신 왼쪽에 Noctua 가 보인다. 여신의 가슴 부분에 이상한 낙서 같은 그림이 있는데 어떻게 들어간 것인지 확인할 수는 없었다.
그 아래 동전 사진은 BC 490 년경의 도시국가 아테네의 화폐이다. 동전에 새겨진 단어는 <AθE> 이고, <AθENAIΩN> 의 약자이며 영어로는 “Of the Athenians“ 이라 한다. 동전 가운데에 Noctua 가 있으므로, 같이 읽으면 “Noctua of the Athenians ” 가 된다. 우리말로는 “도시국가 아테네인들의 올뺴미” 이다. 지혜를 존경하던 당시 아테네 인들의 정신세계가 짐작된다.


<Athena 여신의 동반자인 Noctua (올빼미). <도시국가 아테네의 동전. BC 490 년경>
BC 480 년경 도자기> >
(4) 로마 신화의 <미네르바 부엉이 (Minerva Noctua)>
저는 Alexander Jamieson 의 성도를 보면서 왜 그가 굳이 다른 새도 아닌 “올빼미” 로 바꾸어 놓았는지 그 의도가 궁금하던 중에 독일 철학자 Hegel 의 말이 생각났다. 제가 오버하는 것은 알지만 더운 날씨에 여유 좀 가지려 “저 혼자 추정한” 그의 의도를 설명 드리려 한다.
위에서 그리이스 신화에 나오는 Athena 여신의 Noctua (올뺴미) 는 “지혜” 를 상징한다고 말씀 드렸다. 로마시대에 들어 그리이스 신화는 로마 신화로 변형되어 Athena 여신은 Minerva (미네르바) 로 이름이 바뀌게 된다. 그런데 로마신화에서 Minerva 여신이 데리고 다니던 새는 원래
<까마귀> 였다. 헌데 이 까마귀가 죄를 지어 쫒겨 나고 Minerva 는 대신 Noctua (올빼미) 를 데리고 다니게 된다. 이런 이유로 로마신화에서도 Minerva 여신의 올빼미는 그리이스 신화의 올빼미 개념도 그대로 “지혜” 의 상징이 되어 있다.
Minerva 가 데리고 다니던 올빼미는 원래 여자 사람이었는데, 역시 지은 죄가 있어서 벌을 받아 올빼미가 되었으며, 그 죄가 부끄러워 낮에는 조용히 있다가 깜깜한 밤이 되어야 활동한다고 한다. 이 올빼미가 지은 죄는 근친상간이다. 하여간 지혜의 여신인 Minerva 덕분에 이 올빼미도 지혜의 상징으로 되었으니 명예회복은 된 셈이다.
혹시 “미네르바의 부엉이는 황혼이 되어야 날개를 편다” 라는 말을 들어보신 적 있으신지요 ?
이 말은 독일 철학자 헤겔 (Hegel. 1770~1831) 이 1820년 출간한 책 <법철학 (Grundlinien der Philosophie des Rechts>에 나오는 말이다. 헤겔의 본명은 Georg Wilhelm Friedrich Hegel.
올빼미는 우리말로 “부엉이” 로 번역하기도 하는데, 경음을 피하고 부드러운 어감 때문인 것 같다.
하여간 헤겔은 “지혜” 를 그의 전공인 “철학” 과 같은 의미로 보았다. 헤겔의 말은 “철학이란 불확실한 미래를 예측하는 것이 아니고 적정한 조건이 갖춰진 시점 (저녁 때, 황혼) 이 되어야 그 의미가 분명해진다” 라는 뜻이라고 한다. 우리말로 써 있다고 제가 그 뜻을 이해하는 것은 아니므로 여기까지 하고 그냥 넘어가겠다. .
제 생각에 Alexander Jamieson 은 <Turdus Solitarius> 별자리을 다른 새로 바꾸고자 생각하던 중에 아마도 그 옆의 까마귀 (Corvus)> 보고 로마 신화의 Minerva 까마귀가 생각났는지도 모를 일이다. 그러나 로마 신화에서도 까마귀는 올빼미 (부엉이) 로 바뀌어져 있고, 그 개념도 그대로 “지혜” 이므로 올빼미로 바꾸어도 좋다고 생각했을 수도 있다.
한편 헤겔이 <법철학> 책을 출간한 연도가 1820 년이고, Jamieson 이 Celestial Atlas 출간한 해는 1822년 이므로 Jamieson 이 헤겔의 <법철학> 을 읽어보았을 가능성도 있다. 그가 독일어도 하는지 알 수 없지만…. “꿈보다 해몽” 이란 말처럼 Jamieson 성도를 보다가 헤겔이 말이 생각나서 한 말씀 드려 보았다.
(5) 밤하늘의 아홉 마리 새들
그런데 Athena 여신의 올빼미가 거의 모든 그림, 조각에서 “왜 옆으로 앉아 오른쪽으로 고개를 돌리고 정면을 보는 자세” 인지 궁금하다. 몇 가지 자료를 뒤졌으나 속 시원한 대답을 찾을 수 없었다. 아마도 그 자세가 올빼미의 전체 모습을 보여주기에 가장 적절하기 때문인지도 모르겠다.
하여간 정체에 대해 논란이 많았던 Turdus Solitarius 나 Noctua 모두 1929년 퇴출되었다. 지빠귀나 올빼미 한 마리가 없어져도 아직도 밤하늘에 새가 아홉 마리나 된다. 좀 많은 것처럼 보이지만, 그 이유는 아마도 인류가 “새” 라는 동물을 그만큼 신비하게 생각했기 때문일 것으로 생각된다.
개인적으로도 새에 대해 가만히 생각해보면, 신체 각 부분이 비행에 적합하도록 진화한 그들 능력이 정말 신기하게 보인다. 아마도 이런 이유 때문에 전 세계에 “아마추어 조류학자” 도 “아마추어 천문학자” 에 못지않게 많은 것으로 생각된다. 끝으로 밤하늘에 사는 아홉 마리 새 이름들을 열거해 드립니다. 어떤 새들이 사는지 다시 한번 살펴 보십시오.
극락조 Apus 독수리 Aquila 비둘기 Columba
까마귀 Corvus 백조 Cygnus 두루미 Grus
공작 Pavo 불사조 Phoenix 큰부리새 Tucana
VI. Moon River Wider Than a Mile
Apollo 11 호 우주비행사 Crater 찾기
(1) 고요하지만은 않은 고요의 바다 주변
지난 6월 중순, 어느 문화센터에 천문강의 나오신 서울지부장님 및 다른 운영진분들과 점심식사 하는 자리에서 달착륙 순간을 TV로 보던 때의 감흥을 서로 얘기하던 기회가 있었다. 당시 어느운영진 분께서 Apollo 11 호가 달착륙 하던 때가 7월달로 기억된다고 말씀하셨는데, 며칠 후 다른 자료를 찾다가 우연히 그 날이 미국시간으로 7월 20일임을 알게 되었다. 어차피 7월호 칼럼 소재 준비가 안되어 있던 때라 예전에 어디서 한 번 보았었던 Apollo 11 호 우주비행사들 이름을 딴 Crater 들을 소재로 칼럼을 마련했다. 더불어 그 주변에 흥미로운 지형이 하나 있는데, 이것도 같이 소개 드리려 한다.
Apollo 11 호 우주비행사들 이름을 딴 Crater 들은 인터넷 등 자료를 찾으면 나오지만 너무 작아서 웬만한 월면도에는 표시되어 있지 않다. 더욱이 이들 Crater 는 예전에 다른 이름들이 붙어 있었으나 달착륙 이후에 Apollo 11 호 우주비행사들 이름으로 개명되었고, IAU 의 공식인정을 받았다.
1969년 7월20일 Apollo 11 호가 착륙한 곳은 <고요의 바다 (Mare Tranquillitatis / Sea of Tranquillity)> 서남쪽인데, 우선 달 전체에서 그 위치가 어딘지부터 찾아본다. 아래 사진에서 노란색 사각형의 중심부가 착륙장소이다. 참고로 우주비행사가 달착륙을 시도한 Apollo 우주선은 1969년의 11호부터 1972년 17호까지 있었고 13호를 제외하고는 모두 착륙에 성공했다.

<사진 1 Apollo 11 호 착륙지점 주변>
아래 사진은 위 그림에서 노란 사각형 부분을 확대한 것이다. 사진에서 <11> 이라고 표시된 장소가 Apollo 11 호 착륙지점이다. 세 명 우주비행사 이름의 Crater 가 있다면 분명히 착륙지점 부근일 것이다. 바로 그 아래 <사진 3> 에서 위치를 표시해 놓았다.

<사진 2 첫번째 사진 내부의 노란 사각형을 확대한 것. 달지도: 원치복 서울지부장님>
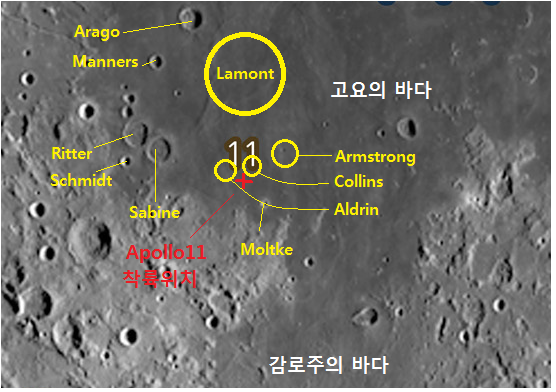
<사진 3 위 사진에 보이는 지형 이름들. 원치복 서울지부장님 달지도에 추가>
바로 위 사진에서 붉은 색 십자표시가 실제 착륙지점이다. 한편 착륙지점 북쪽에 Apollo 11 호 우주비행사 세 명 이름을 써 드렸는데, 어인 일인지 <Armstrong> 표시 원 안에는 점 같은 Crater 가 보이지만 <Aldrin> 과 <Collins> 표시 원 내부에는 <사진 2> 와 비교하셔도 아무것도 보이지 않으실 것이다. 참고로 우주비행사 세 명의 정식이름은 Neil Armstrong, Buzz Aldrin,
Michael Collins 이다. 비록 이 사진에선 보이지 않아도 그 위치에 “Crater” 가 있기는 있다.
또한 <Lamont> 로 표시한 원 부분을 <사진 2> 와 비교해도 용암 평원만 보이지만, 그래도 여기에 “뭔가 있기는 있으므로” 아래 부분에서 설명 드리겠다. 고요의 바다를 멀리서 보면 고요한 듯하지만 가까이서 보니 그 주변에 딸린 식구들은 만만치 않아 보인다.
(2) 아직도 우리는 한 팀 - Armstrong, Aldrin, Collins
다음 사진은 Aldrin, Collins 및 Armstrong Crater 지역을 확대한 것이다. 바로 위 사진에서 Moltke Crater 를 기준으로 위치를 비교해 보십시오. 이 지역의 거리 및 크기가 짐작되시도록 아래에 다른 Crater 로부터 각 Carter 들까지 거리를 정리해 드린다.

<사진 4 Aldrin, Collins 및 Armstrong Crater 지역 확대 사진. NASA>
Crater 예전 이름 직경 / 깊이 착륙지점에서 거리
----------------------------------------------------------------------------------
Aldrin Sabine B 3.4 km / 0.6 km 북서쪽 50 km
Collinsl Ollie Woods 2.4 km / 0.6 km 약간 북동쪽 25 km
Armstrong Sabine E 4.6 km / 0.7 km 북동쪽 45 km
-----------------------------------------------------------------------------------
아래는 Crater 이름들을 뺀 깨끗한 사진이다.

<사진 5 Crater 이름들 삭제한 사진. NASA>
그러면 이 지형들을 지구에서 망원경으로 관측하려면 7월중에는 어느 날이 제일 좋을까 ? 이 지형들은 소형 Crater 들이므로 Terminator 가 이 지역을 지나가는 때가 최적일 것이다. 천문력을 찾아보니 월령 5.2일, 6.2일인 7월13일과 14일 이다. 나머지는 망원경 성능이 관건이 되겠지만.
추가로 달 궤도 우주선에서 찍은 Apollo 11 호 착륙선 잔해 한 번 보시지요. 달착륙 음모론에 반박하는 자료로도 사용되는 사진인데, 해상도가 좋지 않아 물체가 뭔지 알아볼 수는 없다. 다만 “거기 뭔가 있다” 는 정도로 만족해야 할 듯. 사진에 나오는 용어를 아래에 정리했다.
달 궤도 우주선 : Lunar Reconnaissance Orbiter
LRRR : Lunar Laser Ranging Experiment (레이저 측정기)
PSEP : Passive Seismic Experiment Package (지진파 탐지기)

<사진 6 Lunar Reconnaissance Orbiter 에서 찍은 달 착륙선 잔해. 사진 NASA>
(3) 고요하게 사시는 귀하신 분 Lamont
위의 <사진 3>에서 Lamont 표시한 부분은 그냥 평범한 용암대지로 보이지만, 이 지형이야 말로 한 번 보려면 많은 노력이 필요한 “귀하신 분” 이다. 그 이유는 Aldrin, Collins, Armstrong Crater 처럼 Termonator 가 이 지역에 걸쳐 있을 때라야 그 신비한 모습을 보여주기 때문이다. 더욱이 Lamont 는 옷을 두 벌 겹쳐 입고 있는데, 바깥쪽 옷은 너무 얇아 보기가 더욱 쉽지 않다.
이 지형은 용암이 안쪽 Rim 에서 넘쳐나면서 주변으로 흘러나가 외곽 Rim 까지 채운 모습을 잘 보여준다. 월령이 7일을 넘어가면 태양이 이 지역을 바로 위에서 비추므로 그 때부터는 <사진 2> 에서 보이듯이 평범한 용암대지로 모습을 바꿀 것이다. 아래에서 Lamont 의 신비한 모습 잘 관찰해 보십시오.
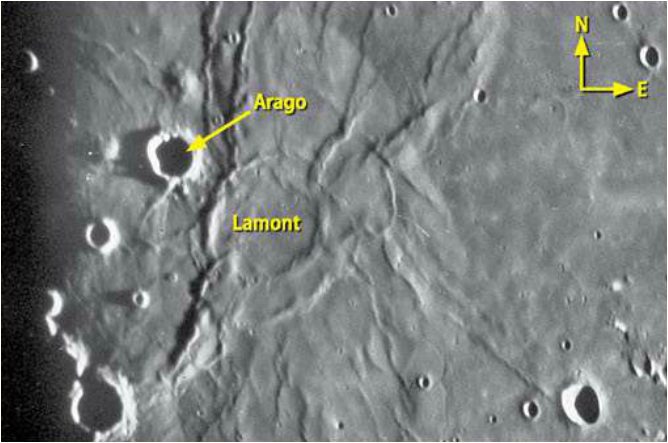
<Lamont 모습. 사진 Lunar Atlas/astronomy.com>
Lamont 이란 Crater 이름에 대해 간단히 살펴본다. 이 Crater 는 Scotland 에서 독일로 이주한 Johann von Lamont (1805~1879) 이란 천문학자 이름을 딴 것이다. 그는 지구자기 연구에 탁월한 공적이 있다고 한다. 한편 천왕성, 토성의 여러 위성 공전궤도를 계산했었고, 1845, 1846년 두 번이나 해왕성을 관측했다는데, 그것이 새로운 행성인 줄은 몰랐다고 전해진다. 해왕성 발견이 공식 인정된 때는 1846년 9월이다. 또한 같은 이름의 Lamont Carter 가 화성에도 있다. 이 분은 평생 독신으로 살았다는데, 일생을 고요히 사셨으니 고요의 바다에 제대로 안주하신 셈이다.

<50세 정도일 때의 Johann von Lamont.
사진: Journal of the Astronomical Society of Edinburgh>
(4) 위대는 평범이외다
금년 2013년은 인류가 처음 달에 착륙한 1969년으로부터 44년째 되는 해이다. 당시 저도 TV 중계를 보면서 저 곳이 진짜로 달 위가 맞나 하면서 무척 신기해 했던 기억이 있다. 그 때는 그로부터 44년 후에 제가 이런 칼럼을 쓰고 있을 줄은 아마 조물주께서만 아시고 계셨으리라. 그러면 이 칼럼 쓰고나서 또 내일부터 44년 후 저는 어디서 무얼하고 있을 지 생각해보게 된다. 기회만 된다면야 다른 차원으로 건너가서 그 곳 사람들이 뭐하고 사는지 한 번 보고 싶다.
Neil Armstrong (1930~2012) 은 1년전인 작년 2012년 8월 25일에 사망했다. 그는 성격이 조용하기도 했다지만 평생 국민영웅으로 살면서 한번도 앞에 나서서 영웅행세를 한 적 없고 겸손한 인생을 살았다고 전해진다. 사실 고난을 헤치고 목표를 성취했던 역사상 여러 인물들에 비하면 그는 국가와 수만명 과학자가 “만들어 준” 영웅임은 스스로 알고 있었을 것이다. 그렇더라도 이전에 간단히 언급드렸던 또 다른 미국 국민영웅 Charles Lindbergh (1902~1974) 의 파란 많은 인생과는 많이 대비된다.
저는 아직 배움이 짧아 어찌 사는게 도리인지 알지 못한다. 다만 Neil Armstrong 의 인생을 보면 중학교 시절, 국어 교과서엔가 나온 문구 “위대는 평범이외다” 란 말이 생각난다 (이광수, 금강산 유기 - 金剛山 遊記). 오는 8월 25일은 일요일인데 그 날엔 달을 바라보며, 비록 우리나라 사람은 아닐 지라도 항상 겸손했던 평범한 영웅 Neil Armstrong 을 생각해보려 한다.


<39세 Neil Armstrong> <사망 1년전 81세 Armstrong. usamgazine>
Astro News <끝>






 Astro News - Serial No 20 - Aug 2013
Astro News - Serial No 20 - Aug 2013
 Astro News - Serial No 18 - June 2013
Astro News - Serial No 18 - June 2013
좋은 자료 감사합니다. 기조력에 대한 자세한 설명 고맙습니다. 하늘에 있는 9마리 새를 모두 찾아봐야겠습니다.