Astro News Serial No 20. Vol No II
August 2013
<목 차>
I. Life with Kaas
탈출속도 (Escape Velocity) – 이론과 실제
(1) 탈출, 그 희망과 두려움에 대하여
(2) 지구 탈출속도 11.2 km/s 는 얼마나 빠른 속도인가
(3) 그러나 걸어서도 지구를 탈출할 수 있다
(4) 정지한 천체의 탈출속도 이론 I
– 지표면에서 수직방향으로 운동하는 경우
1. 몇 가지 가정
2. 탈출속도 개념
3. 수직운동 경우 탈출속도 공식 구하기
4. 수직운동 경우 탈출속도 수치 구하기
(5) 정지한 천체의 탈출속도 이론 II
– 지표면에서 접선방향으로 운동하는 경우
1. 네가지 운동형태
2. 접선방향 운동 경우 원운동속도 공식 구하기
3. 접선방향 운동 경우 원운동속도 수치 구하기
(6) 실제로 우주선을 발사할 경우
1. 우주선의 출발속도는 ?
2. 지구공전 인공위성들의 속도
(7) 자전하는 천체의 탈출속도
1. 적도에서의 이론상 지구탈출 속도
2. 서울에서의 이론상 지구탈출 속도
(8) 태양계 천체들의 탈출 속도
II. Not Essential But Beneficial
Schwarzschild Radius (슈바르츠실트 반지름)
(1) 전쟁터에서 연구한 수학문제
(2) Black Hole 이란 단어는 누가 만들었을까 ?
(3) 수학문제 만드는 사람, 그 문제 푸는 사람
(4) 슈바르츠실트 반지름 공식 구하기
1. 자전하지 않는 천체인 경우
2. 태양 및 행성들이 블랙홀이 될 경우의 크기 구하기
3. 자전하는 천체인 경우
III. Surprise & Mystery
새롭게 밝혀진 우리은하 모습
(1) 2005년 나선에서 막대나선으로 수정된 우리은하
(2) 직경이 하와이부터 대서양까지인 전파망원경 VLBA
(3) 삼각측량이란 ?
(4) 시차 (Parallax) 를 이용한 별까지 거리측정
1. 연주시차와 Parsec (파섹) 단위
2. 연주시차 측정경쟁 우승자 Bessel
(5) 2005~ 2012년까지 생각되던 우리은하 구조
(6) 2013년에 새로 밝혀진 우리은하 구조
(7) 아프리카 초원에서 만납시다
IV. Coffee Break
무궁화시움 (Mugunghwacium), 원소번호 119, 기호 Mm ? ?
(1) 재미있는 원소이름 – 우라늄, 플루토늄의 어원
(2) 아인슈타니움도 있다
V. Journey to Deep Sky
잃어버린 별자리를 찾아서 (8 회)
Rangifer 또는 Tarandus – 순록자리
(1) “순록” 이란 한자어에 대하여
(2) 산타클로스와 루돌프 사슴도 별자리에 있으면 좋을 듯
1. 산타클로스 출생기원
2. 루돌프 사슴 출생기원
(3) 순록이 별자리에 오르게 된 사연
1. 순록과 측지학 (Geodesy) 의 이상한 관계
2. Rangifer 와 Tarandus 의 차이
(4) 별자리 순록의 녹생여정 (鹿生旅程)
VI. Moon River Wider Than a Mile
Hyginus Crater 와 계곡
난 얻어맞고 생긴 것 아니거든 !
(1) 이열치열 – 더위는 증기사우나로 이긴다
(2) 계곡인지 도랑인지 – 히기누스 계곡
(3) 달 앞면에서 3개 밖에 없는 지형 – 히기누스 Crater
<본 문>
I. Life with Kaas
탈출속도 (Escape Velocity) – 이론과 실제
(1) 탈출, 그 희망과 두려움에 대하여
어느 노래가사를 조금 바꾸어 써 본다면, “누구나 사는 동안에 한 번 잊지 못할 탈출” 은 경험하실 것이다. 쓸쓸한 이 노래 분위기와는 달리 “탈출” 이란 단어는 대부분 좋은 의미로 인식된다. 구속과 속박, 지루한 일상 또는 사랑에서의 탈출처럼 언제나 미래에 대한 희망, 영혼의 안식 또는 신체적 자유가 탈출에 내포된 의미라고 생각한다. 우리가 탈출을 동경하고, 그것에 성공한 사람을 존경하고 부러워하는 이유는 탈출을 위한 용기와 결단, 그리고 실행이 그리 쉬운 일이 아니란 것을 잘 알기 때문일 것이다.
인간인 경우, 탈출 실행을 방해하는 요소가 미래에 대한 두려움이나 의지의 나약함이라 한다면 우주의 경우는 우리가 잘 아는 중력일 것이다. 조그만 자석의 자기력이 중력을 간단히 이겨내는 것처럼 중력은 우주에 존재하는 다른 힘들인 전자기력, 강력, 약력 등에 비해서 그리 큰 힘은 아니다. 우주생성 초기의 중력은 지금 보다 엄청 컸지만 우주가 여러 차원으로 나뉘면서 중력도 나뉘어져 현재 우리 우주의 중력이 약해졌다는 이론도 있다. 그러나 지구를 벗어나기 위해 극복해야 하는 그 중력도 인간에게는 너무도 큰 힘인 것은 사실이다.
비록 거창한 의미의 탈출은 아닐지라도 많은 분들이 지루한 일상에서 탈출하는 8 월을 맞아, 우리 지구를 비롯해서 어떤 천체를 탈출하기 위한 속도는 얼마나 되는지 알아보려 한다.
(2) 지구 탈출속도 11.2 km/s 는 얼마나 빠른 속도인가
지구 탈출속도는 11.2 km/s 라는 것은 많이 들어보셨을 것이다. 여기서의 탈출속도 (Escape Velocity)> 란 물체가 천체의 중력을 이겨내고 우주로 나가기 위해 천체표면에서 처음 출발할 때의 속도를 말한다
제가 찾아본 대부분 책이나 자료들에선 탈출속도를 설명하는데 <Rocket> 으로 설명하고 있었다. 그러나 이는 잘못된 설명이며, 읽는 분들의 혼동만 야기할 뿐이라고 생각된다. 왜냐하면 우주선이나 인공위성 Rocket 은 지속적인 추진력 때문에 천체물리학에서 말하는 탈출속도의 전제조건에 어긋난다. 더욱이 Apollo 우주선 출발속도가 11.2 km/s, 시속 40,320 km 라는 상상을 초월하는 속도였다고는 믿어지지 않기 때문이다. 이 속도가 얼마나 빠른지 감이 안오실 것 같아 빛과 소리의 속도와 비유해본다. 아래 계산에 의하면 지구 탈출속도로는 지구를 1 시간에 1 바퀴 조금 넘게 돌고 마하 34~33 이 나오는 것을 알 수 있다.
● 빛의 속도 c = 299,792,458 m/s = 초속 약 300,000 km
지구 적도 둘레 L = 40,075 km
그러므로 빛이 1 초에 지구둘레를 7바퀴 반 돈다는 계산이 나온다.
(300,000 km/s ÷ 40,075 km/L = 7.485 L/s)
지구 탈출속도 Ve = 11.2 km/s = 40,320 km/h 이므로
지구 탈출속도로는 지구를 1 시간에 1 바퀴 조금 넘게 돌 수 있다.
(40,320 km/h ÷ 40,075 km/L = 1.0006 L/h)
● 소리의 속도 S = (331.3 + 0.606 T) m/s <T 는 온도 °C>
0 °C 에선 331.3 m/s, 20 °C 상온이면 343 m/s
지구 탈출속도는 0 °C 에서의 소리 속도의 33.8 배 (약 34배) 이고
20 °C 상온이면 32.6 배 (약 33 배) 이다. 마하 (Mach) 34 및 33 이라고도 한다.
(11,200 m/s ÷ 331.3 = 33.8 배. 11,200 m/s ÷ 343 m/s = 32.6 배)
하지만 세상의 어떤 비행체라도 지표면에서 마하 33~34 로 출발하는 것은 아직 보지 못하셨을 것이다. 사실 대기권에서 이 정도 속도이면 공기와의 마찰로 비행체 금속이 견디지 못하면 유성처럼 타버릴 수도 있다. 그러나 대기가 없는 우주공간에선 당연히 가능한 속도이다. 아래에서 보시겠지만 지상 약 2,000 km 안쪽에서 지구를 공전하는 인공위성은 지구 탈출속도의 반 정도인 8.2 ~ 6.5 km/s 정도로 약 1.5~2시간 (89~128분) 에 한 번씩 지구를 돌고 있다.
탈출속도 이론에서 몇 가지 중요한 가정 중의 하나는 <출발 후에는 추진력 도움이 없다> 는 것이다. 그러나 Rocket 은 운동 중에도 계속 추진력을 내므로 당연히 탈출속도 이론을 미리 알고 계시던 분들 아니면 헷갈리실 것이다. 따라서 여기서는 지구표면에서 <수직으로 쏘는 대포> 로 설명 드리고, 또한 물체가 지표면에서 <수직> 및 <접선> 방향으로 운동하는 두가지 경우 모두 알아보겠다.
(3) 그러나 걸어서도 지구를 탈출할 수 있다
탈출속도 이론을 살펴보기 전에 한가지 짚고 넘어가려 한다. 위에서 말씀드린 탈출속도 이론의 중요한 가정인 <출발 후에는 추진력 도움이 없다>는 가정만 사라지면 탈출속도 개념이 통째로 바뀌게 된다. 만일 <출발 후에도 계속 추진력이 있으면> 아주 느린 속도로 하늘로 올라가도 지구를 탈출해서 우주로 나갈 수 있다.
프로펠러 비행기나 제트 비행기 모두 계속 추진력이 있으므로 이론상 모두 우주로 나갈 수는 있지만, 공기가 없는 우주공간에선 추진력을 낼 수 없다. 따라서 지구 대기권 밖에선 무용지물이므로 다른 예를 들어본다. 만일 계단을 지구 바깥 우주까지 설치한다면 천천히 걸어서 우주로 나갈 수 있을까 ? 물론 상상하신 것처럼 우주로 나갈 수 있다. 몇 년 전에 우주까지 뻗는 엘리베이터를 설치해서 달까지 쉽게 여행하자는 아이디어을 본 기억이 있다. 걷는 것이나 엘리베이터나 모두 11.2 km/s 보다 속도가 턱없이 느리지만 당연히 지구를 탈출할 수 있다.
우주선 Rocket 속도가 어느 정도 빠른 이유는 지구 공전궤도를 돌 수 있는 속도를 맞추기 위한 것 또는 달 같은 목적지까지 빨리 도달하기 위함도 있다. 요점은 만일 출발 후에도 계속 추진력이 있으면 <천천히 가도 지구를 탈출할 수 있다> 는 것이다. 다만 천천히 가더라도 당연히 물체의 중량을 지속적으로 하늘로 올리기 위한 힘은 필요할 것이다.
(4) 정지한 천체의 탈출속도 이론 I
– 지표면에서 수직방향으로 운동하는 경우
1. 몇 가지 가정
먼저 자전 운동하지 않고 정지해 있는 천체의 탈출속도를 알아보겠다. 지표면에서 수직방향이란 지구 중심과 물체를 연결하는 선 방향으로 물체가 운동함을 의미한다. 우선 아래 그림부터 보시지요.
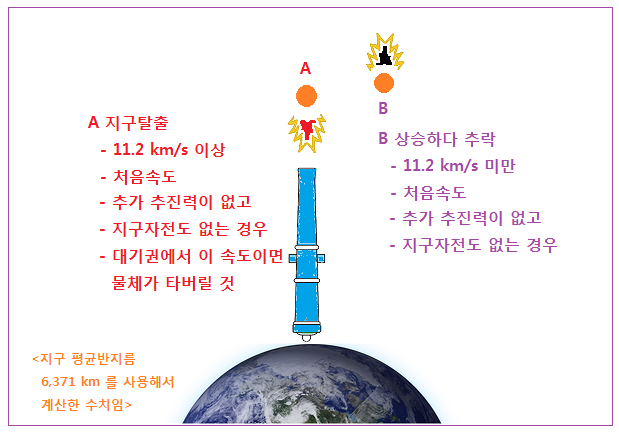
<지표면에서 수직으로 대포를 쏘는 경우>
일단 지구 탈출속도는 11.2 km/s 라고 임을 알고 계시고, 대포알이 이 속도 이상으로 쏘아지면 지구를 벗어나 우주로 계속 나아가지만 이 속도 미만일 경우, 어느 정도까지는 올라가다가 결국 지구 중력에 붙들려 다시 추락함을 나타낸다. 실제 우주선 Rocket 을 발사할 때는 Rocket 에 계속 추진력을 줄 수 있으므로 11.2 km/s 로 발사하는 것은 아니고 다른 방법을 사용한다. 실제 우주선 Rocket 경우에 대해선 이 칼럼 후반부에서 설명 드리겠다.
하여간 탈출속도를 구하는 계산에는 아래와 같은 중요한 전제조건 (가정) 이 있다.
가정 1 : 천체가 <정지한 상태> 이며 자전이나 공전 같은 회전운동은 하지 않는다.
가정 2 : 물체가 운동을 시작하는 <최초의 추진력> 이외에 운동중간의 다른 추진력은 없다.
가정 3 : 물체가 운동을 시작하는 위치는 천체의 <표면> 이다.
가정 4 : 지구 탈출속도 보다 큰 경우에 물체는 우주공간 <무한한 거리> 로 중간에
정지하지 않고 무한한 시간 동안 상승한다.
가정 5 : <지구중력만 작용> 하며 대기마찰 같은 다른 변수 영향은 없다
지구 탈출속도를 구할 때는 위의 가정을 전제로 하고 <에너지 보존법칙> 을 이용해서 계산한다.
이 법칙에 따르면 물체가 운동할 때 <위치에너지> 와 <운동에너지는> 서로 교환되면서 그 합계는 일정하게 보존된다. 에너지 보존법칙에 따른 지구 탈출속도 정의는 아래와 같다.
2. 탈출속도 개념
아래 설명은 지구를 기준으로 물체가 지표면에서 수직으로 상승하는 경우를 기준으로 설명 드리겠다. 물론 설명은 지구를 기준으로 한 수직 운동이지만 모든 천체와 모든 방향에 적용될 수 있다. 우선 정의에 대한 개념을 먼저 설명 드리고 그 다음에 수식으로 풀어 드린다.
a) 물체가 우주공간 <무한대 (∞) 거리> 로 이동할 수 있는 <출발 속도>.
● 물체가 지표면을 떠나서 우주공간 무한히 먼 거리로 이동함을 의미한다.
무한히 먼 거리는 수학에서 <무한대 (∞) 거리> 라고 말한다.
이 무한대 개념이 탈출속도 정의에서 가장 중요한 부분이다.
● 출발속도는 물체가 처음 운동을 시작하는 순간의 속도를 말한다.
b) 물체가 무한대 (∞) 거리로 이동하면 <지구중력은 0> .
● <중력> 은 영어로 Gravitation 또는 Gravity 로서 여기서는 약자 <Fg> 로 쓴다.
정의는 아래와 같다.
중력 (인력) Fg = GmM / r ² G 중력상수 (Serial No 10 참조)
6.67384 x 10−11 m3 kg -1 sec -2
m 물체 질량 (kg)
M 지구 질량 (kg)
r 지구중심에서 물체중심까지 거리 (km)
● 물체가 무한히 먼 거리인 무한대 (∞) 거리까지 가면 지구중심에서 물체중심까지 거리인
( r ) 이 무한대 (∞) 가 되므로
무한대 (∞) 거리에선 Fg = 0 이다
물론 지구 중력이 미치는 범위는 한정이 되어 있으나 중력의 수학적 의미라고 생각
하시면 된다.
c) 물체가 무한대 (∞) 거리로 이동하면 <운동에너지도 0 >.
● <운동에너지> 는 영어로 Kinetic Energy 라 하며, 여기서는 약자로 <Ek> 라고 쓰겠다.
정의는 아래와 같다.
운동에너지 Ek = m V ² / 2 m : 물체 질량 (kg)
V : 물체의 운동속도 (km/s)
● 위의 그림에서 대포알이 지구 탈출속도보다 작다면 상승하면서 속도가 점차
감소하다가 맨 꼭대기에서 어느 순간 잠시 멈추고 다시 추락하는 것을 추정할 수 있다.
여기서 잠시 멈춘다는 것은 그 순간의 속도는 ( 0 ) 임을 의미한다.
속도 V가 ( 0 ) 이면 위의 공식에 의해서 운동에너지가 ( 0 ) 가 된다.
● 반면에 대포알이 지구 탈출속도보다 크더라도 우주공간 무한히 먼 곳까지는 이동하지만
이동 중에 속도는 줄어들 것이고 무한히 먼 거리까지 가면 속도가 ( 0 ) 에 <수렴>
한다.
● 물론 탈출속도보다 큰 경우 위의 가정 4 처럼 상승하다가 정지하지는 않는 것이
전제조건이지만 무한히 먼 거리에선 속도가 ( 0 ) 에 <수렴> 하다가 무한대 (∞)
거리에선 속도가 수학적으로 ( 0 ) 이다. 속도 V가 ( 0 ) 이므로 위의 운동에너지
공식에 따라 운동에너지도 ( 0 ) 가 된다.
● 따라서 무한대 (∞) 거리에선 Ek = 0 이다.
d) 물체가 무한대 (∞) 거리로 이동하면 <중력 위치에너지도 0 >.
● 에너지 보존법칙으로 표현하면 물체가 이동하는 중에 다른 별도의 추진력은 없기
때문에 <물체의 운동 에너지가 모두 위치에너지로 바뀐다> 고 할 수 있다.
● 위치에너지에는 중력 (인력), 탄성력, 전기력, 강력, 약력, 분자간 위치에너지 등 여러
종류가 있다. 탈출속도 개념에 사용되는 것은 <중력 위치에너지> 이다.
● <중력 위치에너지>는 운동에너지와 달리 <어떤 기준점을 필요에 따라 정하고>
물체가 그 기준점 보다 중력을 더 많이 받는 <높은 위치>에 있으면 < + 값> 을
갖는 것으로 정하고, 중력을 더 적게 받는 <낮은 위치>에 있으면 < - 값> 을 갖는
것으로 정했다.
만일 지표면 1 m 상공을 기준점이면, 1 m 위의 중력 위치에너지는 < + 플러스 값>
이고, 기준점인 정확한 1 m 상공은 < 0 > 이며 바로 그 아래는 < - 마이너스 값>
으로 정의해 놓은 것이다. 따라서 어떤 지점을 기준으로 정하느냐에 따라서 중력
위치에너지 수치는 달라지게 된다. .
● 그런데 <물리학>에서 사용하는 관습은 어떤 천체의 표면에서 <무한대 (∞) 거리>
상공의 지점을 <중력 위치에너지 기준점> 으로 정하고 사용한다. 따라서 무한대 (∞)
상공의 중력 위치에너지는 ( 0 ) 이고 그 아래는 모두 ( - 마이너스) 가 된다. 무한대 (∞)
상공의 “위” 라는 수학적 개념은 없으므로 당연히 중력 위치에너지에서 < + 플러스 값>
은 존재할 수 없다.
이를 달리 설명하면 다음과 같다. 상식적으로 생각해서 지구중심 ( r ) 에서부터
무한대 (∞) 까지 물체를 위로 끌고 가려면 지구 중력을 이겨내는 플러스 ( + ) 의
힘이 필요하다. 그러나 물리학에서 정한 중력 위치에너지 기준점은 무한대 (∞) 거리에
있으므로 중력 위치에너지는 <그 무한대 (∞) 기준점으로부터 지구의 어떤 지점까지
물체를 아래로 끌고 오는 힘> 이다. 그런데 지구까지 아래로 끌고 오는 데는 지구
중력이 일을 해 주므로 무한대 위로 끌고 올라갈 때 드는 ( + ) 힘의 반대인 ( - ) 의
힘이 든다는 개념이다.
하여간 물리학에서 그렇게 정해놓고 쓰므로 크게 괘념치 않으셔도 될 듯하다.
● <중력 위치에너지>는 영어로 Gravitational Potential Energy 라고 하며, 여기서는
약자로 <Ep> 라고 쓰겠다. 정의는 아래와 같다. 지구를 예로 설명 드린다.
중력 위치에너지 Ep = - (마이너스) GmM / r
G 중력상수 (Serial No 10 참조)
6.67384 x 10−11 m3 kg -1 sec -2
m 물체 질량 (kg)
M 지구 질량 (kg)
r 지구중심에서 물체중심까지 거리 (km)
대포알이 지구 탈출속도보다 크다면 지표면을 떠나 우주공간 무한히 먼 곳까지 이동해서
무한대 (∞) 거리까지 간다는 가정이므로 지구중심으로부터 거리 ( r ) 도 무한대 (∞) 가
된다. 중력 위치에너지 공식에서 ( r ) 이 무한대 (∞) 이면, 중력 위치에너지 값은
- (마이너스) 0 이며 이는 ( 0 ) 과 같다.
정리하면, 무한대 (∞) 거리에선 Ep = 0 이다.
e) 따라서 탈출속도란 <물체가 무한대 (∞) 거리로 이동해서 중력이 0 이 되고 운동에너지도
0 이 되며, 중력 위치에너지 또한 0 이 될 수 있는 처음속도> 를 말한다.
f) 기타 보충사항
● 위의 탈출속도 V 는 천체중심에서 수직방향이든 접선방향이든 또는 비스듬한 각도이든
<모든 방향으로 적용> 되는 개념이다.
● 물리학에서 속도 (Velocity) 는 <방향> 이 있는 Vector (벡터량) 이지만,
탈출속도 (Escape Velocity) 개념에서 속도는 어느 방향이든 적용되므로 방향성이 없는
<Scalar (스칼라량)> 이다. 따라서 탈출속력 (Escape Speed) 가 더 적절한 용어이지만,
여기서는 관례대로 탈출속도 (Escape Velocity) 라고 사용했다.
위의 개념설명을 이해하시기 쉽도록 그림으로 그려 보았다. 글자가 많으나 살펴보고 지나가시기 바랍니다.
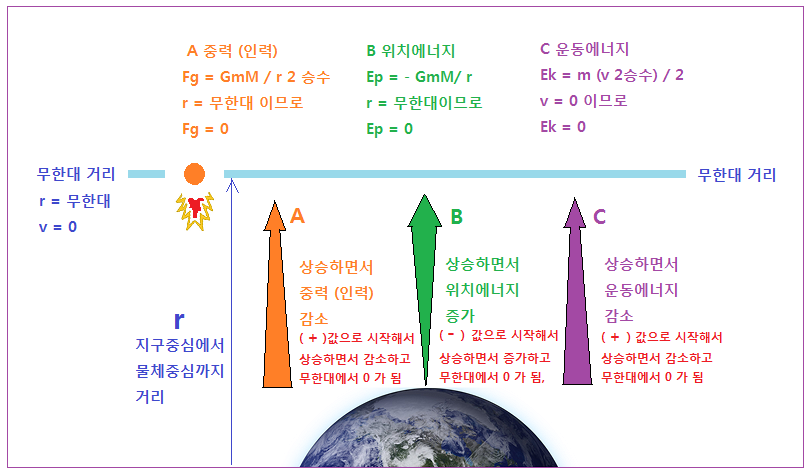
<탈출속도 개념>
3. 수직운동 경우 탈출속도 공식 구하기
위에서 말씀드린 운동에너지 Ek = m V ² / 2 이고
중력 위치에너지 Ep = - (마이너스) GmM / r 임을 기억하시면 됩니다.
다만 운동에너지와 중력 위치에너지 공식이 도출되는 과정은 저의 한계를 넘으므로 생략합니다.
1. 에너지 보존법칙
처음 (운동에너지+중력 위치에너지) = 나중 (운동에너지+중력 위치에너지)
이를 위의 용어 사용해서 수식으로 표현하면,
Start [ Ek + Ep ] = Final [ Ek + Ep ] ------ ⓐ
2. 공식에 따르면
운동에너지 Ek = m V ² / 2 ------ ⓑ
중력 위치에너지 Ep = - (마이너스) GmM / r ------ ⓒ
3. 만일 아주 먼 거리이면 속도는 점점 0 에 가까워져서 <무한대 거리에선 속도는 0 >
이다. Final (Ek) = Final (m V ² / 2) 에서 Final V = 0 이므로
Final (Ek) = 0 ----- ⓓ
또한 <무한대 거리에선 r = 무한대> 이므로 Final ( - GmM / r ) = 0 이 된다.
따라서
Final (Ep) = 0 ----- ⓔ
4. 위의 ⓐ 식에 ⓓ ⓔ 를 대입하면
Start [ Ek + Ep ] = 0 + 0 이며 여기에 ⓑ ⓒ 를 대입하면
Start [ (m V ² / 2) + ( - GmM / r ) ] = 0 + 0 = 0 ----- ⓕ
5. ⓕ 식을 정리하면
m V ² - GmM
Start [ -------- + ---------- ] = 0 이고, 통분해서 m 을 소거하면
2 r
Start V² = Start [ 2 GM / r ]
탈출속도는 당연히 처음의 속도 (Start) 이므로 Start 를 빼고 정리하면,
V = (2 GM / r ) 1/2 ----- ⓖ 또는
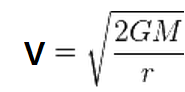
따라서 탈출속도 V 는 오직 천체의 질량 M 과 천체중심과 물체중심 사이의 거리 r 에만
관련이 있음을 알 수 있다.
4. 수직운동 경우 탈출속도 수치 구하기
그러면 우리가 알고 있는 지구 탈출속도 11.2 km /s 가 맞는지 위 공식으로 한 번 검증해본다.
필요한 수치는,
G 중력상수 : 6.67384 x 10−11 m3 kg -1 sec -2
M 지구질량 : 5.9736 x 10 24
r 지구중심에서 물체중심까지 거리 :
물체가 작고, 지구표면에 있다는 가정이므로 지구반지름과 같다.
지구평균 반지름 6,371 km
위 수치를 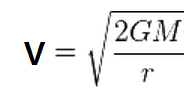
V = (0.01252 km 2 sec - 2 ) 1/2
= 11.18928 km/sec 이다.
따라서 대략 11.2 km /s 라고 할 수 있다.
참고로 지구 반지름은 극지방과 적도지방이 다르므로 지구 반지름 수치를 어떤 것을 사용하는가에 따라 수치에 조금씩 차이가 날 것이다. 위의 수치는 지구적도 반지름이 아니고 지구의 평균반지름 (Mean Radius) 인 6,371 km 를 사용한 수치임에 유의하십시오.
(5) 정지한 천체의 탈출속도 이론 II
– 지표면에서 접선방향으로 운동하는 경우
1. 네가지 운동형태
위의 탈출속도를 구하는 과정에선 지표면에서 수직으로 운동하는 경우만 예를 들어 설명 드렸다. 이 경우에는 탈출속도가 넘으면 우주로 나가던가, 그 속도에 못 미치면 수직으로 올라가다가 결국 추락하는 두 가지 방법 밖에 없다.
그러면 지표면과 비스듬하거나 또는 접선 방향으로 출발하면 어떤 결과가 나올까 ? 위에서 설명드린 것처럼 탈출속도 V 는 천체중심에서 모든 방향으로 운동하는 물체에 적용되는 개념이지만, 비스듬한 각도로 출발할 경우의 물체 운동궤적은 수직으로 올라가는 경우의 두가지 보다는 다양한 형태를 보인다.
여기에서 언급 드리는 사항의 기본 개념은 Issac Newton 의 1728 년 발표 논문인 <A Treatise of the System of the World> 에 나오는 내용이라고 한다. 참고로 그의 유명한 저서 <Principia> 가 발행된 년도는 1687 년이다.
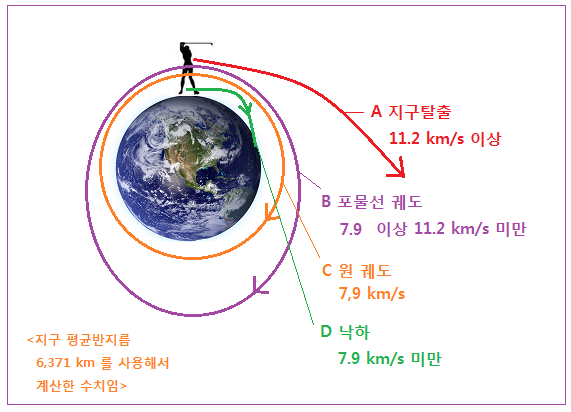
<지표면에서 접선방향일 경우의 운동궤적>
A 지구탈출
이는 잘 아시는 11.2 km/s 이다. 처음 골프 공을 타격했을 때 이 속도가 나오면 지구를
영원히 떠나는 골프공이 될 것이다.
B 포물선 궤도 운동
11.2 km/s 보다 작고 7.9 km/s 보다 조금이라도 크면 지구에서 멀리 떠나는 듯 하다가
다시 지구 중력에 이끌려 돌아오게 되며 포물선 궤도로 지구를 영원히 공전할 것이다.
C 원 궤도 운동
7.9 km/s 이면 C 처럼 원 궤도로 지구를 공전한다. 이 숫자가 도출되는 과정은 바로
아래 단락에서 설명 드린다.
7.9 km/s 는 지구 “표면” 을 원 궤도로 공전하는 속도이다.
공전주기를 구하려면 지구 평균원주 ÷ 7.9 km/s 하면 된다. 지구 평균 반지름
(Mean Radius) 은 6,371 km 이므로, 2 x π (3.14) x 6,371 km/7.9 km/s = 5,064.54 초
= 84.40 분 = 약 85 분이 된다.
그림은 지구에서 조금 떠 있으나 7.9 km/s 라는 속도는 지표면이 전제조건이다.
만일 인공위성처럼 지표면에서 일정거리 떠 있는 물체인 경우는 아래 단락에서 도출하는
공식에서 지구 중심에서의 거리 ( r ) 만 바꾸어 주면 된다.
D 낙하
7.9 km/s 보다 조금이라도 작은 경우로서, 신나게 멀리 가더라고 결국 땅으로 떨어지는
것을 표시한다.
2. 접선방향 운동 경우 원운동속도 공식 구하기
돌멩이에 끈을 달고 회전시키는 경우, 돌멩이가 등속도 원운동 하려면 원심력과 구심력이 같아야 한다. 여기서의 구심력은 끈이 돌멩이를 잡아당기는 함이다. 같은 이치로 지구표면을 떠난 물체가 지구표면 위에서 등속도 원운동 하려면 원운동에 따른 원심력과 구심력이 같아야 하는데, 여기서의 구심력은 지구 중력이 될 것이다.
이 칼럼에서 몇 차례 언급드린 원심력과 중력의 공식과 추가로 선속도 공식은 아래와 같다.
원심력 (Fc) Fc=m r ω2 - m : 물체의 질량.
- r : 물체가 원운동 할 때 반지름 = 지구반지름
- ω : 물체가 원운동 할 때 각속도
중력 (Fg) Fg = G mM / r ² - G : 중력상수 (Serial No 10 참조)
6.67384 x 10−11 N m2 / kg 2 또는
6.67384 x 10−11 m3 kg -1 sec -2
- m : 물체의 질량.
- M : 지구의 질량.
- r : 물체가 원운동 할 때 반지름 = 지구반지름
선속도 (V) V = r x ω - r : 물체가 원운동 할 때 반지름 = 지구반지름
- ω : 물체가 원운동 할 때 각속도
1. 물체가 등속도 원운동 하려면 원심력 = 구심력 (지구중력) 이므로,
Fc= Fg 에서
m r ω2 = G m M / r ²
양변에서 m 을 소거하고 r 을 우변으로 이항하면
ω2 = G M / r ³ -------------- ⓐ
2. 한편 선속도 (V) V = r x ω 이므로 ω = V / r --------- ⓑ
ⓑ 를 ⓐ 에 대입하면 V ² / r ² = G M / r ³
양변에서 r ² 를 소거하면
V ² = G M / r --------------- ⓒ
3. ⓒ 식을 정리하면
V = ( GM / r ) 1/2 또는
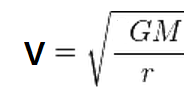
위 식을 수직 운동하는 물체의 탈출속도인 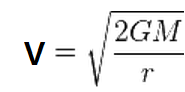
<루트 2> 만큼 적은 수치임을 알 수 있다.
3. 접선방향 운동 경우 원운동속도 수치 구하기
그러면 지구표면에서 원운동하는 경우 처음 출발속도를 구해본다.
모든 변수들을 입력할 수도 있지만 이미 위에서 수직운동하는 경우의 탈출속도를 구했으므로
그 수치를 <루트 2> 를 나누면 될 것이다.
따라서 11.18928 km/s ÷ 루트 2 (약 1.414213)
= 7.9120 km/s
= 약 7.9 km/s
만일 지구표면에서 하늘 높이 떠있는 인공위성이 지구 궤도를 원 운동하기 위한 속도는
( r ) 이 커지므로 7.9 km/s 보다 작아짐을 알 수 있다.
한편 수직방향 운동에서도 언급 드린 것과 같이 위의 수치는 지구적도 반지름이 아니고 지구의 평균반지름 (Mean Radius) 인 6,371 km 를 사용한 수치임에 유의하십시오.
(6) 실제로 우주선을 발사할 경우
1. 우주선의 출발속도는 ?
그런데 우주선이 발사되는 장면 기억해보시면 절대로 탈출속도는 아님을 아실 것이다.
11.2 km/s 속도는 시속 40,320 km 라는 엄청난 속도인데, 우주선이 발사될 때 이런 속도가 된다고는 절대로 생각되지 않으실 것이다. 11.2 km/s 라는 속도는 위에서 강조 드린, “지구가 정지해 있고, 중간의 추진력이 없다” 는 전제조건이 있어야 한다. 우주선은 당연히 로켓에서 계속 추진력이 나오므로 <최초의 속도가 11.2 km/s 일 필요는 없다>.
우주왕복선 (Space Shuttle) 의 양쪽에 달린 Booster 는 고체연료 (Solid Fuel) 을 사용하는데 이것은 추진력은 평균 7 km/s 정도라고 한다. 한편 Apollo 우주선들에 사용된 Saturn-V 로켓은 액체수소 (LH2 – Liquid Hydrogen) 와 액체산소 (LOX – Liquid Oxygen) 를 사용했는데, 이것은 평균
9 km/s 정도만 가능하다.


<우주왕복선 Booster –고체연료 7 km/s> <Saturn-V 로켓 액체연료 9 km/s>
실제로 로켓 엔진을 만들 때 지구탈출 속도인 11.2 km/s 를 내도록 제작하는 것은 비용만 많이 들 뿐 필요하지도 않고 대기권과의 마찰로 우주선이 불타버릴 것이다. 따라서 우주선을 발사할 때는 지상 2,000 km 정도까지만 우주선을 천천히 올려 놓고 그 곳에서부터 추진력을 좀 더 세게 해서 8 km/s 정도로 유지하면서 우주로 진입한다.
2. 지구공전 인공위성들의 속도
지표면 바로 위에서 2,000 km 상공까지를 LEO (Low Earth Orbit) 라고 한다. 아래 그림에서 푸른색으로 표시한 부분이 LEO 이며 우주선은 약 2,000 km 상공에서 추진력을 가속해서 우주로 진출한다. 그림에서 허블망원경은 지상 595 km 궤도에 머무는 것이 표시되어 있다.
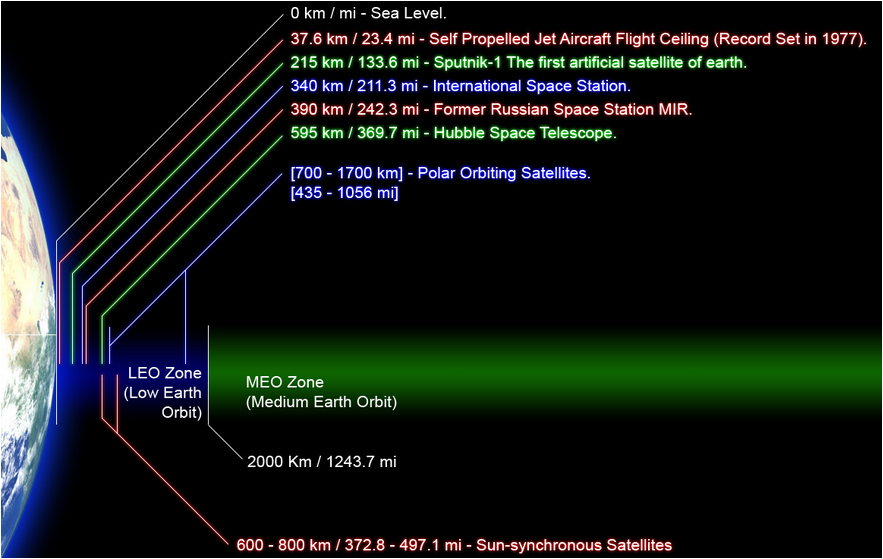
<Low Earth Orbit – 지상에서 2,000 km 까지 상공>
위 그림에서 보이는 LEO (Low Earth Orbit) 지역에 있는 지구공전 위성들의 속도를 찾아보았다.
원 궤도로 공전하는 위성의 속도는 7.8 ~6.9 km /s 이고
타원 궤도로 공전하는 위성의 속도는 8.2 ~ 6.5 km/s 이며
공전궤도 주기는 89 ~ 128 분 이라고 한다.
(7) 자전하는 천체의 탈출속도
1. 적도에서의 이론상 지구탈출 속도
사소한 부분이지만 우주선 발사기지는 대부분 적도에 가까운 곳으로 한다. 이는 적도에서 최대인 지구 자전속도의 도움을 받으려는 시도이다. 우주선도 지구 자전 도움을 받지만 추진력 때문에 예를 들기 적합하지 않으므로 대포알을 예로 든다. 지구는 서쪽에서 동쪽으로 자전하므로 대포를 적도에서 동쪽으로 접선방향으로 발사하면 지구 자전속도 만큼 도움 받을 것이다.
그러면 적도에서의 지구 자전속도는 얼마나 될까 ? 여기서 자전속도는 당연히 선속도 (Linear Velocity) 를 말한다. 필요한 수치와 계산결과는 아래와 같다.
지구 적도둘레 40,075. 017 km
지구 자전주기 86,400 초 (24 시간)
40,075. 017 km ÷ 86,400 초 = 0.46383 km/s = 463.83 m/s
따라서 적도에서 지구자전 방향인 동쪽으로의 지구 탈출속도는 이론상
11.2 km – 0.46383 km/s = 10.7361 km/s 이다.
이 말은 적도에서 대포를 지표면 접선방향으로 동쪽으로 발사하면 지구 탈출속도 대비 4.14 % 만큼 속도를 업고 가게 된다. 도움을 받는 건 우주선 경우도 마찬가지이다. 몰론 지구자전 반대 방향인 서쪽으로 발사하면 463.83 m/s 만큼 손해를 보게 된다.
2. 서울에서의 이론상 지구탈출 속도
그러면 우리나라 서울에서 대포를 발사하거나 우주선 발사기지가 있다면 어느 정도 도움을 받을 수 있는지 계산해 보겠다. 이 사항은 꼭 지구 경우뿐만 아니라 모든 천체의 위도 변화에 따른 선속도 변화에 적용되므로 기억해 두실만하다. Serial No 5 에 올려드린 사항에 일부 추가해서 다시 말씀 드린다. 아래 그림 보시지요.
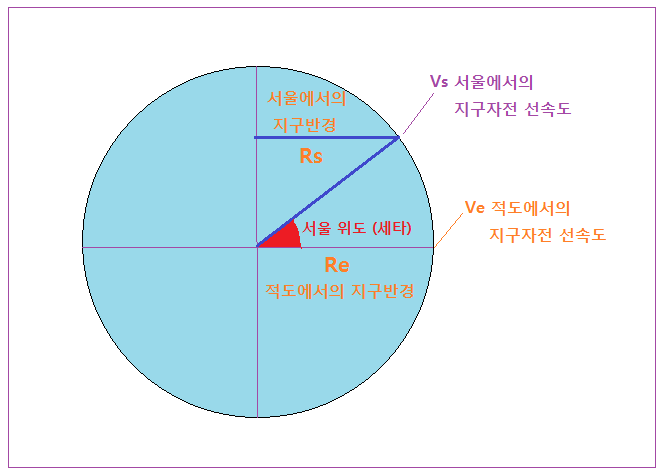
<위도 변화에 따른 선속도 변화>
위 그림에 사용된 기호들 의미는 다음과 같다.
Vs 서울에서의 지구자전 선속도
θ 서울의 위도 37.5 °
Ve 적도에서의 지구자전 선속도
Re 적도에서의 지구 반경
Rs 서울에서 지구 자전축까지 거리 (그림 참조)
ω 지구자전 각속도 (360 ° ÷ 24 시간 = 15 °/ h 로 일정함)
여기서 Vs 를 구하면 된다. 우선 선속도와 각속도 관계를 보면,
Vs = Rs x ω 이고 ----- ⓐ
Ve = Re x ω = 0.46383 km/s 이다. ----- ⓑ
한편 Cosine θ = Rs / Re 이므로 Rs = Cosine θ x Re ----- ⓒ
ⓐ 식에 ⓒ 식을 대입하면
Vs = Cosine θ x Re x ω ----- ⓓ
그런데 ⓑ 식에서 Re x ω = Ve 이므로 ⓐ 에 ⓓ 를 대입하면
Vs = Cosine θ x Ve
= Cosine 37.5 ° x 0.46383 km/s
= 0.793353 x 0.46383 km/s
(코사인 값은 코사인표 또는 공학용계산기 이용)
= 0.36798 km/s = 367.98 m/s
위 식에서 보시듯이 천체 어떤 지점의 선속도는 그 천체 적도에서의 선속도 수치에 그 지점 위도의 Cosine 값을 곱하면 된다. 위도 37.5 ° 인 서울의 지구자전 선속도는 Cosine 37.5 ° 값이
0.793353 이므로 적도에서의 지구자전 선속도에 비해 79.63 % 이다.
따라서 서울에서 지구자전 방향인 동쪽으로 대포를 발사하면 대포알의 지구 탈출속도는 이론상
11.2 km – 0.36798 km/s = 10.83202 km/s 이다.
이는 적도에서의 지구탈출 속도보다 0.09592 km/s, 95 m/s 차이이므로 그리 적은 편은 아니다. 대포가 아닌 우주선도 서울에서 발사할 경우에 적도지방에 비해 그리 나쁜 조건은 아닌 것 같다. 그러나 지구자전 반대 방향인 서쪽으로 발사하면 367.98 m/s 만큼 연료 손해를 볼 것이다.
(8) 태양계 천체들의 탈출 속도
참고 삼아 태양계 행성의 탈출속도를 정리한 표를 올려드리므로 일견해 보십시오. 해당천체 표면에서 해당천체를 탈출하는 경우와 표면에서 태양계를 탈출하는 두가지 경우이다. 숫자는 위에서 설명드린 정지한 천체의 표면을 탈출하는 경우의 모든 전제조건이 그대로 적용된다.
천 체 표면에서 해당천체 탈출 표면에서 태양계 탈출 아래 참고
-------------------------------------------------------------------------------------
태 양 617.5~617.7 km/s - (a)
수 성 4.3 67.7
금 성 10.3 49.5
지 구 11.2 42.1 (b)
달 2.4 42.1 (c)
화 성 5.0 34.1
목 성 59.5 18.5
토 성 35.6 13.6
천왕성 21.2 9.6
해왕성 23.6 7.7
태양계 내부에서 우리은하 탈출 : 525 km/s
-----------------------------------------------------------------------------------------
( - ) 표시는 자료를 구하지 못한 항목이다.
(a) 태양
617.5~617.7 km/s 는 자료에 따라 수치가 다름을 표시했다. 태양은 규모가 크므로
적용하는 변수에 따라 수치 차이가 많을 것이다.
(b) 지구
태양계를 탈출하려면 태양 자체뿐만 아니라 다른 행성들의 중력도 감안해야 한다.
태양계에서 태양질량은 98 % 이며 나머지 행성들이 2 % 를 차지한다. 42.1 km/s 는
다른 행성들의 중력도 감안된 수치이다.
(c) 지구와 달
지구와 달 사이 거리 및 달의 질량은 태양으로부터 거리 및 태양 질량에 비해 무시해도
좋을 만큼 작으므로 지구와 같은 수치로 표시했다.
위의 표에서 태양계 내부로부터 어떤 물체가 우리은하를 탈출할 수 있는 속도도 같이 표시해 드렸다. 525 km/s 는 시속 189만 km 라는 상상이 잘 안되는 속도이다. 그러나 위에서 이미 말씀 드린대로 지속적 추진력만 있다면 완행열차 타고도 우리은하를 벗어나 우주 어디든 갈 수 있다.
다만 시간이 문제인데, 빛의 속도로 움직여도 태양과 가장 가까운 항성인 Proxima Centauri 까지 가는데 4.22~4.24 년이 걸린다. 하물며 생물이 거주할 만한 다른 가까운 행성까지 거리야 수천, 수만 광년 이상이므로 더 말할 것도 없다. UFO 를 믿지 않는 사람들의 논리 중의 하나가 바로 우주여행의 걸림돌인 행성간 이동에 따른 시간의 문제이다. 따라서 요즘 영화들을 보면 반드시 지구 궤도 부근에 설치된 Worm Hole (웜홀) 을 통과해서 우주여행 하는 것으로 되어있다.
그러나 우리 우주에는 지구인이 아직 알지 못하는 물리학 체계가 있을 지도 모른다. 예를 들면 중력파를 추진력으로 이용하는 방법도 있을 수 있고…. 아니면 초끈이론 (Superstring Theory) 개념처럼 여러 차원으로 구성된 우주에서 UFO 가 다른 차원에서 건너왔을 수도 있다. 또한 다중우주 이론처럼 다른 우주와 우리 우주의 접합부분을 통과해서 UFO 가 여행할 수도 있다. 하여간 우리가 지금 증명하지 못한다고 해서 새로운 물리학이 존재하지 않는다고 부정할 수는 없을 것이다.
II. Not Essential But Beneficial
Schwarzschild Radius (슈바르츠실트 반지름)
(1) 전쟁터에서 연구한 수학문제
<슈바르츠실트 반지름>은 영어로 <Schwarzschild Radius> 라고 쓰는데, 이는 <Karl Schwarzschild (1873~1916)> 라는 독일 물리학자가 연구한 것이다. 이름을 독일어 철자로 쓰면 좀 복잡해 보이므로 아래에선 우리말 발음 그대로 “슈바르츠실트” 라고 쓰겠다.
그런데 여기서 위에 써드린 이 분의 출생과 돌아가신 연도를 자세히 보시기 바란다. 1873년 출생에 1916년 사망이므로 43세에 돌아가신 것이 된다. 이 분이 <슈바르츠실트 반지름> 및 이와 관련된 몇 가지 이론을 창안한 때는 사망하던 해인 1916년으로, 아인슈타인이 1915년에 발표한
다음해이다.
이 분은 독일계 유태인으로서 Frankfurt 에서 출생해서 Vienna 의 Kuffner 천문대를 거쳐 독일 Göttingen 대학교 교수 및 Potsdam 연구소에서 근무했다. 여기까지는 다른 학자들과 크게 다를 바 없다. 그러나 1914년 1차 세계대전이 일어나자 41세의 나이에도 불구하고 독일 포병 장교로 참전한다. 다른 학자들 같으면 참전요청을 받아도 나이와 직업을 핑계로 기피하겠지만, 전쟁의 옳고 그름을 논의 대상에서 제외한다면, 중년 나이에도 불구하고 기꺼이 참전한 용기가 존경스럽다. 그러나 이 참전은 결국 그의 수명을 단축하는 결과가 되었다.
참전 다음해인 1915년, 42세 나이에 러시아 전선 근무 중 피부에 수포가 생기는 병을 얻어 고생한다. 그러나 같은 해에 아인슈타인이 상대성 이론을 발표하자 피부병 치료중임에도 불구하고 1915년부터 1916년 까지 1년여 동안 상대성 이론에 관련된 2편의 논문과 양자역학 논문 1 편을 완성했다. 이 논문 중 하나가 아인슈타인 중력장 방정식의 해답인데, 이것이 <슈바르츠실트의 함수 또는 계량 (Schwarzschild Metric) > 이라 부르는 것이다.

<Karl Schwarzschild (1873~1916) 사진 faculty.etsu.edu>
군인 신분이 아님에도 불구하고 중년의 나이에 용감히 참전한 것도 존경스럽지만, 전선에서 피부병으로 고생하면서도 당시 발표된 아인슈타인의 최신 연구성과를 토대로 논문을 집필한 그의 열정이 더욱 존경스럽다. 그러나 그의 운은 거기까지였는지, 다음 해인 43세에 결국 피부병 때문에 사망했다.
헌데 그에게는 Martin Schwarzschild 라는 물리학자 아들이 있었는데, 이 사람은 Hitler 가 집권하자 발 빠르게 총알같이 미국으로 망명해서 Princeton 대학교 교수가 되었다. 우직하고 용감했던 그의 아버지 행적과는 너무도 비교된다. 그러나 어차피 Hitler 치하에서 유태인 신분으로는 생명조차 유지하기 어려웠을 것이므로 정세 판단은 잘한 일이라 생각된다.
(2) Black Hole 이란 단어는 누가 만들었을까 ?
슈바르츠실트 반지름을 소재로 정한 후에 서점에 들러서 천문학, 물리학 교양서적을 뒤져보고 인터넷 자료들도 훑어 보았었다. 저의 전공은 천문학, 물리학과는 거리가 멀기 때문에 안타깝게도 전문서적에 대한 접근은 능력 밖이다.
제가 접근 가능한 자료들에선 <반지름 공식> 도출과정에 대한 설명은 없이 개념만 간단히 언급하거나, 수식이 있더라도 반지름 공식을 응용한 수식들을 나열하고 있었고, 애초에 그가 공식을 유도하기 시작한 <근거>에 대해 언급한 것은 찾을 수 없었다. 따라서 여러 자료를 읽어보고 당시의 물리학계 상황을 추정해서 제 나름대로 슈바르츠실트 반지름 공식이 나오게 된 근거를 추정해 보았다. 제가 잘못 이해한 부분에 대해 지적해 주시면 감사 드리겠습니다.
슈바르츠실트 반지름을 설명하는 대부분 자료를 보면 <어떤 천체가 블랙홀이 되기 위한 반지름> 이라고 되어 있다. 물론 틀린 말은 아니지만 슈바르츠실트가 이 개념을 창안하던 1916년에 과연 <블랙홀> 이란 개념이 있었을까 ? 블랙홀은 <중력장 (Gravitational Field)> 개념의 연장이며 이는 1915년 아인슈타인의 상대성 이론에서 시작되며 그 후 1950~1960 년대에 들어 구체적 이론이 정립된다.
드리고 싶은 말씀은 슈바르츠실트가 논문을 쓰던 1916년에는 1915년에 나온 아인슈타인의 상대성 이론을 근거로 한 중력장 개념만 있었을 뿐 구체적인 블랙홀 개념은 없었으며, Black Hole 이란 단어조차 생겨나지 않았다는 것이다. Black Hole 단어가 정식으로 사용되기 시작한 것은 1964년 또는 1967 년으로 인정되고 있다. 따라서 중력장 (Gravitational Field) 개념이 시작된 1915년 이후 1967 년까지 블랙홀이란 “개념” 은 특정한 명칭 없이 부르는 사람 마음대로 Collapsed Star, Frozen Star 또는 Vacuum Star 등으로 불렸다 한다.
그러면 블랙홀이란 단어는 누가 처음 만들어 냈는지 알아 보겠다. 미국의 저널리스트인 Ann Ewing 이란 사람이 1964년 1월 18일에 American Association for the Advancement of Science (미국 과학발전협회) 에 제출한 보고서 제목 <Black Hole in Space> 에 Black Hole 이란 단어가 처음으로 나타난다고 한다. 그러나 여기서의 Black Hole 이 지금 우리가 말하는 블랙홀인지는 더 이상 자세한 기록을 찾을 수 없었다.
위의 보고서와는 별도로 과학계에서 일반적으로 사용되기 시작한 연도는 1967 년이다. 미국의 이론 물리학자인 John Archibald Wheeler (존 휠러 1911~2008) 가 어떤 강연회에서 지금의 블랙홀의 개념을 표현하기 위해 사용했으며 이 때부터 이 단어가 일반적으로 사용되었다고 한다. 이런 이유로 블랙홀이란 말은 John Archibald Wheeler 가 창안한 단어라고 일반적으로 인정된다. . 그러나 당사자인 Wheeler 는 자기가 처음 사용한 사람은 아니라고 평생 우겼다는데, 아마도 Ann Ewing을 염두에 둔 말인지도 모를 일이다.
따라서 1916년 슈바르츠실트가 전쟁 중에 생각해낸 이론은 결코 <어떤 천체가 “블랙홀” 이 되기 위한 반지름> 은 아니었고 이는 나중에 그의 본래 이론이 <가공> 된 결과물이다. 예를 들면 아인슈타인이 E = m c ² 란 공식을 고안해낼 때 원자폭탄을 만들겠다는 생각은 없었다는 것과 같다. 천문학, 물리학 교양서적들을 보면 때로는 독자를 쉽게 이해시키는데 너무 중점을 두기 때문에 이론의 본질이 왜곡되는 것을 가끔 보아와서 한 말씀 드려보았다.
(3) 수학문제 만드는 사람, 그 문제 푸는 사람
1915년에 발표된 아인슈타인의 상대성이론의 근간은 <중력>에 관련된 사항이었고, 이는 유명한 아인슈타인의 <중력장 방정식 (Equation of Gravitational Field) >으로 표현된다. 1687년 Newton 의 Principia 가 나왔을 때 이 책에 나온 내용을 이해하는 과학자가 별로 없었던 것처럼, 당시 아인슈타인의 중력장 방정식도 아인슈타인이 만들기는 했지만 당시 완전히 이해하는 과학자도 별로 없는 난해한 수학공식이었다. 사실 아인슈타인 그 자신도 그것에서 파생될 어마어마한 진실은 당시 그 자신도 모르고 있었을 것이다.
그러나 이론물리학은 실험과 관측으로 증명되어야만 진리로 인정된다. 이 방정식에 따르면 빛이 중력에 의해 휘어야지만 방정식이 맞다고 증명이 된다. 아인슈타인은 머리도 좋지만 운도 좋은지 불과 4년후인 1919년에 영국 물리학자 Arthur Eddington 이 개기일식 때 태양 주위를 지나는 빛이 휜다는 사실을 관측해서 아인슈타인을 하루아침에 슈퍼스타로 만들어 주었다.
중력렌즈 효과를 Einstein’s Ring 이라고 부르고, 또는 유명한 Quasar 인 G2237+0305 의 별칭이
Einstein’s Cross 인 것은 모두 그의 중력장 방정식 때문이다. 아래는 Einstein’s Cross 인데 가운데 보이는 은하의 중력 때문에 그 보다 멀리 있는 한 개의 별 (Quasar) 이 지구에서 볼 때 네 개로 중복되어 보인다.

<Einstein’s Cross (G 2237+0305) 지구에서 거리 80 억 광년>
그런데 1916년 1차 대전에 참전해있던 같은 독일의 슈바르츠실트가 아인슈타인의 논문을 읽고 바로 그 다음해인 1916년에 <일정조건> 인 경우 아인슈타인의 중력장 방정식의 해답 (Solution) 을 풀어냈다. 그 <일정조건> 이란
<회전하지 않는 천체인 경우> 를 말하며, 그가 유도한 해답의 <일부> 가 이 바로 이번 칼럼의 소재인 슈바르츠실트 반지름 공식이다. 달리 말하면 <슈바르츠실트 반지름>이란 <회전하지 않는 천체의 중력장 방정식> 에서 파생된 결과의 일부이며 그 것은 아인슈타인 중력장 방정식을 풀어낸 해답이다.
(4) 슈바르츠실트 반지름 공식 구하기
1. 자전하지 않는 천체인 경우
위에선 말씀 드린대로 슈바르츠실트 반지름이란 회전하지 않는 어떤 천체 표면에서의 <탈출속도가 빛의 속도에
도달> 하려면 그 천체의 부피가 얼마가 되어야 하는지에 대한 것이다. 그러면 탈출속도 = 빛의 속도라는 등식이 갖는 의미를 좀 더 알아보겠다.
지난호 Serial No 11 에서 아인슈타인의 E=mc ² 공식 이전에 이미 E=mv ² 라는 공식이 있었고, 이는 Gottfried Wilhelm Leibniz (라이프니츠, 1646~1716), Émilie du Châtelet (샤틀레, 1706~1749), Willem Jacob 's Gravesande (스흐라베잔데 1688~1742) 의 연구 덕분이라고 말씀 드렸다.
어떤 물체가 최대한의 에너지를 갖기 위해선 물체의 질량 m 이 정해져 있다면, E=mv ² 에 따라
속도 v 를 최대한 높이는 것이다. 그런데 우주에서의 속도는 광속 c 를 초과할 수 없으므로 mc ² 가 최대의 에너지가 될 것이다.
같은 이치로 어떤 천체에서의 탈출속도도 계속 증가할 수는 있으나 그 속도가 빛의 속도에 이르면 더 이상 증가할 수 없을 것이고 탈출속도가 빛의 속도보다 크다면 그 천체표면에선 아무것도 빠져나올 수 없을 것이다. 이유는 우주에서 빛보다 더 빠른 것은 없기 때문이다. 그런데 어떤 천체의 중력이 너무 커서 “빛 조차 빠져 나오지 못하는 천체” 를 바로 블랙홀이라 한다. 이는 “블랙홀에선 탈출속도가 빛의 속도보다 크다” 는 말과 같다.
이처럼 <어떤 천체에서 탈출속도가 “빛의 속도에 도달” 하려면, 즉 블랙홀이 되려면 “천체의 질량이 그대로 유지될 경우에” 그 천체의 부피, 즉 반지름이 얼마가 되어야, 또는 얼마까지 줄어야 하는지에 대한 계산> 이 바로 슈바르츠실트 반지름이다.
따라서 탈출속도 공식이나 슈바르츠실트 반지름 공식이나 모두 같은 어머니를 가진 형제들이며 동전의 앞 뒷면과 같다. 슈바르츠실트 반지름을 이해하려면 탈출속도에 대한 이해가 선행되어야 한다고 생각되어 위 칼럼에서 탈출속도를 먼저 언급 드렸다.
탈출속도 공식의 기본 전제조건 중에 하나가 천체가 자전하지 않는 것인 것과 같이 슈바르츠실트 반지름 공식도 자전하지 않는 천체가 조건이다. 따라서 이 식에서 도출되는 블렉홀도 <자전하지 않는 블랙홀> 이란 가정임에 유의하시기 바란다. 탈출속도 칼럼에서 언급 드린 자전하지 않는 천체표면에서의 빛의 속도인 최대 탈출속도는 다음과 같다.
V = (2 GM / r ) 1/2 또는
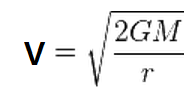
V 탈출속도
G 중력상수 : 6.67384 x 10−11 m3 kg -1 sec -2
M 지구질량 : 5.9736 x 10 24 kg
r 지구중심에서 물체중심까지 거리 :
물체가 작고, 지구표면에 있다는 가정이므로 지구반지름과 같다.
지구평균 반지름 6,371 km
c 빛의 속도 299,792,458 m/s
탈출속도 V 가 빛의 속도인 c 가 되어야 하므로 V 를 c 로 치환하면
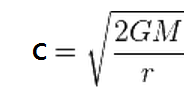
양변 제곱하고 정리하면
r = 2 GM / c 2 또는
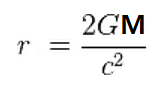
위의 식이 <슈바르츠실트 반지름 공식> 이다
2. 태양 및 행성들이 블랙홀이 될 경우의 크기 구하기
그러면 지구표면 탈출속도가 빛의 속도인 경우 지구 반지름부터 구해본다.
다른 말로는 지구가 블랙홀이 될 경우 지구의 반지름이다.
다만 자전하지 않는 블랙홀이란 가정임을 기억하시면 된다.
r = 2 GM / c 2 에 위에 명기한 수치를 대입하면
r = 2 x (6.67384 x 10−11 m3 kg -1 sec -2 ) x 5.9736 x 10 24 kg / (299,792,458 m/s)²
= 8.8715 x 10 -3 meter
= 반지름 0.88715 cm (약 0.89 cm), 지름 약 1.77 cm
따라서 지구 반지름이 약 0.89 cm, 지름이 약 1.77 cm 가 되면 지구도 블랙홀이 된다. 다만 자전하지 않는 블랙홀인 경우이다. 문제는 지금까지 발견된 우주의 모든 블랙홀은 모두 자전하고 있으므로 다소 비현실적인 전제조건일 것이다.
하여간 자전하지 않는 블랙홀이 되는 경우, 아래 천체들이 블랙홀이 되기 위한 지름 (반지름이 아님) 을 계산하면 아래와 같다. 크기를 상상해 보시는데는 반지름 보다 지름이 더 용이할 것 같아 지름으로 표시했다.
천 체 지 름 천 체 지 름 (반지름이 아님)
--------------------------------------------------------------------------------
지 구 1.77 cm 목 성 5 m 63.8 cm
수 성 0.098 cm 토 성 1 m 68 cm
금 성 1.446 cm 천왕성 25.8 cm
화 성 0.19 cm 해왕성 30.4 cm
태 양 5 km 900 m (5.9 x 103 m)
우리은하 전체 약 0.4 광년
(4.16 x 1015 m, 1 광년 = 약 9.46 x 1015 m)
----------------------------------------------------------------------------------
3. 자전하는 천체인 경우
그런데 대부분의 항성이나 행성, 블랙홀은 자전한다. 만일 자전하는 천체라면 위의 탈츨속도 칼럼에서 간단히 알아본 것처럼 중력장 수치도 변화할 것이다. 1916년에 슈바르츠실트가 아인슈타인의 중력장 방정식으로부터 “자전하지 않는” 천체인 경우의 해답을 발표한 때로부터 47년이 지난 1963 년에 와서야 New Zealand 의 수학자 Roy Kerr (1934 ~ 현재 생존) 란 분이 “자전하는” 천체인 경우의 중력장 방정식 해답을 고안해냈다.

<Roy Kerr (1934~현재 생존) 사진 Univ. of Canterbury>
사실 과학계도 시대에 따라 인기 있는 연구분야가 있다. 세계의 모든 물리학자가 47년 동안 그 해답을 구하려 했으나 실패한 것은 아니고, 1920년대 이후 중력장 분야 인기가 시들해지다가 1950~1960년대 들어 블랙홀이 인기를 얻기 시작하자 다시 연구 성과가 나오기 시작했다고 보아야 한다. 그러면 천체 물리학에서 최근에 인기 있는 분야는 ? 아마도 미시적으론 입자물리학에 관련된 양자역학이고, 거시적으론 암흑물질 및 암흑에너지 분야가 아닐까 한다.
하여간 Roy Kerr 커가 연구한 자전하는 천체의 중력장 방정식에서 도출된 블랙홀 개념을 나중에 <Rotating Black Hole (자전하는 블랙홀)> 또는 Kerr 블랙홀이라 부르게 되었고, 슈바르츠실트의 중력장 해답에서 유래한 블랙홀을 Non-Rotating Black Hole (자전하지 않는 블랙홀) 또는 Schwarzschild 블랙홀 이라고 부르게 된다.
Roy Kerr 의 계산에 따르면 어떤 자전하는 천체가 블랙홀이 된다면, 그 크기는 평균적으로 슈바르츠실트 반지름 공식으로 계산한 수치의 1/2 정도가 된다. Roy Kerr 수치 계산은 저의 한계를 한참 초과하므로 생략한다.
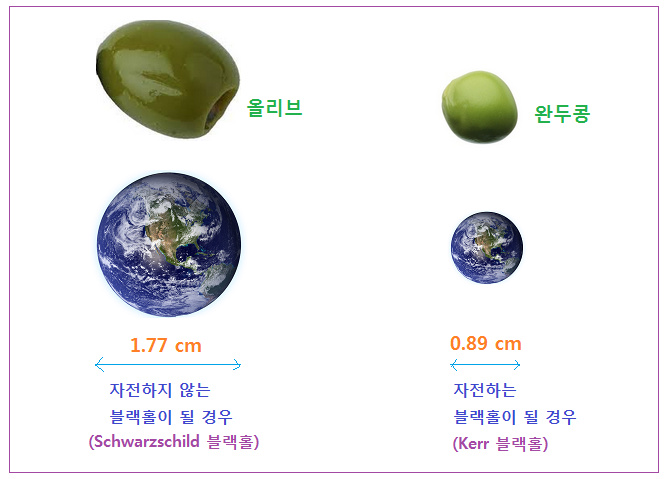
<Schwarzschild 블랙홀, Kerr 블랙홀이 될 경우 지구의 크기를 올리브와 완두콩으로 비교한 것>
위의 그림은 지구가 Schwarzschild 블랙홀 과 Kerr 블랙홀이 될 경우의 크기를 제가 좋아하는 올리브 열매와 완두콩 크기로 비교한 것이다. 좋아하시는 것에 따라 대추 또는 포도 알갱이든 메추리 알이든 무엇으로든 비교하시면 기억하기 쉬우실 것이다.
지구 평균반지름이 6,371 km 이므로 지름은 12,742 km 가 될 것이다. 지구가 자전하지 않는 경우, 탈출속도가 빛의 속도에 도달해서 블랙홀이 되려면 12,742 km 지름이 1.77 cm 가 되어야 한다. 더욱이 만일 지구가 자전하는 블랙홀이 된다면 지름이 1 cm 도 안되는 0.89 cm 가 된다니, 제 머리로는 접근이 안된다. 그러나 우둔한 제 머리로 접근 불가한 것이 어디 “지구 블랙홀” 뿐이랴. 요즘에는 사무실 관상수 가지에서 매일 조금씩 빠져 나오는 연초록 빛 어린 나뭇잎 생명력 조차 신비할 따름이다.
III. Surprise & Mystery
새롭게 밝혀진 우리은하 모습
(1) 2005년 나선에서 막대나선으로 수정된 우리은하
사람이란 원래 이웃집 젓가락 갯수는 알아도 자기집 국그릇 금 간 것은 모르고 사는 존재인 것 같다. 사실 평생 자기 얼굴은 직접 보지 못하고 죽을 때까지 남의 얼굴들만 보고 살아야 하기 때문인지도 모른다. 잠시 생명이 멎어 사망한 상태까지 갔다가 다시 살아 돌아오는 현상인 근사체험 (近死體驗) 한 사람들은 생명이 멎었던 그 순간, 영혼이 육신을 이탈해서 자기 얼굴을 보았다던데 증명할 길은 단 하나밖에 없으니 정말인지 궁금하다.
우주의 모습을 담은 수많은 사진들 중에서 우리은하 원반 모습을 온전히 담은 것은 없다. 우리 은하 밖으로 나가지 않는 이상 있을 수 없는 일이다. 그러면 다른 방법으로 우리은하 구조와 모양을 추정해야 하는데, 사실 은하 내부에서 전체 구조를 알아내는 일은 쉽지 않은 문제이다. 그러나 세상살이 모두 그렇듯이 방법이 없는 것은 아니다. 여기서는 <어떤 방법> 으로 우리은하 구조를 탐색하는지 알아보고 최근인 2013년에 새롭게 발표된 <우리은하의 구조와 모습> 을 알아보려 한다.
우리은하 구조를 알기 위해서는 은하내부 수많은 천체들간의 정확한 거리 측정해야 한다. 수십 만개 천체들을 다루어야 하므로 시간과 끈기의 싸움이다. 우선 천체간 거리를 줄자로 잴 수는 없으므로 쓸만한 망원경이 있어야 한다. 우리은하 구조연구에 제일 먼저 동원된 망원경은 2003년 8월에 발사된 Spitzer 우주 망원경 (Spitzer Space Telescope) 이다.

<Spitzer Space Telescope 조립 모습>
수십년 동안 우리은하는 단순한 나선은하 (Spiral Galaxy)로 생각되었다. 그러나 1990년대 들어 나선은하가 아닐 수도 있다는 여러 가지 연구결과가 나오기 시작했다. 2003년 미국 Wisconsin 대학교의 Ed Churchwell 과 Robert Benjamin 두 분이 우리은하 구조에 대해 그 때 발사된 Spitzer 우주 망원경을 사용해서 본격적으로 연구하게 되었는데, 드디어 2005년에 우리은하가 실제론 <막대나선 은하 (Barred Spiral Galaxy)> 라는 놀라운 증거들이 발견되었다. 따라서 2005년 이후에 나온 책이나 자료들에선 우리은하가 막대나선 은하로 수정되어 있다.
(2) 직경이 하와이부터 대서양까지인 전파망원경 VLBA
Spitzer 우주 망원경은 Ritchey-Chrétien 식이다. 비록 우주에서 관측하지만 보다 정확한 은하지도를 만들려면 전파망원경이 효율적일 수 있다. 따라서 2008 년부터는 VLBA (Very Long Baseline Array)> 라는 전파망원경이 우리은하 지도를 만드는데 동원되었다
이 망원경은 원격조정되는 직경 25m의 접시형 전파망원경 10개로 이루어져 있는데, 한 곳에 모여있는 것이 아니고, 아래 그림처럼 하와이부터 미국 대륙과 중미에 걸쳐 퍼져있다. 원격조정 Center 는 아래 지도에서 4번 위치인 New Mexico 주 Socorro 의 Pie Town 이다.
따라서 이 전파망원경 각각의 직경은 25 m 에 불과하지만 실제 성능은 직경이 1번 하와이부터 10번 US Virgin Islands 까지 거리인 망원경이 된다. 광학 망원경은 지역적으로 떨어져 있어도 결코 서로 연결될 수 없다. 구경이 지배하는 망원경 사회에서 전파망원경 장점 중의 하나가 이것이다. 최근에는 유럽, 러시아, 미국의 전파망원경을 연결해서 직경이 지구크기인 전파망원경도 이용한다고 들었다.
아래 그림은 VLBA 각각의 전파망원경 모습과 설치된 위치를 표시한 그림이다. 위치는 접시안테나가 너무 커서
알아보기 힘들므로 별도로 지도에 그려서 표시해 드렸다.

<VLBA 각각의 전파망원경 모습과 대략적인 위치. 자료: 원치복 서울지부장님/ habrahabr.ru>
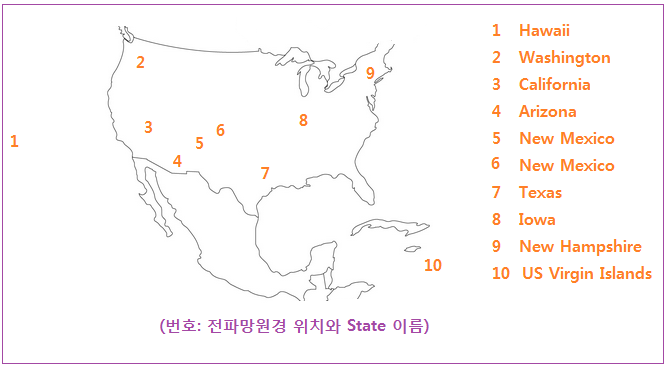
<VLBA (Very Long Baseline Array) 전파망원경 위치>
(3) 삼각측량이란 ?
지금도 토목공사에서 정확한 거리를 잴 때는 삼각측량법 (Trigonometry) 을 사용한다. 이것은 두 지점 사이 거리를 미리 알고 있고, 그 두 지점에서 거리를 알고 싶은 위치까지의 방향과 각도를 잰 후 삼각함수를 이용해서 그 위치까지의 거리를 측정하는 방법이다. 그리이스 시대의 천재 탈레스 (BC 624~545) 가 처음으로 삼각측량 방법을 사용해서 이집트 피라미드 높이를 계산했다고 전해진다.
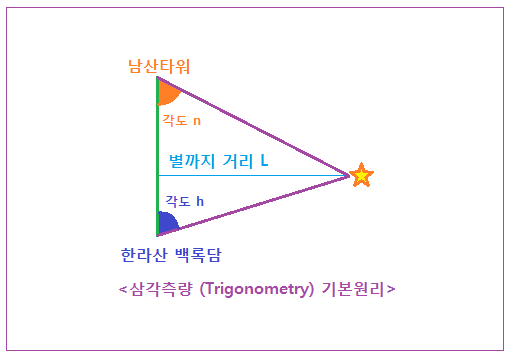
<삼각측량 (Trigonometry) 기본원리>
위 그림에서 남산타워와 한라산 백록담 사이의 정확한 거리를 알고 있다면, 각각의 지점에서 어떤 별까지의 각도 n 과 h 를 재면 그 별까지 거리 L 을 계산할 수 있다. 거리를 구하는 삼각함수 내용은 생략한다.
(4) 시차 (Parallax) 를 이용한 별까지 거리측정
1. 연주시차와 Parsec (파섹) 단위
그런데 별은 너무 먼 거리에 있으므로 남산에서 방향과 각도를 재나, 한라산 꼭대기에 가서 재나 별을 향한 방향과 각도 차이를 알기는 불가능하다. 심지어 지구 북극점과 남극점에서 측정해도 차이를 알 수 없을 것이다. 따라서 별까지의 방향과 각도를 잴 때 남산타워와 한라산 백록담 사이의 거리처럼 미리 알고 있어야 하는 두 지점 사이 거리가 클수록 차이가 많이 날 것이다. 그러면 지구에 사는 사람이 가장 멀리 이동할 수 있는 방법은 ?
그 해답은 역설적이게도 <움직이지 않고 가만히 앉아 때를 기다리는 것> 이다. 그 “때” 란 정확히 6 개월 후 같은 시간이다. 6 개월 후 같은 시간에는 지구가 태양을 180 ° 돌아서 반대편에 가 있으므로 사람은 가만히 앉아서도 299,195,741,400 m (약 3억 km) 를 이동한 것이 된다.
하루에 164 만 km 씩 달린 셈…. 때로는 설치지 않고 조용히 때를 기다리는 것도 사는 방법 중 하나이다.
참고로 1 AU 는 149,597,870,700 m 이므로 이 거리의 두배가 지구가 태양 반대편으로 갔을 때의 지구의 이동 거리이다.
지구는 태양을 1년에 한 번 공전하므로 예를 들어 봄에 한 번 각도를 재고, 6개월 후 가을에 지구가 180 ° 반대편으로 갔을 때 각도를 재면 별까지의 각도도 가장 클 것이고 그 거리도 지구의 태양 공전궤도 지름이므로 이미 정확히 알고 있는 것이 된다. 이런 방법을 <연주시차 (Annual Parallax)> 측정이라 부른다.
아래 그림으로 간단히 설명 드린다. 다만 위의 삼각측량 그림에서 측정하는 각도는 n 과 h 인데 반해서 <연주시차는 각도 p> 이며, 또한 양쪽 지구에서 보이는 각도가 아니라 태양과 지구 사이의 각도임에 유의하시면 된다. 따라서 양쪽 지구에서 보이는 각도의 반이 연주시차이다.
실제 측정할 때는 각도 a 를 구하고 반으로 나눈다.
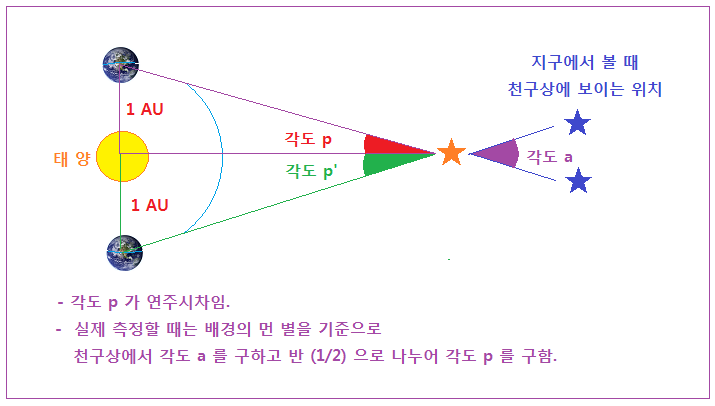
<연주시차 개념>
연주시차가 1” (초각, arcsecond) 일 때 지구에서 별까지의 거리를 1 Parsec 단위로 정한다.
Parsec 이란 말은 PARALLAX OF ARCSECOND (초각 시차) 란 말에서 굵은 글자만 따서 만든것이다.
1 Parsec 거리를 정확히 측정해보니 3.26156 광년임이 밝혀졌다. 정리하면 아래와 같다.
Parsec 단위
= PARALLAX OF ARCSECOND 의 약자
= 연주시차가 1” (초각, arcsecond) 인 경우의 거리
= 3.26156 광년
그러나 별까지 거리를 재는 여러 방법 중에서 연주시차는 시차가 너무 미세해서 측정이 어렵고 지구대기로 인한 오차도 생겨서 100 pcs이상 거리에 있는 천체에는 잘 사용되지 않는다. 태양에서 4.22~4.24 광년 떨어진 가장 가까운 별인 Proxima Centauri의 연주시차도 겨우 0.76” (초각) 이라고 한다.
그러나 전파망원경은 광학망원경에 비교되지 않을 만큼 정확하고, 더욱이 VLBA 전파망원경은 Hawaii 에서 US Virgin Islands 에 걸쳐 10개나 되므로 대단히 미세한 시차까지 측정할 수 있다.
우리은하 내부의 별들은 지구에서 멀어야 10~12만 광년이므로 VLBA 가 가장 적합한 연구수단이 된 것이다. VLBA 는 2008년부터 우리은하 구조를 탐색하는 Project 를 시작했는데, 2012년 말에 연구를 종료하고 최근 2013년에 그 동안의 연구결과를 발표했다
2. 연주시차 측정경쟁 우승자 Bessel
여기서 잠시 연주시차를 사용해서 별까지 거리를 처음 측정한 사람에 대해 알아보고 지나가겠다.
인류가 연주시차란 개념은 오래 전부터 알고 있어 왔으나 그것을 이용해서 별까지 거리를 측정하고자 했던 때는 1830년대 들어서이다.
당시 많은 천문학자들이 연주시차 측정에 매달렸으나 그 크기가 너무 작아 모두 실패하고 1838년에 와서 독일의 Friedrich Wilhelm Bessel (1784~1846) 이란 분이 드디어 측정에 성공했다. 대상 별은 백조자리 61번별 (61 Cygni) 이었는데 당시 측정치는 0.314” (초각, arcsecond) 이었다. 이로 인해 Bessell 은 졸지에 유명해지고, 나중에는 달의 맑음의 바다 (Mare Serenitatis. Sea of Serenity) 에 있는 Crater 에도 이름이 올라가게 되었다.


<Friedrich Wilhelm Bessel 초상> <달의 Bessel Crater.
Serial No 3 에 올렸던 사진을 다시 인용>
(5) 2005~2012년까지 생각되던 우리은하 구조
아시다시피 우리은하는 막대나선은하 (Barred Spiral Galaxy) 이며 여러 개의 나선팔 (Spiral Arm) 이 막대모양의 은하 중심부에서 뻗어 나온다. 우리 태양계가 위치한 나선팔은 우리가 그곳에 존재한다는 뜻에서 Local Arm (국부 나선팔) 이라고 부른다.
VLBA 의 연구결과가 나오기 전인 작년 2012년까지는 Local Arm 이 대형 나선팔인 Sagittarius Arm 에서 나뭇가지처럼 삐져 나와서 Sagittarius Arm 과 그 이웃 대형 나선팔 Perseus Arm 사이에 그리 길지 낳은 거리로 뻗어있다고 생각되었다. 따라서 Arm 이라고도 사용하지만 Sagittarius Arm 에서 삐져 나온 나뭇가지라는 의미에서 주로 <Spur> 라고 불렸다. Spur 란 영어는 <Spur Track> 등으로 사용되는데, 이는 간선철도에서 삐져나와 출발선만 간선철도에 연결되어 있고 종착역은 끊겨있는 철도의 지선 (支線) 을 말한다.
한편 우리 태양계에서 비교적 가깝고 세계적으로 유명한 별들은 Orion Belt 의 세 별과 Orion 성운이다. 따라서 <Local Arm> 의 이름을 <Orion Arm> 또는 <Orion Spur> 라고 불러왔다.
아래 그림은 2012 년까지의 연구결과를 토대로 만들어진 우리은하구조 모델이다. 각 나선팔들의
이름은 2013년 새로이 발표된 은하구조를 말씀 드릴 때 언급 드리려 한다.
그림을 보시면 Sagittarius Arm 에서 왼쪽으로 삐져 나온 소규모 나선팔이 보인다. 아시는 바와 같이서 은하중심에서 태양까지 거리는 26,000 광년이고, 우리은하 직경은 12만 광년이다.
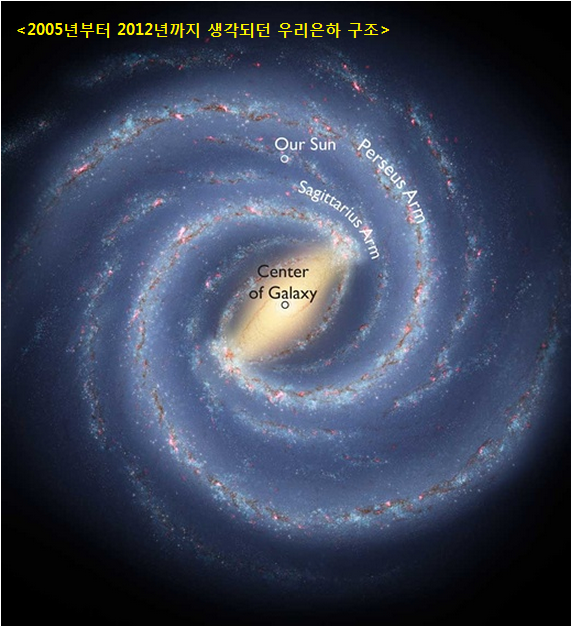
<2005~2012년 까지 생각되던 우리은하 구조. 아래 출처 그림에 일부 추가.
그림 Robert Hurt, IPAC/Bill Saxton, NARO/AUI/NSF/NASA/Astronomy>
Serial No 12 에서 올려 드린 그림을 아래에 다시 보여 드린다. 태양 주변을 묘사한 것으로, 위의 그림에서 “Our Sun” 부분을 확대한 것으로 생각하시면 될 듯하다. 북극성 (Polaris) 도 이웃이고 거대한 Betelgeuse 도 빨간 점으로만 보인다. Orion Belt 와 Orion 성운도 지척에 있다. 그러나 게 성운 (Crab Nerbula) 은 길 건너편 동네인 Perseus Arm 에 사는 것이 보인다. 하여간 아래 그림 보시면 우리가 속한 Local Arm 을 왜 Orion Spur 또는 Orion Arm 이라 부르는지 짐작하실 수 있을 것이다.

<Orion Spur 또는 Orion Arm 과 태양계 주변. 그림 Richard Powell>
(6) 2013년에 새롭게 밝혀진 우리은하 구조
그런데 VLBA 가 2008년부터 4년이 넘는 기간 동안 수많은 별들까지 거리를 측정한 결과, 우리가 사는 Local Arm (= Orion Spur = Orion Arm) 은 위의 그림처럼 Sagittarius Arm 에서 삐져 나온 것이 아니라 <Perseus Arm> 에서 갈라져 나왔으며, 더욱이 소규모 나선팔이 아니라 어느 정도 규모가 있는 중형 나선팔 이었음이 새롭게 밝혀졌다. 추가로 Perseus Arm 및 은하 외곽을 돌고 있는 Outer Arm 내부에서 별이 만들어지는 지역의 상세한 정보도 같이 알게 되었다.
금년에 새롭게 밝혀진 구조는 아래 그림과 같다. Local Arm 이라고 써있는 부분을 위의 2005~2012년에 생각되던 은하구조 그림과 비교해 보십시오. 이전 그림에서 Local Arm 은 Sagittarius Arm 에서 삐져 나온 소규모 나선팔로 묘사되어 있지만, 아래 그림에선 Local Arm 이 Perseus Arm 에서 갈라져 나왔고 규모 또한 많이 커진 것으로 그려져 있다. 이제는 Local Arm 을 <Spur> 라고 부를 수 없게 되었고 명실상부하게 <Orion Arm> 이란 독립된 이름을 붙인다고 한다.

<2013 년에 새롭게 밝혀진 우리은하 구조. 아래 출처 그림에 일부 추가.
그림 Robert Hurt, IPAC/Bill Saxton, NARO/AUI/NSF/NASA/Astronomy>
아래 그림은 위 그림에 나선팔 이름을 붙인 것이다. 한편 나선팔 이름은 이전에는 각각의 나선팔에 좀 복잡하게 붙어 있었으나 2013년 모델에는 나선팔들 위치가 다소 수정 되면서 이름들이 통합된 것들이 있다. 아래에 예를 들어본다.
Sagittarius Arm = Carina – Sagittarius Arm
Centaurus Arm = Scutum – Centaurus Arm
Orion Arm = Orion – Cygnus Arm
하여간 우리 태양계가 있는 Local Arm 은 Orion Spur 또는 Orion Arm 이라 불러왔으나 2013년부터는 Orion-Cygnus Arm 이라는 이름으로도 부른다는 것만 참고하시고 다른 것들은 일견만 하셔도 될 듯하다.
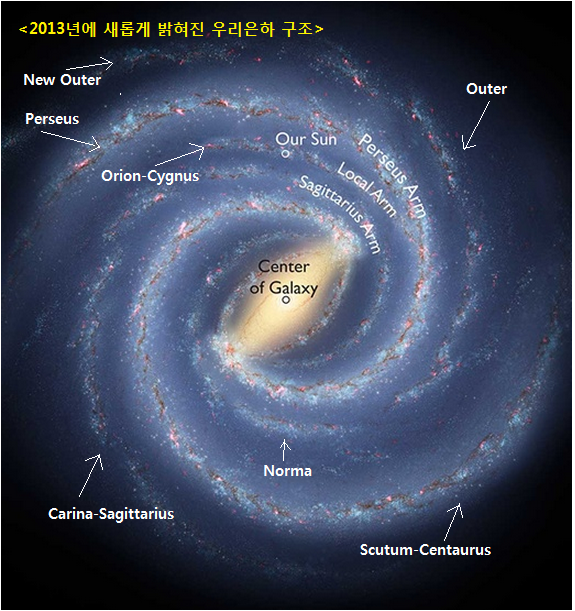
<2013 년에 새롭게 밝혀진 우리은하 구조에 나선팔 이름 추가.
아래 출처 그림에 일부 추가.
그림 Robert Hurt, IPAC/Bill Saxton, NARO/AUI/NSF/NASA/Astronomy>
(7) 아프리카 초원에서 만납시다
그런데 가만히 생각해보니 우리 태양계의 고향인 Local Arm 의 뿌리가 얼마 전까지만 해도 Sagittarius Arm 이었으나 금년 들어 졸지에 그 뿌리가 Perseus Arm 으로 바뀌어 버렸다. 우리 전통관습으로 말하면 본관 (本貫) 이 사지타리우스 자리 팔의 <士芝 (사지)> 씨에서 페르세우스 자리 팔의 <陛露 (폐로)> 씨로 바뀐 것으로 볼 수 있다.
제가 만들어본 본관에 굳이 뜻을 붙이자면, “士芝 (사지)” 는 “선비 같은 품격의 향기로운 버섯” 이라 할 수 있다.
“陛露 (폐로)” 에서 “陛” 는 건물 앞의 신발 벗어놓는 디딤돌이 원래 뜻이며, 건물 앞에 깔아 놓은 평평한 돌들도 "폐" 라 한다. "폐하" 란 말에 쓰이는 글자이다. 이 한자는 고대 진시황이 "황제" 호칭을 사용한 이후로 중국에서 신하들이 황제를 부를 때 사용했는데, 신 같이 높은 황제를 더 높여 부를 수 없으니, 부르는 사람을 낮추어 "황제가 업무 보는 건물 바깥의 신발 놓는 디딤돌에 서서 황제를 부른다" 는 뜻이다.
그러나 TV 사극에서 보셨듯이 조선시대 임금님 호칭은 "폐하" 가 아니고 "殿下 (전하)" 이다. 여기서 "殿" 은 "전각" 의 줄인 말로 황제보다 한 단계 낮은 "왕" 이 일하는 건물이다. 진시황의 진나라 이후로 "왕" 이란 정치적으로는 중국에 종속되어 있지만 다스리는 영토 내에서는 독립된 통치권한을 가진 지배자를 의미해왔다. 또한 비록 통치하는 영토는 없더라도 황제의 아들이나 동생들에게도 왕의 호칭을 주었다.
참고로 서열만으로 본다면 황제의 동생보다는 황제의 아들이 높은 법이다. 따라서 황제의 아들을 "친자식" 이란 말처럼 특별히 "친왕 (親王)" 으로 불렀다. 고종이 황제로 즉위한 후 그 아들에 대한 호칭인 "영친왕, 의친왕 " 을 기억하실 것이다. 여기서 영 (英) 및 의 (義) 는 이름이 아니고 왕에 붙인 시호이다. 그러면 왕의 아들에 대한 호칭은 ?
세종대왕이 즉위 전에 충령대군이었던 것은 잘 아실 것이다. 왕 아들이나 동생은 "君" 으로 불렀다. 한편, 박정희 대통령이 좋아했다는 호칭 "閣下 (각하)" 의 "閣" 은 관료가 업무 보는 관청 건물이다. 장관들 조직을 "內閣 (내각)" 으로 부른다.
우리 조선시대에는 고종 때 중국의 간섭을 배제하고 자기들 마음대로 조선을 주무르려는 일본의 정략에 의해 황제로 즉위한 것을 빼고는 모두 황제보다 한단계 아래인 "왕" 직함을 쓸 수 밖에 없었다. 호칭도 "황제의 궁궐보다 한 단계 아래인 전각에 사는 사람" 이란 뜻인 "전하" 로 불러왔다. 왕이나 왕세자가 정해지면 중국에서 "책봉" 을 받아야했고... 자존심 상하는 역사가 아닐 수 없다. 어찌보면 관청에서 일하는 사람이란 뜻인 "각하" 란 호칭이 더 소박하고 진솔해 보이기까지 한다. 물론 나중에는 이 각하의 일하는 방향이 바뀌어 많은 분들이 고통받기도 했다. 나라가 강하고 잘 사는 것이 제일 중요하지만 진실된 역사를 알아야 미래 역사의 발전이 가능하다고 믿는다.
페르세우스 자리 팔의 "陛露 " 문중이란 의미를 설명 드리려다 삼천포 다녀왔다. 하여간 여기서 "폐로" 는 최고로 높여 부르는 호칭처럼 “이슬 중에서 최고로 아름다운 이슬” 의 뜻을 표현하려 했다.
어쨌거나 그동안 “사지” 문중에서 갈라진 집안이라고 믿어왔던 태양으로선 좀 황당하리라 생각된다. 그러나 “사지” 문중이든, “폐로” 문중이든 무엇이 중요하랴. 지금 현재의 태양 모습 보다 중요한 것은 없으리라 믿는다. 더욱이 우주적인 관점에서 본다면 모든 나선팔이 우리은하 안에서 태어난 자손들이므로 어떤 <Arm> 출신인지 구분하는 것조차 의미 없으리라 생각한다.
사실 우리 사람들도 길게 보면 모두 아프리카 동부 나무 위에서 놀다가 초원으로 내려온 유인원의 자손들이다. 우리나라도 삼국시대 초기에 유래한 일부 성씨들을 제외하고는 대다수 민중들의 성씨는 하대신라 말기부터 고려 초기에 생겼다. 그 이전엔 사회 구성원 대부분은 성씨가 없었다고 보아야 한다. 그러면 삼국시대 초기 일부 성씨 및 저를 포함해서 고려 이후에 갖게 된 성씨 모두 어디서 오셨을까 ? 결국 올라가다 보면 모두 아프리카 동부 초원에서 만나게 되리라 믿는다. 예전엔 모두 같이 모여 털 속의 벼룩 잡아주던 조상들… 앞으론 모두 더욱 사랑하는 마음을 가져야 되겠다.
IV. Coffee Break
무궁화시움 (Mugunghwacium), 원소번호 119, 기호 Mm ? ?
(1) 재미있는 원소이름 – 우라늄, 플루토늄의 어원
“금, 이는 듣기만 하여도 기분 좋은 금속이다”. 지난번 인용한 수필가의 말은 좀 바꾸어 금 (金
Gold) 을 표현해 보았다. 세상에 금 드린다고 하면 싫어하는 사람 있을까 ? 물론 의심 많은 세상이기 때문에 그냥 드린다 해도 다른 엄청난 대가를 요구할까 봐 겁나서 안받아 가시는 분도
많으실 듯하다. 금이란 녹슬지 않는 금속이기 때문이기도 하지만 그 오묘하고 아름다운 빛깔 때문에 인류문명이 생긴 이래로 사랑 받아왔고 세계 경제제도의 기반이 되는 금속이기도 하다.
그러나 많은 분 손가락 반지에 있는 금은 우주 저편 머나먼 곳에서 지구까지 찾아온 귀하신 손님이다.
우리는 철 (원소번호 26 / 원소기호 Fe / 원소이름 Iron) 과 그보다 가벼운 원소는 우주에 존재하는 항성들 내부의 핵융합으로 만들어졌고, 철보다 무거운 원소는 초신성 폭발로 만들어진다고 배웠다. 우리 몸도 철을 포함해서 그 보다 가볍고 무거운 수많은 원소들로 이루어져 있으므로 우리 자신을 “별 부스러기” 또는 “우주로부터 온 물질” 이라 부르기도 한다. 철보다 무거운 원소를 철 다음부터 몇 개만 열거해 본다.
-----------------------------------------------------------------------
코발트 27 Co Cobalt 텅스텐 74 W Tungsten
니켈 28 Ni Nickel 백금 78 Pt Platinum
구리 29 Cu Copper 금 79 Au Gold
아연 30 Zn Zinc 납 82 Pb Lead
은 47 Ag Silver 우라늄 92 U Uranium
-------------------------------------------------------------------------
우주에서 자연적으로 만들어진 원소는 위 표에서 원소기호 순서로 92번 우라늄이 마지막이다.
그러나 핵폭탄 원료인 플루토늄 같은 원소는 우주에서 자연적으로는 만들어지지 않으며 실험실에서 사람이 만든 원소이다. 핵폭탄 문제가 이슈가 될 때마다 플루토늄을 얼마나 많이 “추출” 했는지 언론에서 떠드는 이유가 바로 사람이 만들어 “추출” 해내는 원소이기 때문이다.
그러면 <우라늄> 이나 <플루토늄> 의 어원은 무엇일까 한 번 생각해 보시지요. 다른 원소 말고 특히 우라늄과 플루토늄의 어원을 알아보는 이유는 그 어원이 <천문학> 과 관련이 있기 때문이다. 또한 <넵튜니움> 이란 원소도 있다. 여기까지 말씀 드리면 답이 생각나실 것이다.
이 세가지 원소 이름의 어원은 태양계 행성이며 답은 다음과 같다.
원소이름 영어이름 영어어원 우리말 어원 (원소번호/원소기호)
-------------------------------------------------------------------------------
우라늄 Uranium Uranus 천왕성 (92 / U )
넵튜니움 Neptunium Neptune 해왕성 (93 / Np)
플루토늄 Plutonium Pluto 명왕성 (94 / Pu)
--------------------------------------------------------------------------------
(2) 아인슈타니움도 있다
아래에서 열거 드리는 원소기호 93번 (넵튜니움) 이후로는 모두 사람이 인공적으로 만들어낸 원소들이다. 태양계 행성 이름들이 어원이면 유명한 과학자 이름도 빠질 수 없을 것이다.
제일 먼저 생각나는 분은 아인슈타인. 이 분 이름의 원소도 있을까 ? 과학자 이름이 어원인 원소들 몇 개 보시지요.
원소이름 영어이름 영어어원 (원소번호/원소기호)
-----------------------------------------------------------------------------------
아인슈타니움 Einsteinium Albert Einstein (99 / Es)
퀴리움 Curium Marie Curie (96 / Cm)
페르미니움 Fermium Enrico Fermi (100 / Fm)
노벨리움 Nobelium Alfred Nobel (102 / No)
코페르니시움 Copernicium Nicolas Copernicus (112 / Cn)
------------------------------------------------------------------------------------
원소가 만들어진 지역 이름을 딴 것도 있다.
원소이름 영어이름 영어어원 (원소번호/원소기호)
-----------------------------------------------------------------------------------
아메리시움 Americium America 대륙 (95 / Am )
버클리움 Berkelium Berkeley 도시 (97 / Bk)
캘리포니움 Californium California 주 (98 / Cf)
-----------------------------------------------------------------------------------
인공적으로 만든 원소의 마지막은 Ununoctium (유너녹티움) 이란 원소인데, 원소기호 Uuo, 원소번호 118번이다. 이것의 어원은 새로 만들어진 원소를 관리하는 International Union of Pure & Applied Chemistry (국제 순수 및 응용화학 연맹, IUPAC) 의 관리체계에 따라 작명되었다 한다.
앞으로 새로이 명명될 119 번 원소는 “Mugunghwacium – 무궁화시움 – 원소기호 Mm ” 이 되기를 기대해본다.
V. Journey to Deep Sky
잃어버린 별자리를 찾아서 (8 회)
Rangifer 또는 Tarandus – 순록자리
당분간 Journey to Deep Sky 공간에 <잃어버린 별자리를 찾아서> 칼럼을 연재합니다.
(1) “순록” 이란 한자어에 대하여
예전 별자리에 사슴인 순록자리가 있었음을 알고 나서 <순록> 이란 단어에 대해 잠시 생각해 보았다. <록> 은 한자로 사슴을 뜻하는 말임을 알지만 <순> 자는 무슨 의미인지 도통 감을 잡을 수가 없었다. 성질이 “온순” 한 사슴인지, 아니면 ”순수” 혈통 사슴인지…
한자 사전 찾아보니 “순록” 을 <馴鹿> 으로 쓰고 있었다. 여기서 <馴> 자는 제가 모르는 한자라서 사전을 다시 찾기 전에 그 뜻을 한 번 생각해 보았다. 말 (馬) 옆에 시냇물 (川) 이 있으니
“시냇물에서 목욕하는 말” 인가 ? 그러면 “ 鹿 (사슴)” 과는 무슨 관계인지 ? <馴> 자 뜻을 찾아보니 “길들일 순” 이라 한다. 이것을 보고 비로소 그 뜻을 알게 되었다. 한자는 두개 글자가 붙어 있을 때 서로 의미를 보충하기도 하지만 어떤 경우에는 한 글자는 “의미” 를 나타내고 나머지 글자는 “발음” 을 표시한다.
<馴> 자의 경우, <馬> 는 “의미”를 나타내는 요소이고 <川> 자는 “발음” 을 표시한다고 생각된다. <川> 의 우리말 발음은 “천” 이지만 다른 글자와 같이 쓰이면 <順> 글자처럼 “순” 으로도 발음된다. “의미”를 나타내는 <馬> 는 제 추정상 “말 (馬) 처럼 길들여서 타고 다니는 것” 을 의미하는 것 같다. 따라서 순록은 "말처럼 길들여서 타고 다니는 사슴" 의 뜻이 된다. 실제로 에스키모 등 원주민들은 순록을 “길들여서” “말” 처럼 타고 다닌다. 이 칼럼 쓰면서
사실 제가 스스로 배우는 것이 많다

<순록도 “길들여서” “말” 처럼 타고 다닌다. 그림 indigosociety.com>
(2) 산타클로스와 루돌프 사슴도 별자리에 있으면 좋을 듯
1. 산타클로스 출생기원
우리나라에서 제일 큰 명절은 아무래도 설날과 추석이다. 그러면 서양에선 어떨까 ? 제 생각으론 아마도 추수감사절과 크리스마스가 아닐까 한다. 그런데 지금 우리가 아는 밤하늘 별자리 88 개는 서양 및 중동에서 고대 문명이 생길 때부터 만들어진 것이 대부분이므로 그 지역 문화가 많이 반영되어 있다. 크리스마스가 서양에서 제일 큰 명절 중 하나이므로 산타클로스 또는 그의 썰매를 끄는 사슴도 별자리에 들어가 있을 법한데 지금 별자리에는 왜 없는지 궁금해서 제 나름대로 그 이유를 찾아 보았다.
산타클로스 기원에 대한 믿을만한 가설에 따르면 지금의 Turkey 인 Lycia (리시아) 지역의 Myra (미라) 도시에 살던 대주교의 영국 표기 이름인 Saint Nicholas (성 니콜라스. AD 270~343) 에서 유래했다고 한다.

<Saint Nicholas 초상. 18세기 러시아 그림>
영국어 Saint Nicholas 를 독일에선 Sankt Nokolaus, 프랑스에선 Saint Nicolas, 네덜란드, 벨기에 등에선 Sint Nikolaas 로 썼다. 그런데 초창기 미국으로 이주한 네덜란드 인들은 Sint Nikolaas 를 간단히 줄여서 <Sinterkaas> 로 사용했고, 이 말이 미국어로 정착되면서 Santa Claus 가 되었다는 가설이다.
그러나 노르웨이, 스웨덴, 덴마크 핀란드 등 여러 북유럽 국가들이 모두 그럴 듯한 이유를 들어 산타클로스가 자기들 국가에서 유래했다고 주장하고 있으므로 어느 것이 맞는 가설인지 알 길이 없다. 또한 특이한 산타클로스 모자와 복장도 18 세기부터 Saint Nicholas 를 표현한 그림에 유사하게 나타나지만 지금의 모습처럼 빨간색 모자와 옷으로 정형화 한 것은 1931년 코카콜라 광고가 시초라 한다.
2. 루돌프 사슴 출생기원
한편 루돌프 사슴을 설마 연약한 꽃사슴 이라고는 생각하지 않으시리라 믿는다. 어느 누구도 푸들이나 차와와에게 썰매를 끌게 하지 않는 것과 같다. 혹시 영화 “The Polar Express” 를 보셨는지요 ? 아래 그림은 이 영화에 나오는 싼타클로스와 사슴인데 분명히 꽃사슴은 아니다. 이 사슴은 <순록> 인데 영어로는 <Reindeer> 라 부르며 북유럽과 시베리아에 서식한다.
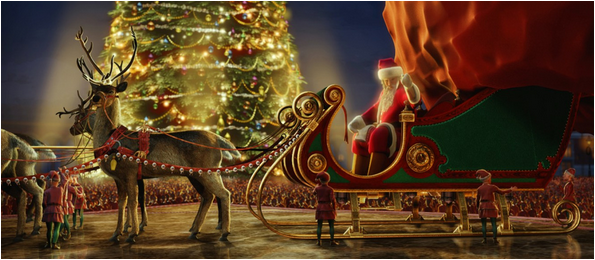
<영화 The Polar Express 에 나오는 싼타 할아버지의 사슴. 사진 carnegiesciencecenter.org>

<Reindeer. 그림 dimensionsinfo.com>
그런데 Canada , Alaska, Greenland 등에 서식하는 순록 종류는 별도로 <Caribou>라 부른다.
아래는 Caribou 사진과 두 종류 순록의 서식지를 표시한 지도이다.

<Caribou. 그림 dinosoria.com>
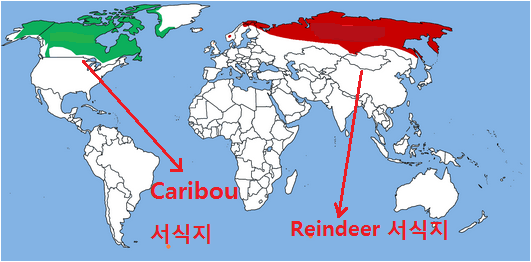
<Caribou 와 Reindeer 서식지 >
그러면 루돌프 사슴은 언제부터 유래했는지 알아보자. 루돌프 사슴은 미국의 백화점 체인점인
Mongomery Ward 가 광고를 위해 1939 년에 Robert L. May 에 의뢰해서 만든 동요 (Verse) 에서 유래되었다. 당시 동요 제목은 <Rudolph, the Red-Nosed Reindeer> 였다. 따라서 루돌프 사슴 종류는 순록으로 처음부터 정해져 있었다. 이 동요는 곧이어 어린이를 위한 이야기 책으로도 출판되어 많은 인기를 끌었다 한다. 아래는 1939년에 출판된 책 표지이다.

<1939 년 출판된 Robert L. May 의 책 표지. “루돌프, 빨간 코의 순록”>
루돌프 사슴을 만든 Robert L. May 가 이 순록을 Caribou라 하지 않고 Reindeer 라고 부른 이유는 Santa Claus 고향을 눈이 많이 내리는 북유럽이라고 생각했기 때문일 것이다. 그러면 루돌프 사슴은 암놈일까요 ? 숫놈일까요 ? 정답은 숫놈입니다. 제가 직접 성별을 구분해 본 것은 아니고 Robert L. May 가 지은 동요 및 책에 숫놈으로 되어있다고 한다. 위 그림에서도 맨 앞의 순록 머리에 뿔이 조금 난 것을 볼 수 있다.
그리고 산타클로스 썰매를 쓰는 순록은 몇 마리인지 세어 보십시오. 모두 9 마리입니다. 이것도 Robert L. May 의 동요에 그렇게 써 있다고 한다. 싼타 할아버지가 9 마리 중에서 제일 나이 어리고 빨간 코가 빛나는 루돌프를 예뻐해서 썰매 맨 앞에 서게 했다는 이야기….
정리해보면, 산타클로스의 실제 인물인 Saint Nicholas 는 AD 270~343 에 살았으나, 하얀 수염에 빨간 옷을 입은 모습은 1931년 코카콜라 광고에 처음 등장했고, 순록인 Rudolph 는 1939년 Mongomery Ward 백화점 광고에 처음 등장한 것이다.
그런데 지금의 88개 별자리는 1928년에 Eugéne Delporte 가 이끄는 위원회가 정리한 것을 1930년에 IAU 가 승인한 것이다. (Serial No 13 참조) 따라서 1928년에 88개 별자리가 정리되고 나서 3년 후인 1931 에 등장한 지금의 산타클로스 모습이나, 11년 후에야 백화점 광고에 나타난 루돌프 사슴이 별자리에 올라갈 수 없던 것은 당연할 것이다.
(3) 순록이 별자리에 오르게 된 사연
1. 순록과 측지학 (Geodesy) 의 이상한 관계
순록은 위의 서식지 지도에서 보신 것처럼 툰드라 지대나 북극권에 살기 때문에 중위도 지역에 사는 사람들은 동물원 아니면 순록을 평생 구경조차 할 수 없는 동물이다. 이렇게 보기 어려운 동물이 어떻게 별자리까지 오를 수 있었을까 ? 순록의 밤하늘 등극은 측지학 (Geodesy) 이라는 , 동물과는 전혀 관계없는 과학 덕분이다. 측지학이란 지구 표면의 형상을 구하기 위해 지구 각 지점의 위치, 높이, 거리 등을 측정하는 학문이다.
순록자리는 프랑스 천문학자 Pierre-Charles Le Monnier (피에르 샤를 르모니에 1715~1799) 가
1743년에 출판한 책 La Théoie des Comètes (혜성에 대한 이론) 에서 이 별자리를 처음으로 만들어 올려 놓았다. 이 분은 지난 호 Serual No 19 의 같은 칼럼에서 언급 드린 <Turdus Solitarius (지빠귀 자리)> 를 만든 사람이다. 순록자리가 생긴 사연을 알아보기 위해서 당시 지구 모양에 대한 유럽 과학계 논쟁을 동향을 잠시 살펴본다.
당시 지구가 타원모양인 것은 모두가 인정하고 있었으나, 어떤 타원인지를 놓고 두 개 이론이 대립하고 있었다. 프랑스의 수학자 Pierre-Louis Moreau de Maupertuis (모뻬르뚜위 1698~1759) 는 적도 방향이 볼록한 타원 (Oblate Shperoid) 이라 주장했고, 같은 프랑스 천문학자 Jacque Cassini (자끄 카시니 1677~1756) 는 자전축 방향이 볼록 (Prolate Spheroid) 하다고 주장했다.
참고로 여기서 나오는 Jacque Cassini 는 토성 고리 카시니 간극이라든가, 달 Carter 이름 및 토성 탐사 위성 등에 나오는 Giovanni Domenico Cassini (1625~1712 ) 의 아들이다. 아버지 도메니코 카니시는 원래 Italy 출생인데 파리천문대 건립에 초빙되어 일하면서 프랑스 이주했고, 따라서 아들 자끄 카시니는 프랑스 국적이 되었다. .
하여간 지구가 어떤 타원인지 알려면 적도지역의 위도 1 ° 간의 거리와 북극이나 남극지역의 위도 1 ° 간의 거리를 정확히 측량해서 비교하면 된다. 이것은 달리 말하면 지구의 <편평도 (Oblateness)> 를 측정하는 것인데, 편평도란 어떤 천체가 공 모양의 구체인지 타원체인지 그 찌그러진 정도를 말한다. 그런데 당시 적도지역은 상세한 탐사가 이루어져 있었으나 극지방은 접근이 어려워 탐사가 이루어지지 않고 있었다.
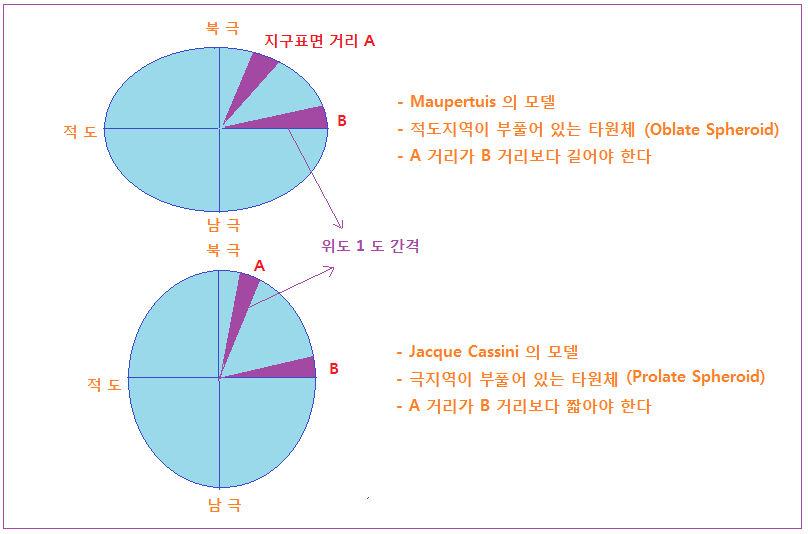
<지구 타원체에 대한 Maupertuis 와 Jacque Cassini 의 논쟁>
1736년에 프랑스 국왕 Louis XV (루이 15세) 는 38세의 Maupertuis 를 단장으로 하는 탐사단을
1년 기간을 주고 Lapland 지역으로 파견했다. 이 지역은 지금의 노르웨이, 스웨덴, 핀란드 북부인데, 아래의 Lapland 지도 보시면 탐사의 어려움이 짐작되실 것이다.
당시 나이로 21세에 불과한 Le Monnier 도 이 탐사단의 일원으로 파견된다. 젊은 나이에 국왕이 조직한 탐사단 일원이 되었으니 당시 프랑스에선 촉망 받던 청년 천문학자였던 것 같다. 그는 Serial No 19 에서 언급드린 것처럼 46세 중년에는 금성일면 통과 관측을 위해 아프리카 동부 인도양에 있는 Rodrigues Island 방문 후 동남아를 여행했다.
Maupertuis 탐사단의 Lapland 지역의 위도 1 ° 거리 측량결과, 적도지역보다 더 긴 것으로 나타나서 지구 편평도 논쟁에서 Jacque Cassini 에게 KO 승을 거두었다. Le Monnier 는 이 탐사에서 보게 된 Reindeer 순록에 깊은 감명을 받은 것 같고, 1737년 귀국 후 6 년이 지난 다음에 출판한 책에 순록자리를 만들어 올렸다. 따라서 순록의 별자리 등극은 결국 측지학, 지구 편평도 측정의 덕분이라고 보아야 할 것이다.
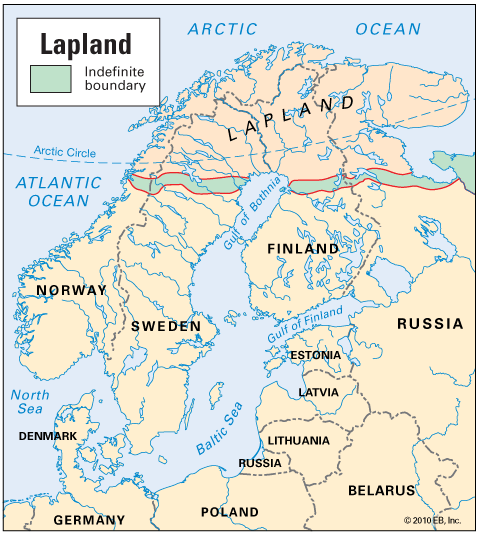
<Lapland 지역. 그림 kids.britannica.com>
2. Rangifer 와 Tarandus 의 차이
그러면 이 순록은 어디에 자리 잡았는지 성도 먼저 살펴 보겠다. 북극권에 사니까 당연히 북극 부근에 집을 마련해 주었을 것이다. 또한 그 순록 종류도 Caribou 가 아니라 Le Monnier 가 Lapland 지역에서 본 Reindeer 일 것이다.
아래 성도에서 순록이 작아 찾기 어려우실 것 같아 성도 축소판에 붉은 원 표시해서 먼저 올려 드린다. 그 아래 큰 그림에서 사슴 모양을 찾아 보십시오. 사슴 옆에 잘 보이지 않는 작은 글자는 <Tarandus> 이다.
<순록자리 위치 표시 – Tarandus>
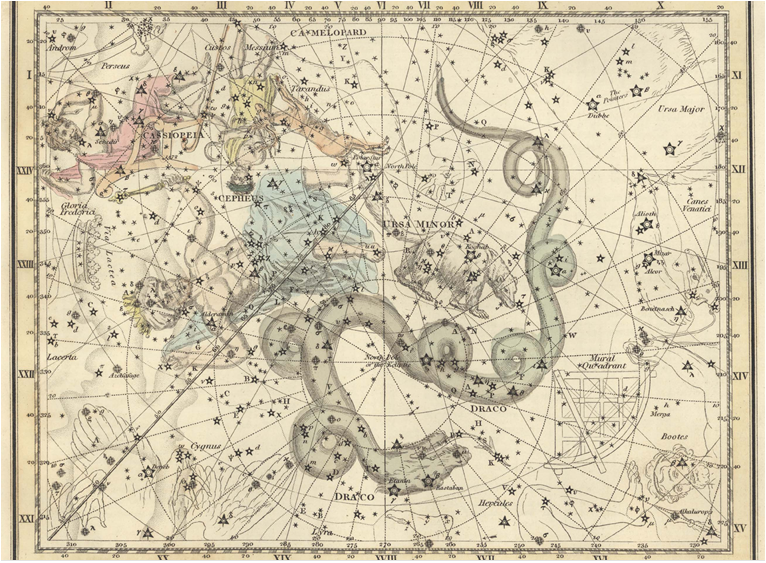
<Alexander Jamieson 의 성도 Celestial Atlas 1822년>
Reindeer 의 라틴어는 <Rangifer> 또는 <Tarandus> 이며, 이 두가지 이름 모두 쓰인다. 다만 Tarandus 는 Reindeer 의 종명 (種名 Specific name) 이고, Rangifer 는 속명 (屬名 Generic name) 이라고 한다. 생물을 분류할 때 작은 범위부터 큰 범위까지의 명칭은 다음과 같다. 저도 참고 삼아 알아두려고 열거해 보았다.
종 à 속 à 과 à 목 à 강 à 문 동물 / 식물 à 계
種 à 屬 à 科 à 目 à 綱 à 門 동물 / 식물 à 界
Species à Genus à Family à Order à Class à Phylum / Division à Kingdom
(4) 별자리 순록의 녹생여정 (鹿生旅程)
Le Monnier 가 1743년에 출판한 책 La Théoie des Comètes 에는 별자리 이름이 <Le Réene> 로 되어 있으며, 프랑스어로 순록이란 말이다. 한편 1776년에 그의 동료인 Jean Fortin 이란 사람이 만든 성도 Atlas Céleste 에도 같은 이름으로 표기되어 있다.
그러나 1801년에 Johann Bode 는 Uranographia 를 출간하면서 이 별자리는 그대로 살려 놓았으나 Le Réene 라는 프랑스어 별자리 이름을 라틴어인 Rangifer 로 바꾸어 올렸다. 그 후 1822년 영국인 Alexander Jamieson 이 1822년 Celestial Atlas 를 발행할 때는 같은 뜻의 라틴어 Tarandus 로 다시 바꾸어 올린다. 아마도 Bode 의 성도를 따라 했다는 말은 듣기 싫어서 그런지도 모르겠다. Jamieson 의 성도는 위에 올려 드렸고, 아래에 Bode 의 Uranographia 에 실린 순록자리를 보여 드린다.
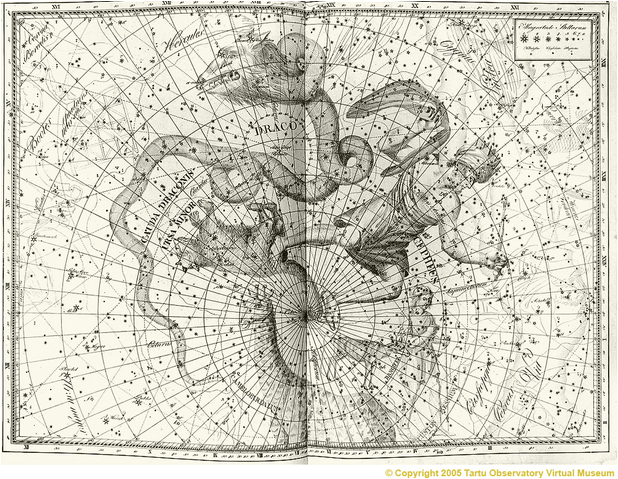
<Bode 의 1801년 Uranographia 에 실린 순록자리 (Ranfiger).
오른쪽 페이지 아래 부분. 그림 air.ee>
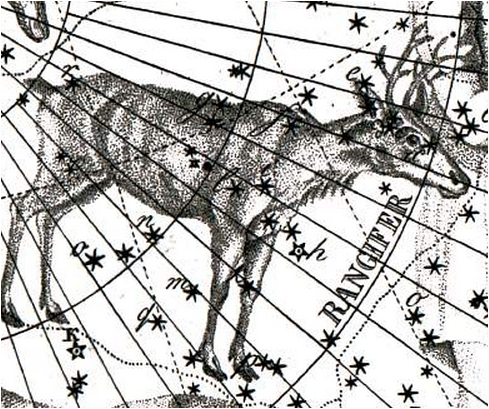
<위의 그림 부분 확대. 그림 ianridpath.com>
이 순록은 1928년에 결국 밤하늘에서 사라진다. Le Monnier 에 의해 1743년 출생해서 Deporte 에 의해 1928년 사망했으니 무려 185 년을 살았다. 역시 사슴은 영물이라 그런지 살기도 오래 산다.
Deporte 가 순록을 퇴출시킨 이유는 아마도 개인업적을 기념하는 별자리라 그런지도 모를 일이다. 다만 파리도 날아다니고 도마뱀도 기어 다니는 밤하늘에 늠름한 순록 한 마리쯤 있으면 더 좋았을 것으로 생각된다. 루돌프 사슴이 어른 된 것으로 보아도 좋을 것이고. 이 별자리 위치를 현재 성도에 표시해 드리면서 이 칼럼 마무리 드린다. 기린자리 (Camelopardalis) 와 카시오페이아 자리 (Cassiopeia) 사이에 있다.
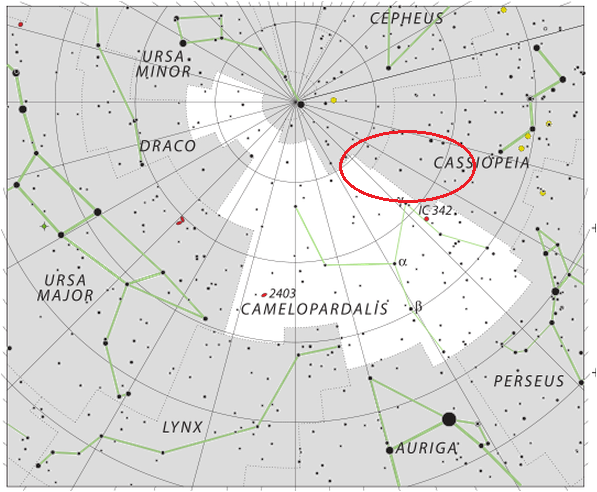
<순록자리 (Rangifer 또는 Tarandus) 위치. 붉은 색 원표시. 성도 Sky & Telescopes>
VI. Moon River Wider Than a Mile
Hyginus Crater 와 계곡
난 얻어맞고 생긴 것 아니거든 !
(1) 이열치열 – 더위는 증기사우나로 이긴다
요즘 날씨가 더위 먹었는지 연일 최고기온을 갈아 치운다. 지구가 정말로 뜨거워지는가 보다. 산이 높으면 골이 깊고, 달도 차면 기우는 법인데, 이러다 어떤 영화처럼 자고 일어나니 갑자기 창문 밖에 빙하기가 와 있는 건 아닌지 걱정된다. 저는 사우나를 좋아하는데 건식보다는 습식, 특히 증기 사우나를 좋아한다. 이열치열 (以熱治熱) 이란 말도 있으니 증기사우나 생각하시라고 달의 <증기의 바다>에 있는 요상한 지형 하나 소개해 드리려 한다.
<증기의 바다> 는 라틴어로 Mare Vaporum 이라고 쓰며 영어로는 Sea of Vapours 이다. 바다를 표현하는 좋은 단어들도 많은데 왜 하필 “증기” 라는 말을 썼는지 알다가도 모를 일이다. 바다가 끓어서 증기가 생길 수 있나 ? 아니면 바다안개 (海霧) 를 표현한 것인지 ? 이상한 바다 이름이 이것만은 아니다. <뱀의 바다>도 그 중의 하나. 이 바다는 라틴어로 Mare Anguis 로 쓰고 영어로는 Sea of Serpent 이다. 그 바다엔 바다뱀들이 우글거리나보다.
도대체 어떤 사람이 달에 증기의 바다라는 이상한 이름을 갖다 붙였는지 찾아 보았더니 Italy 의 신부이며 천문학자였던 Giovanni Battista Riccioli (1598~1671) 라는 분이라 한다. 이 분은 지구의 자전, 공전연구 및 달지도 제작 등 업적이 있다.

<Giovanni Battista Riccioli (1598~1671) 초상 그림 sundiahouse.it>
(2) 계곡인지 도랑인지 – 히기누스 계곡
증기의 바다는 비의 바다 (Mare Imbrium, Sea of rain) 와 맑음의 바다 (Mare Serenitatis, Sea of Serenity) 사이에 있는데, 좁은 틈에 비집고 들어가있는 모습이 좀 궁색해 보인다. 규모도 다른 대형 바다들과는 작아서 직경이 245 km 에 불과하다. 그러나 그 나이는 늦게 잡아도 38 억년 정도 되므로 다른 바다들에 비해 오래된 편이다. 그러나 여기서는 증기의 바다 자체를 알아보는 것은 아니므로 이 정도로만 알아보고 오늘의 주인공으로 넘어가겠다.

<증기의 바다 주변. 노란색 사각형>
우선 달에서 어느 부분을 밀씀 드리고 있는지 그 위치부터 알려 드리는 것이 순서일 것이다. 위의 달지도에서 노란색 사각형이 오늘 말씀 드리고 있는 동네이다. 사각형 가운데 검은 부분이 증기의 바다이고 그 왼쪽 큰 바다가 비의 바다, 오른쪽이 맑음의 바다이다.

<위의 노란색 사각형 부분 확대. 달지도 원치복 서울지부장님>
위 지도는 노란색 사각형 부분 확대한 것이다. 증기의 바다 아래쪽에 <히기누스 계곡> 이란 표시가 있는데, <히> 글자의 위쪽의 가느다란 선이 히기누스 계곡 이다. 그러나 <곡> 글자 오른쪽의 가느다란 선은 다른 이름의 계곡
이다. 이 가느다란 선 이름은 아리아데우스 계곡 (Rima Ariadaeus) 인데, 아래에 올리는 채색한 지도에선
좀 더 자세히 보인다. 하여간 이것들은 사실 “계곡” 이라 부르기 민망할 정도라 “도랑” 으로 부르고 싶다.
한편 히기누스 글자 중간 쯤에 <히기누스 Crater> 라는 작은 Carter 가 있는데, 글자와 겹쳐 있어 위 지도에선 보이지 않는다. <히기누스> 지형의 영어 (라틴어) 명칭을 아래에 정리 드린다. 여기서는 <히기누스 Crater> 및 <히기누스 계곡> 으로 사용하겠다.
히기누스 Crater : Hyginus Crater
히기누스 계곡 : Rima Hyginus 또는 Hyginus Rille
아래 두 사진은 이 부분을 확대 및 근접촬영한 것이다.

<히기누스 Crater 와 계곡. 사진 Wes Higgins>

<히기누스 Crater 와 계곡의 LROC 사진.
LROC : Lunar Reconnaissance Orbitor Camera >
위 사진들에서 중간부분의 활 모양으로 뻗은 계곡이 히기누스 계곡이고, 그 중간 부분에 다소 큰 원형과 그 곳 위에 붙어 있는 작은 원형 Crater 가 히기누스 Crater 이다. 히기누스 계곡은 사진 오른쪽으로도 계속 연장되어 그 길이가 220 km 에 달한다. 히기누스 Crater 직경은 11 km 이고
깊이는 800 m 정도이다.
(3) 달 앞면에서 3개 밖에 없는 지형 – 히기누스 Crater
그러면 히기누스 Crater 모양을 자세히 보십시오. 이 Crater 주변에 보이는 다른 여러 Crater 들은 전형적인 사발모양인데 반해서 히기누스 Crater 는 내부가 평평한 쟁반 모양이다 더욱이 다른 Crater 들은 외곽 Rim 이 분명히 보이지만 히기누스 Crater 는 달 표면에 원통형 물체를 꾹 눌러 놓은 것 같은 모습이다. 어떻게 이런 희한한 모양이 생겼을까 ?
이유는 히기누스 Crater 는 결코 <충돌 Crater> 가 아니고 달 표면의 화산활동으로 생긴 <Caldera (칼데라)> 이기 때문이다. 따라서 엄밀히 말하면 <히기누스 Crater> 가 아니고
<히기누스 Caldera> 로 불러야 맞을 것이다. 그러나 망원경이 발명된 이후 달지도가 만들어지면서부터 Crater 로 부르던 관습에 따라 아직도 Crater 로 부르고 있다. 히기누스 계곡도 마찬가지로 충돌로 형성된 것이 아니고 달 표면이 함몰되어 생긴 지형이다.
그러면 달에서 이런 Caldera 는 얼마나 될까 ? 달 앞면 전체를 뒤져 보아도 진짜 Caldera 는 <히기누스 Caldera> 를 포함해서 3개에 불과하다. 그러나 달탐사 궤도위성이 근접사진을 찍어 보내기 전에는 3개 정도가 더 있다고 생각되었으나 정밀사진 분석결과 그 3개는 Caldera 가 아닌 것으로 밝혀졌다. 아래에 진짜 Caldera 와 나중에 Crater 로 밝혀진 것들을 정리했다.
실제로 Caldera 인 것 예전엔 Caldera 로 생각되었으나
최근 Carter 로 밝혀진 것
-------------------------------------------------------------------------------------------
Hyginus (직경 11 km) Vitello (직경 42 km)
Crüger (ü 대문자는 Ü. 직경 45 km) Ritter (직경 29 km)
Ina (직경 36 km) Sabine (직경 30 km)
--------------------------------------------------------------------------------------------
아래 두 그림은 지형을 잘 알아볼 수 있도록 채색한 것이다. 흑백사진 보다는 히기누스 계곡이 연장되는 부분이 잘 보인다. 바로 아래 그림에 주변부 지형 이름을 추가해 드렸다.

<채색한 달지도. 히기누스 계곡 주변부. Android lunar map>
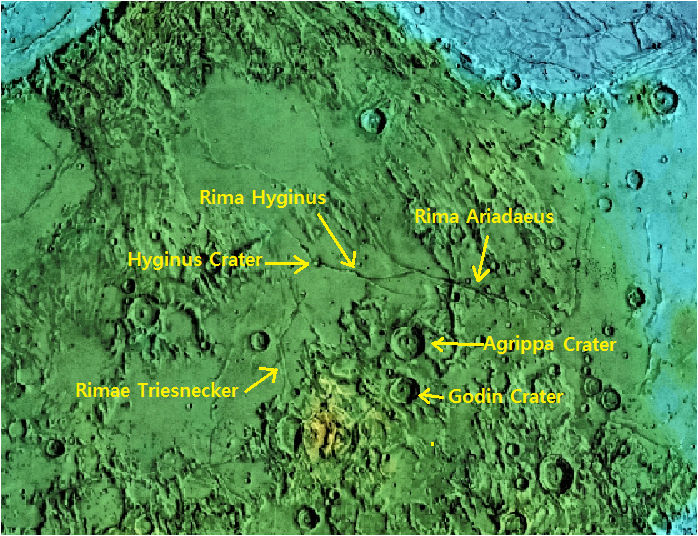
<위의 지도에 지형이름 추가>
그러면 히기누스는 어떤 분의 이름일까 ? 이 분의 본명은 Gaius Julius Hyginus (BC 64~AD 17) 이다. 로마 제정초기 Augustus 황제의 노예였는데 머리가 명석하고 학문을 좋아해서 Augustus 황제가 자유민으로 만들어 주었다고 한다. 이 분은 천문학에 조예가 깊었다고하며 Poeticon Astronomicon 또는 De Astronomia (천문학) 이라 불리는 책을 저술했다고 전해진다.
참고로 Apollo 13호를 제외하곤 11호부터 17호까지 모두 달 착륙에 성공했다. 그런데 실제로 Apollo 18, 19, 20호도 계획에 있었으나 승무원들이 훈련하던 도중에 Apollo 계획이 취소되었다.
1970년에 발표된 NASA 보고서 Scientific Rationale Summeries for Apollo Candidate Lunar Exploration Landing Sites 에 따르면 <히기누스 계곡> 은 Apollo 19호 또는 20호의 착륙장소 후보로 되어있다. Apollo 19호 착륙장소로는 Hadley Rille 도 후보지였는데, 이곳은 Apollo 15호가 먼저 착륙장소로 사용했다.
만일 Apollo 계획이 20호까지 진행되었다면 19호나 20호 둘 중의 하나는 히기누스 계곡에 착륙했을 것이고 히기누스 계곡 및 Crater 도 유명해졌을 것이다. 비록 규모로는 다른 대형 계곡이나 Crater 와는 비교할 수 없지만, 히기누스 Crater 는 셀 수도 없을 만큼 많은 달의 Crater 중에서
3 개 밖에 없는 것 중의 하나이니 그 희귀성으로도 존중 받아야 할 듯하다.
<드리는 말씀>
Astro News 를 시작한 후 이번호가 Serial No 20 이니 벌써 스무번 칼럼을
올린 것이 됩니다. 첫 회를 작년 2012년 2월 6일 올렸으니 1년 6개월이
지났습니다. 사실 시작할 당시에는 내용이 알차거나 유익한 정도는 차치하고,
얼마나 오랫동안 지속할 수 있을지 저 스스로도 확신이 없었습니다.
빈약한 내용과 허접한 잡문에 불과한 글일지라고 오늘까지 계속할 수 있던 것은
여러 회원님들의 격려와 지원 덕분입니다. 20 회 지면을 빌어서 다시 한번
진심으로 감사인사 올립니다. 앞으로 내용을 개선해가면서 힘 닿는데까지 열심히
연재하겠습니다. 회원님들의 지속적인 관심 부탁 드립니다.
Astro News <끝>






 Astro News - Serial No 21 - Sep 2013
Astro News - Serial No 21 - Sep 2013
 Astro News - Serial No 19 - July 2013
Astro News - Serial No 19 - July 2013

무더운 여름 20번째 연재를 해주셨네요. 항상 감사드립니다. 좋은 내용 천천히 읽어 보겠습니다.